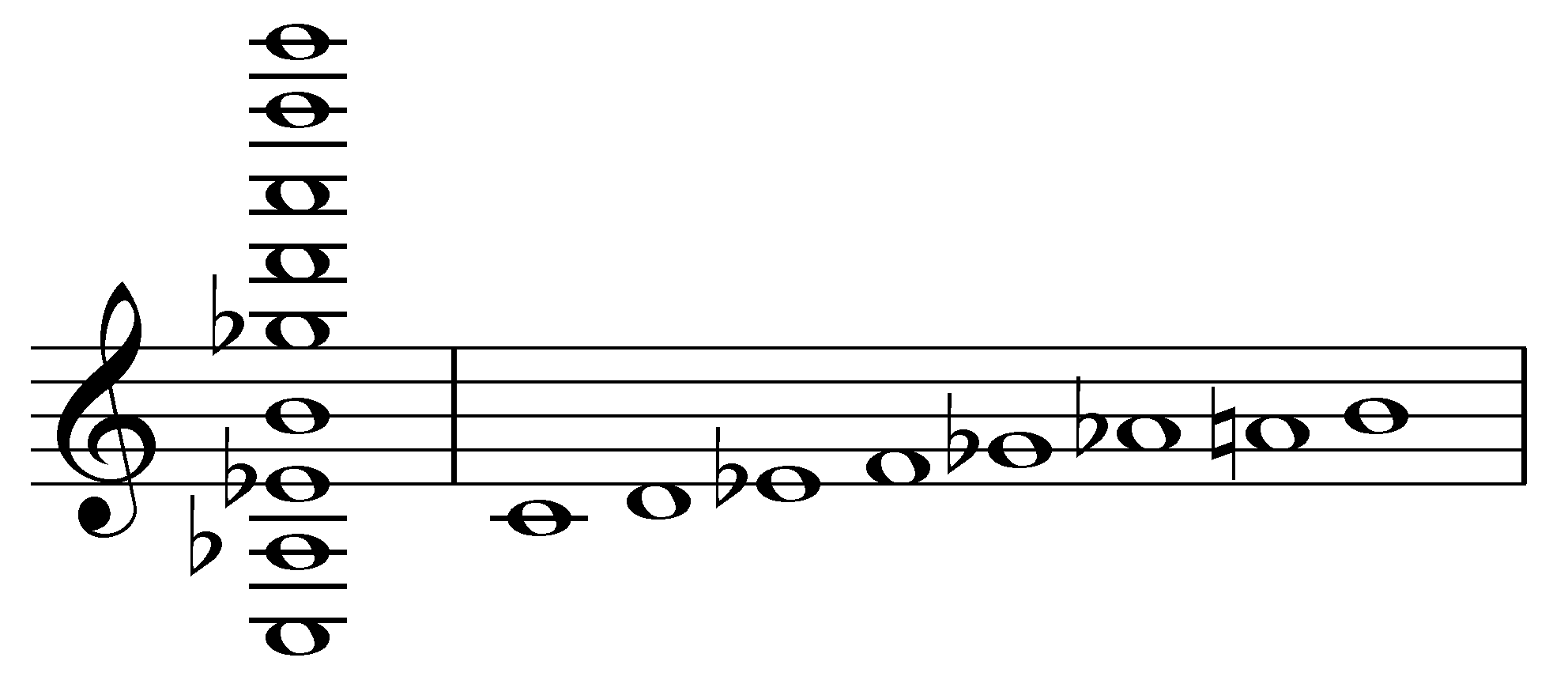
diatonic set theory Diatonic set theory is a subdivision or application of set theory (music), musical set theory which applies the techniques and musical analysis, analysis of discrete mathematics to properties of the diatonic collection such as maximal evenness, Myh ...

, a bisector divides the

octave In music, an octave (: eighth) or perfect octave (sometimes called the diapason) is an interval between two notes, one having twice the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referr ...

approximately in half (the equal tempered

tritone In music theory, the tritone is defined as a interval (music), musical interval spanning three adjacent Major second, whole tones (six semitones). For instance, the interval from F up to the B above it (in short, F–B) is a tritone as it can be ...

is exactly half the octave) and may be used in place of a generator to derive collections for which structure implies multiplicity is not true such as the ascending melodic minor, harmonic minor, and

octatonic scale An octatonic scale is any eight-note musical scale. However, the term most often refers to the ancohemitonic symmetric scale composed of alternating whole and half steps, as shown at right. In classical theory (in contrast to jazz theory), ...

s. Well formed generated collections generators and bisectors coincide, such as the

perfect fifth In music theory, a perfect fifth is the Interval (music), musical interval corresponding to a pair of pitch (music), pitches with a frequency ratio of 3:2, or very nearly so. In classical music from Western culture, a fifth is the interval f ...

(

circle of fifths In music theory, the circle of fifths (sometimes also cycle of fifths) is a way of organizing pitches as a sequence of perfect fifths. Starting on a C, and using the standard system of tuning for Western music (12-tone equal temperament), the se ...

) in the diatonic collection. The term was introduced by Jay Rahn (1977), who considers any division between one and two thirds as approximately half (

major third In music theory, a third is a Interval (music), musical interval encompassing three staff positions (see Interval (music)#Number, Interval number for more details), and the major third () is a third spanning four Semitone, half steps or two ...

minor sixth In music theory, a minor sixth is a musical interval encompassing six staff positions (see Interval number for more details), and is one of two commonly occurring sixths (the other one being the major sixth). It is qualified as ''minor'' bec ...

or 400 to 800 cents) and who applied the term only the equally spaced collections. Clough and Johnson both adapt the term to apply to generic scale steps. Rahn also uses ''aliquant bisector'' for bisectors which may be used to generate every note in a collection, in which case the bisector and the number of notes must be

coprime In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equiv ...

. Bisectors may be used to produce the

diatonic Diatonic and chromatic are terms in music theory that are used to characterize scales. The terms are also applied to musical instruments, intervals, chords, notes, musical styles, and kinds of harmony. They are very often used as a pair ...

, harmonic minor, and ascending melodic minor collections. (Johnson 2003, p. 97, 101, 158n10-12) The diatonic scale may be derived from a chain of perfect fifths: P5 P5 P5 P5 P5 P5 F C G D A E B = C D E F G A B C. 5, 0, 7, 2, 9, 4, e = 0, 2, 4, 5, 7, 9, e, 0. +7 +7 +7 +7 +7 +7 (mod 12) For example, the octatonic scale may be derived similarly to derivations of the diatonic scale by a chain of perfect fifths (a generator), by using a bisector of 5 scale steps (3 may also be used). However, five steps in the octatonic scale alternates between 7 and 8 semitones, so it is a bisector and not a generator: A5 P5 A5 P5 A5 P5 A5 P5 C A♭ E♭ B G♭ D A F C = C D E♭ F G♭ A♭ A B C. 0, 8, 3, e, 6, 2, 9, 5, 0 = 0, 2, 3, 5, 6, 8, 9, e, 0. 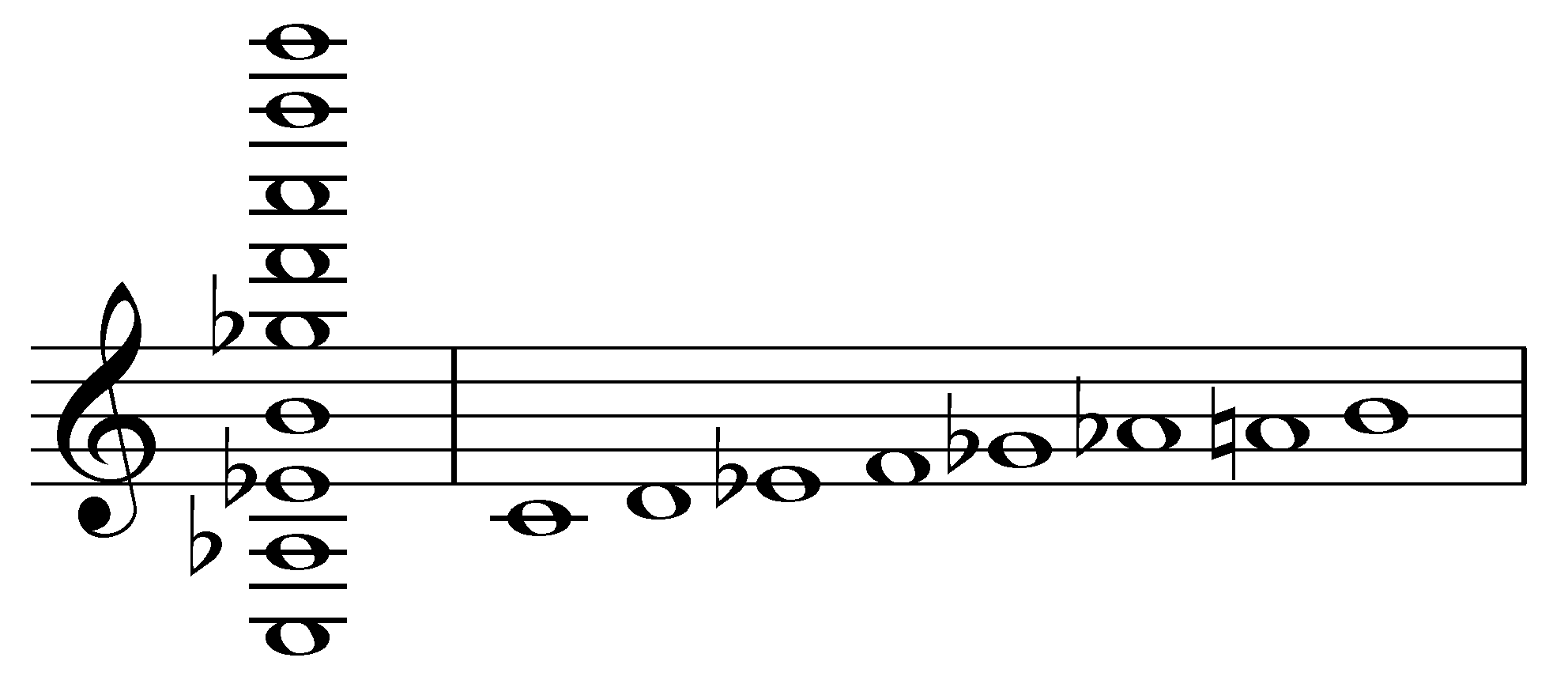+8 +7 +8 +7 +8 +7 +8 +7 Octatonic scale bisector

References

*Johnson, Timothy (2003). ''Foundations of Diatonic Theory: A Mathematically Based Approach to Music Fundamentals''. Key College Publishing. . *Rahn, Jay (1977). "Some Recurrent Features of Scales", ''In Theory Only'' 2, no. 11-12: 43-52 Diatonic set theory Musicology {{music-theory-stub