Antiresonance on:
[Wikipedia]
[Google]
[Amazon]
In the
 The simplest system in which antiresonance arises is a system of coupled harmonic oscillators, for example pendula or
The simplest system in which antiresonance arises is a system of coupled harmonic oscillators, for example pendula or
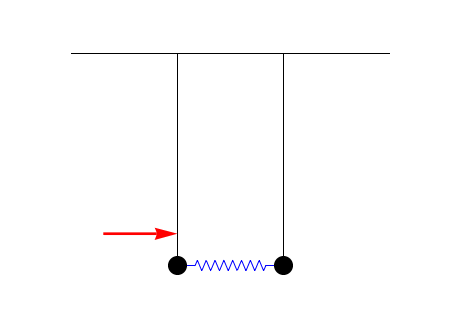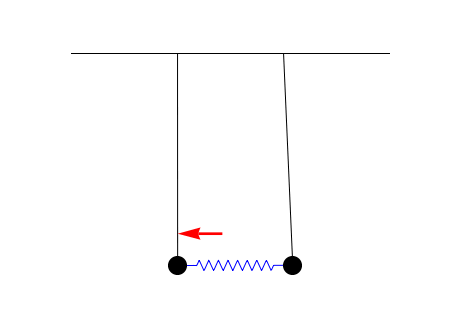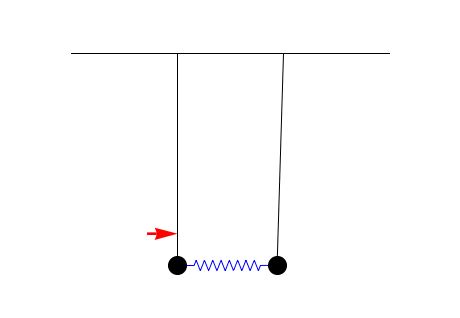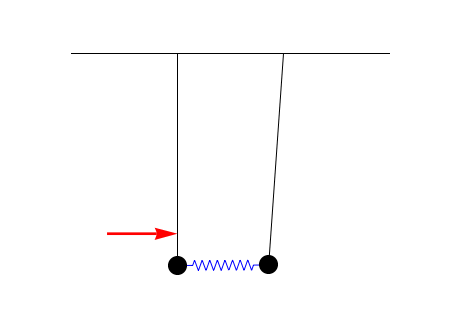 The reduced oscillation amplitude at an antiresonance can be regarded as due to destructive
The reduced oscillation amplitude at an antiresonance can be regarded as due to destructive
 The
The
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
of coupled oscillators, antiresonance, by analogy with resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
, is a pronounced minimum in the amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
of an oscillator
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
at a particular frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
, accompanied by a large, abrupt shift in its oscillation phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
*Phase space, a mathematica ...
. Such frequencies are known as the system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
's antiresonant frequencies, and at these frequencies the oscillation amplitude can drop to almost zero. Antiresonances are caused by destructive interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extra ...
, for example between an external driving force and interaction with another oscillator.
Antiresonances can occur in all types of coupled oscillator systems, including mechanical
Mechanical may refer to:
Machine
* Machine (mechanical), a system of mechanisms that shape the actuator input to achieve a specific application of output forces and movement
* Mechanical calculator, a device used to perform the basic operations o ...
, acoustical, electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interacti ...
, and quantum
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This me ...
systems. They have important applications in the characterization of complicated coupled systems.
The term ''antiresonance'' is used in electrical engineering for a form of resonance in a single oscillator with similar effects.
Antiresonance in electrical engineering
Inelectrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, antiresonance is the condition for which the reactance vanishes but the resistive impedance of an electrical circuit
An electrical network is an interconnection of electrical components (e.g., battery (electricity), batteries, resistors, inductors, capacitors, switches, transistors) or a model of such an interconnection, consisting of electrical elements (e. ...
is none the less very high, approaching infinity.
In an electric circuit consisting of a capacitor and an inductor in parallel, antiresonance occurs when the alternating current
Alternating current (AC) is an electric current that periodically reverses direction and changes its magnitude continuously with time, in contrast to direct current (DC), which flows only in one direction. Alternating current is the form in w ...
line voltage
Voltage, also known as (electrical) potential difference, electric pressure, or electric tension, is the difference in electric potential between two points. In a Electrostatics, static electric field, it corresponds to the Work (electrical), ...
and the resultant current are in phase
Phase or phases may refer to:
Science
*State of matter, or phase, one of the distinct forms in which matter can exist
*Phase (matter), a region of space throughout which all physical properties are essentially uniform
*Phase space, a mathematica ...
. Under these conditions the line current is very small because of the high electrical impedance
In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of Electrical_resistance, resistance and Electrical_reactance, reactance in a electrical circuit, circuit.
Quantitatively, the impedan ...
of the parallel circuit at antiresonance. The branch currents are almost equal in magnitude and opposite in phase.
Antiresonance in coupled oscillators
RLC circuit
An RLC circuit is an electrical circuit consisting of a electrical resistance, resistor (R), an inductor (L), and a capacitor (C), connected in series or in parallel. The name of the circuit is derived from the letters that are used to denote ...
s.
Consider two harmonic oscillators coupled together with strength and with one oscillator driven by an oscillating external force . The situation is described by the coupled ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable (mathematics), variable. As with any other DE, its unknown(s) consists of one (or more) Function (mathematic ...
s
:
where the represent the resonance frequencies of the two oscillators and the their damping rates. Changing variables to the complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
parameters:
:
allows us to write these as first-order equations:
:
We transform to a frame rotating at the driving frequency
:
yielding
:
where we have introduced the detunings between the drive and the oscillators' resonance frequencies. Finally, we make a rotating wave approximation, neglecting the fast counter-rotating terms proportional to , which average to zero over the timescales we are interested in (this approximation assumes that , which is reasonable for small frequency ranges around the resonances). Thus we obtain:
:
Without damping, driving or coupling, the solutions to these equations are:
:
which represent a rotation in the complex plane with angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
.
The steady-state
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' ...
solution can be found by setting , which gives:
:
Examining these steady state solutions as a function of driving frequency, it is evident that both oscillators display resonances (peaks in amplitude accompanied by positive phase shifts) at the two normal mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies ...
frequencies. In addition, the driven oscillator displays a pronounced dip in amplitude between the normal modes which is accompanied by a negative phase shift. This is the antiresonance. Note that there is no antiresonance in the undriven oscillator's spectrum
A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics to describe the rainbow of co ...
; although its amplitude has a minimum between the normal modes, there is no pronounced dip or negative phase shift.
Interpretation as destructive interference
 The reduced oscillation amplitude at an antiresonance can be regarded as due to destructive
The reduced oscillation amplitude at an antiresonance can be regarded as due to destructive interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extra ...
or cancellation of forces acting on the oscillator.
In the above example, at the antiresonance frequency the external driving force acting on oscillator 1 cancels the force acting via the coupling to oscillator 2, causing oscillator 1 to remain almost stationary.
Complicated coupled systems
frequency response function
In signal processing and electronics, the frequency response of a system is the quantitative measure of the magnitude and phase of the output as a function of input frequency. The frequency response is widely used in the design and analysis of s ...
(FRF) of any linear dynamic system composed of many coupled components will in general display distinctive resonance-antiresonance behavior when driven.
As a rule of thumb, it can be stated that as the distance between the driven component and the measured component increases, the number of antiresonances in the FRF decreases. For example, in the two-oscillator situation above, the FRF of the undriven oscillator displayed no antiresonance. Resonances and antiresonances only alternate continuously in the FRF of the driven component itself.
Applications
An important result in the theory of antiresonances is that they can be interpreted as the resonances of the system fixed at the excitation point. This can be seen in the pendulum animation above: the steady-state antiresonant situation is the same as if the left pendulum were fixed and could not oscillate. An important corollary of this result is that the antiresonances of a system are independent of the properties of the driven oscillator; that is, they do not change if the resonance frequency or damping coefficient of the driven oscillator are altered. This result makes antiresonances useful in characterizing complex coupled systems which cannot be easily separated into their constituent components. The resonance frequencies of the system depend on the properties of all components and their couplings, and are independent of which is driven. The antiresonances, on the other hand, are dependent upon everything except the component being driven, therefore providing information about how it affects the total system. By driving each component in turn, information about all of the individual subsystems can be obtained, despite the couplings between them. This technique has applications inmechanical engineering
Mechanical engineering is the study of physical machines and mechanism (engineering), mechanisms that may involve force and movement. It is an engineering branch that combines engineering physics and engineering mathematics, mathematics principl ...
, structural analysis
Structural analysis is a branch of solid mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on physical structures and their c ...
, and the design of integrated quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation, similar to classical circuits, in which a computation is a sequence of quantum gates, measurements, initializations of qubits to known values, and possibly o ...
s.
In electrical engineering antiresonance is used in wave traps, which are sometimes inserted in series with antennas of radio receiver
In radio communications, a radio receiver, also known as a receiver, a wireless, or simply a radio, is an electronic device that receives radio waves and converts the information carried by them to a usable form. It is used with an antenna. ...
s to block the flow of alternating current at the frequency of an interfering station, while allowing other frequencies to pass.
In nanomechanical systems, the sideband spectra of a driven nonlinear mode with its eigenfrequency being modulated at a low frequency (<1 kHz) shows prominent antiresonance line shapes in the power spectra, which can be controlled through the vibration state. The antiresonance frequency can be utilized to characterize the thermal fluctuation and the squeezing parameter of the nonlinear system.
See also
*Resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
* Oscillator
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
* Resonance (alternating-current circuits)
* Tuned mass damper
* Fano resonance
References
{{reflist, 25em Oscillation