Alhazen's problem on:
[Wikipedia]
[Google]
[Amazon]
 Alhazen's problem is a
Alhazen's problem is a
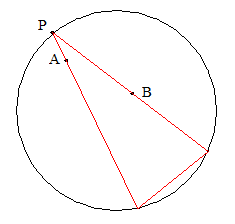 The same problem can be formulated with the two given points inside the circle instead of outside. In this case the solution describes the path of a
The same problem can be formulated with the two given points inside the circle instead of outside. In this case the solution describes the path of a  Another way of describing the problem, for points inside or outside the circle, is that it seeks an
Another way of describing the problem, for points inside or outside the circle, is that it seeks an
 By the time of
By the time of  The number of solutions, for points inside the circle, can also be determined geometrically. In general terms, pairs of given points that are near each other within the circle, and near to the center of the circle, have two reflection points; pairs of points that are far apart and far from the center have four reflections. If one given point is fixed, the positions of the other point that produce two reflections are separated from the positions that produce four reflections by the
The number of solutions, for points inside the circle, can also be determined geometrically. In general terms, pairs of given points that are near each other within the circle, and near to the center of the circle, have two reflection points; pairs of points that are far apart and far from the center have four reflections. If one given point is fixed, the positions of the other point that produce two reflections are separated from the positions that produce four reflections by the
 According to
According to

345
} {{citation , last = Smith , first = A. Mark , date = September 2008 , doi = 10.1017/s0957423908000520 , issue = 2 , journal = Arabic Sciences and Philosophy , pages = 143–163 , title = Alhacen's approach to 'Alhazen's problem' , volume = 18 {{Citation , last1=Agrawal , first1=Amit , last2=Taguchi , first2=Yuichi , last3=Ramalingam , first3=Srikumar , year=2011 , contribution=Beyond Alhazen's problem: Analytical projection model for non-central catadioptric cameras with quadric mirrors , title=IEEE Conference on Computer Vision and Pattern Recognition, doi=10.1109/CVPR.2011.5995596 , title-link=Conference on Computer Vision and Pattern Recognition, pages=2993–3000 , isbn=978-1-4577-0394-2 , contribution-url=http://www.umiacs.umd.edu/~aagrawal/cvpr11/fp/fp.html , url-status=dead , archive-url=https://web.archive.org/web/20120307040949/http://www.umiacs.umd.edu/~aagrawal/cvpr11/fp/fp.html , archive-date=2012-03-07 {{citation , last1=Baker , first1=Marcus, author1-link=Marcus Baker , title=Alhazen's problem: Its bibliography and an extension of the problem , journal=
mathematical problem
A mathematical problem is a problem that can be represented, analyzed, and possibly solved, with the methods of mathematics. This can be a real-world problem, such as computing the orbits of the planets in the Solar System, or a problem of a more ...
in optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
concerning reflection in a spherical mirror. It asks for the point in the mirror where one given point reflects to another.
The special case of a concave spherical mirror is also known as Alhazen's billiard problem, as it can be formulated equivalently as constructing a reflected path from one billiard ball to another on a circular billiard table. Other equivalent formulations ask for the shortest path from one point to the other that touches the circle, or for an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
that is tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
to the circle and has the given points as its foci.
Although special cases of this problem were studied by Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
, it is named for the 11th-century Arab mathematician Alhazen
Ḥasan Ibn al-Haytham ( Latinized as Alhazen; ; full name ; ) was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the princ ...
(''Ibn al-Haytham''), who formulated it more generally and presented a solution in his ''Book of Optics
The ''Book of Optics'' (; or ''Perspectiva''; ) is a seven-volume treatise on optics and other fields of study composed by the medieval Arab scholar Ibn al-Haytham, known in the West as Alhazen or Alhacen (965–c. 1040 AD).
The ''Book ...
''. It has no straightedge and compass construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
; instead, al-Haytham and others including Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
found solutions involving the intersection of conic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
s. According to Roberto Marcolongo
Roberto Marcolongo (August 28, 1862 in Rome – May 16, 1943 in Rome) was an Italian mathematician, known for his research in vector calculus and theoretical physics.
Biography
Marcolongo graduated in 1886, and later he was an assistant of Valent ...
, Leonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested o ...
invented a mechanical device to solve the problem. Later mathematicians, starting with in 1965, solved the problem algebraically as the solution to a quartic equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is
:ax^4+bx^3+cx^2+dx+e=0 \,
where ''a'' ≠ 0.
The quartic is the highest order polynom ...
, and used this equation to prove the impossibility of solving the problem with straightedge and compass.
Researchers have extended this problem and the methods used to solve it to mirrors of other shapes and to non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean ge ...
.
Formulation
The problem comprises drawing lines from two points, meeting at a third point on thecircumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
(boundary) of a circle and making equal angles with the normal at that point (specular reflection
Specular reflection, or regular reflection, is the mirror-like reflection (physics), reflection of waves, such as light, from a surface.
The law of reflection states that a reflected ray (optics), ray of light emerges from the reflecting surf ...
). It belongs to geometrical optics
Geometrical optics, or ray optics, is a model of optics that describes light Wave propagation, propagation in terms of ''ray (optics), rays''. The ray in geometrical optics is an abstract object, abstraction useful for approximating the paths along ...
(in which light is modeled using rays rather than waves or particles), and catoptrics, the use of mirrors to control light: it can be used to find the path of a ray of light that starts at one point of space, is reflected from a spherical mirror, and passes through a second point. Although this is a three-dimensional problem, it can immediately be reduced to the two-dimensional problem of reflection in a circular mirror in the plane, because its solution lies entirely within the plane formed by the two points and the center of the sphere.
 The same problem can be formulated with the two given points inside the circle instead of outside. In this case the solution describes the path of a
The same problem can be formulated with the two given points inside the circle instead of outside. In this case the solution describes the path of a billiards
Cue sports are a wide variety of games of skill played with a cue stick, which is used to strike billiard balls and thereby cause them to move around a cloth-covered table bounded by elastic bumpers known as . Cue sports, a category of stic ...
ball reflected within a circular billiards table, as Lewis Carroll
Charles Lutwidge Dodgson (27 January 1832 – 14 January 1898), better known by his pen name Lewis Carroll, was an English author, poet, mathematician, photographer and reluctant Anglicanism, Anglican deacon. His most notable works are ''Alice ...
once suggested for billiards play. Because the two chords of the circle through the given points and the reflection point form equal angles with the circle, they form the two equal sides of an isosceles triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at le ...
inscribed within the circle, with the two given points on these two sides. Another equivalent form of Alhazen's problem asks to construct this triangle. For points near each other within the solution, in general position
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the ''general case'' situation, as opposed to some more special or coincidental cases that a ...
, there will be two solutions, but points that are farther apart have four solutions.
 Another way of describing the problem, for points inside or outside the circle, is that it seeks an
Another way of describing the problem, for points inside or outside the circle, is that it seeks an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
having the two given points as its foci, tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points o ...
to the given circle. The point of tangency is the solution point to Alhazen's problem. A ray from one focus of the ellipse to this point of tangency will be reflected by the ellipse to the other focus, and because the given circle has the same angle at the point of tangency, it will also reflect the same ray in the same way. The smallest such ellipse has as its point of tangency the point of the circle whose sum of distances to the two given points is minimum. The equivalence between finding the path of a reflected light ray and minimizing the total length of the path is Hero's principle, later reformulated in Fermat's principle
Fermat's principle, also known as the principle of least time, is the link between geometrical optics, ray optics and physical optics, wave optics. Fermat's principle states that the path taken by a Ray (optics), ray between two given ...
as minimizing the total time traveled by the ray. More generally, as James Gregory observed, for any analogous three-dimensional reflection problem, the point of reflection is also a point of tangency of an ellipsoid
An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional Scaling (geometry), scalings, or more generally, of an affine transformation.
An ellipsoid is a quadric surface; that is, a Surface (mathemat ...
having the source and destination of the reflected ray as its foci.
Ptolemy included the problem of reflection in a circular mirror in his ''Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
'' (written in the second century AD), but was only able to solve certain special cases; al-Haytham formulated and solved the problem more generally. Al-Haytham was inspired by Ptolemy's work, and modeled his own book on Ptolemy's, but differed from it in important ways; for instance, Ptolemy used a model of visual perception in which visual rays travel outward from the eye to the objects it sees, while al-Haytham reversed this to the still-used model in which light rays travel inward from objects to the eye.
Solutions
Geometric
Pappus of Alexandria
Pappus of Alexandria (; ; AD) was a Greek mathematics, Greek mathematician of late antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem in projective geometry. Almost nothing is known a ...
, Greek mathematicians had categorized geometric solutions into three types: straightedge and compass construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
s, constructions using conic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
s, and neusis constructions involving a marked ruler, preferring the earlier categories of solution over the later ones. Ibn al-Haytham's solution is of the second type, using hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component ( ...
, through which he develops a neusis construction. In his 1881 survey of the problem, Marcus Baker
Marcus Baker (September 23, 1849 – December 12, 1903) was an American naturalist, explorer of Alaska, journalist, and newspaper editor.
Early life and education
Baker was born September 23, 1849, in Kalamazoo, Michigan, and graduated fr ...
calls al-Haytham's solution "excessively prolix and intricate", and quotes Isaac Barrow
Isaac Barrow (October 1630 – 4 May 1677) was an English Christian theologian and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for proof of the fundamental theorem ...
as expressing a similar opinion. Later in the 11th century, Yusuf al-Mu'taman ibn Hud, a king of the Taifa of Zaragoza
The taifa of Zaragoza () was an independent Arab Muslim state in the east of Al-Andalus (present-day Spain) with its capital in Saraqusta (Zaragoza) city. It was established in the early 11th century as one of the many Taifa kingdoms that foll ...
in Spain, simplified al-Haytham's lemmas somewhat, but did not make a significant advance on the problem. The work of al-Haytham became known in the rest of Europe through manuscript Latin translations in the 12th or 13th century, and a translation was published in Basel
Basel ( ; ), also known as Basle ( ), ; ; ; . is a city in northwestern Switzerland on the river Rhine (at the transition from the High Rhine, High to the Upper Rhine). Basel is Switzerland's List of cities in Switzerland, third-most-populo ...
in 1572. Later geometric solutions by Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
, René-François de Sluse, and Guillaume de l'Hôpital
Guillaume François Antoine, Marquis de l'Hôpital (; sometimes spelled L'Hospital; 7 June 1661 – 2 February 1704) was a French mathematician. His name is firmly associated with l'Hôpital's rule for calculating limits involving indetermin ...
used the same idea of an auxiliary conic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
: a hyperbola for Huygens, a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
for Sluse, and both methods for l'Hôpital. Baker cites Huygens's solution as "the most elegant the problem has ever received".
In al-Haytham's solution, the hyperbola is used within a construction of the angle of reflection, after which the point of reflection is easy to find. Al-Haytham further subdivides the problem into cases, according to the number of reflected images (one for a convex mirror but up to four for a concave mirror), and solves each case separately. Instead, Huygens finds a hyperbola that directly solves the problem in all cases: the reflection points are points of intersection between this hyperbola and the given circle. This hyperbola can be characterized in many ways; one way involves inversive geometry
In geometry, inversive geometry is the study of ''inversion'', a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry ...
. Inverting a point through a circle produces another point, on the same ray from the center of the circle, such that the product of distances of the point and its inverse from the center equals the squared radius of the circle. The locus of points at which the two lines to the given points cross, at equal angles, a circle concentric to the given one, is a cubic curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation
:
applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an eq ...
containing both given points. The inversion of through the given circle is a rectangular hyperbola
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirro ...
, passing through the two points inverse to the given points and centered at the midpoint of the two inverse points. Its asymptotic lines are parallel to and perpendicular to the angle bisector of the angle subtended by the given points (or their inverses) at the center of the circle. The intersections of this hyperbola with the given circle include the desired solution point or points.
Certain special cases admit simpler solutions. For two given points equidistant from the center of the circle, the reflection point or points occur where the circle is crossed by the perpendicular bisector of the two points. And for two given points that lie on a single diameter of the circle, there are one or two reflection points where this diameter crosses the circle. As well, when the two points on the diameter are interior to the circle, there may be two more reflection points, where the given circle is crossed by an Apollonian circle through the center of the circle. This circle is the locus of points whose ratio of distances to the two given points is constant. If the Apollonian circle crosses the given circle, reflection points occur at the crossings; however, it may remain entirely within the given circle, in which case the only reflection points are the endpoints of the diameter.
 The number of solutions, for points inside the circle, can also be determined geometrically. In general terms, pairs of given points that are near each other within the circle, and near to the center of the circle, have two reflection points; pairs of points that are far apart and far from the center have four reflections. If one given point is fixed, the positions of the other point that produce two reflections are separated from the positions that produce four reflections by the
The number of solutions, for points inside the circle, can also be determined geometrically. In general terms, pairs of given points that are near each other within the circle, and near to the center of the circle, have two reflection points; pairs of points that are far apart and far from the center have four reflections. If one given point is fixed, the positions of the other point that produce two reflections are separated from the positions that produce four reflections by the caustic
Caustic most commonly refers to:
* Causticity, the property of being able to corrode organic tissue
** Sodium hydroxide, sometimes called ''caustic soda''
** Potassium hydroxide, sometimes called ''caustic potash''
** Calcium oxide, sometimes cal ...
generated by the reflections of a light source at the fixed point. On the caustic itself, away from its cusps, there are three reflections. At the cusps there are only two reflections.
The impossibility of a straightedge and compass solution was finally proven in 1965, using algebraic methods, by Jack M. Elkin (an actuary
An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require investment management, asset management, ...
). A similar impossibility proof was rediscovered in 1997 by Oxford
Oxford () is a City status in the United Kingdom, cathedral city and non-metropolitan district in Oxfordshire, England, of which it is the county town.
The city is home to the University of Oxford, the List of oldest universities in continuou ...
mathematician Peter M. Neumann. The neusis construction can also be carried out using origami
) is the Japanese art of paper folding. In modern usage, the word "origami" is often used as an inclusive term for all folding practices, regardless of their culture of origin. The goal is to transform a flat square sheet of paper into a ...
folds following the Huzita–Hatori axioms, and Roger C. Alperin has argued through algebraic methods that the problem can be solved by straightedge, compass, and angle trisector, but without providing an explicit construction.
Mechanical
Roberto Marcolongo
Roberto Marcolongo (August 28, 1862 in Rome – May 16, 1943 in Rome) was an Italian mathematician, known for his research in vector calculus and theoretical physics.
Biography
Marcolongo graduated in 1886, and later he was an assistant of Valent ...
, a mechanical solution was presented by Leonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested o ...
, after failing to find a mathematical solution. The solution, as reconstructed by Marcolongo, takes the form of a mechanical linkage that, when placed with its tip pinned to the circle center and the two given points allowed to slide along its arms, always maintains equal angles to these points at the hinge point of the two arms. Therefore, if the mechanism is moved in order to place this hinge point on the given circle, the solution will be obtained at this point.
Algebraic
Later mathematicians such as James Gregory and many others attempted to find an algebraic solution to the problem, using various methods, including analytic methods of geometry and derivation bycomplex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s. An algebraic solution to the problem was finally found in 1965 by Elkin, by means of a quartic polynomial
In algebra, a quartic function is a function of the form
:f(x)=ax^4+bx^3+cx^2+dx+e,
where ''a'' is nonzero,
which is defined by a polynomial of degree four, called a quartic polynomial.
A ''quartic equation'', or equation of the fourth de ...
.
Other solutions were rediscovered later: in 1989, by Harald Riede; in 1990 (submitted in 1988), by Miller and Vegh;
and in 1992, by John D. Smith
and also by Jörg Waldvogel.
Waldvogel simplifies the algebra by formulating the problem for the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
and two given points and in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
. With the aid of Huygens's hyperbola Waldvogel derives a quartic equation for the reflection point , where and are the complex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
s of and . The roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusin ...
of this equation might not all lie on the unit circle; the desired solution is the root that does lie on the circle and minimizes the sum of distances to the given points. With some further manipulation this can be reformulated as an equation involving real numbers instead of complex numbers.
The algebraic solution of this problem allows the use of Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
to prove that, for certain easily constructed inputs, the solution point has coordinates that are not constructible numbers, and therefore that the problem has no straightedge and compass solution. For example, a construction of shows that the two given points and have reflection points on the unit circle whose coordinates come from roots of the polynomial , which has the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric grou ...
on four elements as its Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the pol ...
. It follows that the reflection point cannot be constructed with straightedge and compass. Carréga and Haddad generalize this example to pairs of rational points whose reflection points give the roots of any ''Stewart polynomial'' and show that this leads to unconstructible points whenever is a prime number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...
.
Trigonometric and numeric
Isaac Barrow
Isaac Barrow (October 1630 – 4 May 1677) was an English Christian theologian and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for proof of the fundamental theorem ...
, in a set of lectures in 1669,
used a trigonometric equation in polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
to describe the cubic curve
In mathematics, a cubic plane curve is a plane algebraic curve defined by a cubic equation
:
applied to homogeneous coordinates for the projective plane; or the inhomogeneous version for the affine space determined by setting in such an eq ...
inverse to Huygens's hyperbola. It has the same property as the hyperbola: it intersects the given circle at the reflection point or points that solve the problem.
derive a messy equation involving square roots of polynomials of trigonometric function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
s for the angle around the circle of the reflection point. They suggest the use of Newton's method
In numerical analysis, the Newton–Raphson method, also known simply as Newton's method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a ...
to solve this equation numerically, but this involves the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of one side of the equation, and they write that finding this derivative explicitly is "certainly not the way to go". Instead, for this part they use automatic differentiation
In mathematics and computer algebra, automatic differentiation (auto-differentiation, autodiff, or AD), also called algorithmic differentiation, computational differentiation, and differentiation arithmetic Hend Dawood and Nefertiti Megahed (2023) ...
.
For inputs at which the segment from one given point to the reflection point is perpendicular to the segment between the other given point and the circle center, the Huygens hyperbola degenerates to two lines. This degeneracy can lead certain numerical solutions of Alhazen's problem to become unstable near these inputs. Additional forms of instability can arise when the circle radius is much smaller than its distance to the two given points. To avoid these issues, reformulate the problem as a trigonometric equation with, in general, 16 solutions, but for which it is possible to predetermine which of these solutions is the desired one. This leads to an iterative numerical solution that is fast and robust, which they apply in planetary science
Planetary science (or more rarely, planetology) is the scientific study of planets (including Earth), celestial bodies (such as moons, asteroids, comets) and planetary systems (in particular those of the Solar System) and the processes of ...
.
Generalization
As well as spherical mirrors, al-Haytham also studied conical and cylindrical mirrors, which can be reduced in the same way as a spherical mirror to reflection in a circular mirror in the plane. Researchers have extended Alhazen's problem to general rotationally symmetricquadric
In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids.
More generally, a quadric hype ...
mirrors, including hyperbolic, parabolic and elliptical mirrors. They showed that the mirror reflection point can be computed by solving an eighth-degree equation in the most general case. If the camera (eye) is placed on the axis of the mirror, the degree of the equation reduces to six. Alhazen's problem can also be extended to multiple refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
s from a spherical ball. Given a light source and a spherical ball of certain refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
, the closest point on the spherical ball where the light is refracted to the eye of the observer can be obtained by solving a tenth-degree equation.
Another direction for generalization is to non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean ge ...
. In the hyperbolic plane, as in the Euclidean plane, it is not possible to solve the problem using only a straightedge and compass.
References
{{reflist, refs= {{citation , last = Hogendijk , first = Jan P. , author-link = Jan Hogendijk , contribution = Al-Muʾtaman's simplified lemmas for solving 'Alhazen's problem' , mr = 1459724 , pages = 59–101 , publisher = Univ. Barcelona, Barcelona , series = Anu. Filol. Univ. Barc. , title = From Baghdad to Barcelona/De Bagdad a Barcelona, Vol. I, II (Zaragoza, 1993) , volume = XIX B-2 , year = 1996 {{Citation , last1=Agrawal , first1=Amit , last2=Taguchi , first2=Yuichi , last3=Ramalingam , first3=Srikumar , year=2010 , title=Analytical forward projection for axial non-central dioptric and catadioptric cameras , publisher=European Conference on Computer Vision , url=http://www.umiacs.umd.edu/~aagrawal/eccv10/fp/fp.html , url-status=dead , archive-url=https://web.archive.org/web/20120307042704/http://www.umiacs.umd.edu/~aagrawal/eccv10/fp/fp.html , archive-date=2012-03-07 {{citation, title=The Ancient Tradition of Geometric Problems, title-link=The Ancient Tradition of Geometric Problems, series=Dover Books on Mathematics, first=Wilbur Richard, last=Knorr, author-link=Wilbur Knorr, publisher=Courier Corporation, year=1993, isbn=9780486675329, pag345
} {{citation , last = Smith , first = A. Mark , date = September 2008 , doi = 10.1017/s0957423908000520 , issue = 2 , journal = Arabic Sciences and Philosophy , pages = 143–163 , title = Alhacen's approach to 'Alhazen's problem' , volume = 18 {{Citation , last1=Agrawal , first1=Amit , last2=Taguchi , first2=Yuichi , last3=Ramalingam , first3=Srikumar , year=2011 , contribution=Beyond Alhazen's problem: Analytical projection model for non-central catadioptric cameras with quadric mirrors , title=IEEE Conference on Computer Vision and Pattern Recognition, doi=10.1109/CVPR.2011.5995596 , title-link=Conference on Computer Vision and Pattern Recognition, pages=2993–3000 , isbn=978-1-4577-0394-2 , contribution-url=http://www.umiacs.umd.edu/~aagrawal/cvpr11/fp/fp.html , url-status=dead , archive-url=https://web.archive.org/web/20120307040949/http://www.umiacs.umd.edu/~aagrawal/cvpr11/fp/fp.html , archive-date=2012-03-07 {{citation , last1=Baker , first1=Marcus, author1-link=Marcus Baker , title=Alhazen's problem: Its bibliography and an extension of the problem , journal=
American Journal of Mathematics
The ''American Journal of Mathematics'' is a bimonthly mathematics journal published by the Johns Hopkins University Press.
History
The ''American Journal of Mathematics'' is the oldest continuously published mathematical journal in the United S ...
, volume=4 , issue=1/4 , year=1881 , pages=327–331 , doi=10.2307/2369168 , jstor=2369168
{{citation
, last1 = Drexler , first1 = Michael
, last2 = Gander , first2 = Martin J.
, bibcode = 1998SIAMR..40..315D
, doi = 10.1137/S0036144596310872
, issue = 2
, journal = SIAM Review
Society for Industrial and Applied Mathematics (SIAM) is a professional society dedicated to applied mathematics, computational science, and data science through research, publications, and community. SIAM is the world's largest scientific socie ...
, pages = 315–323
, title = Circular billiard
, url = https://archive-ouverte.unige.ch/unige:6305
, volume = 40
, year = 1998
{{citation
, last = Bruins , first = Evert M.
, date = September 1969
, doi = 10.1111/j.1600-0498.1969.tb00124.x
, issue = 3
, journal = Centaurus
, pages = 269–277
, title = Problema Alhaseni at the tercentenary of Huygens' solution
, volume = 13, bibcode = 1969Cent...13..269B
{{citation
, last1 = Peña Queralt , first1 = Laura
, last2 = Blanco Abellán , first2 = Mónica
, last3 = Massa Esteve , first3 = Maria Rosa
, hdl = 2117/342686
, journal = Quaderns d'història de l'enginyeria
, language = ca
, pages = 13–47
, title = Mètodes analítics en el s.XVII: l'Hospital i el problema d'Alhazen
, volume = 18
, year = 2020
{{citation
, last = Smith , first = A. Mark
, editor1-first = Trevor H. , editor1-last = Levere
, editor2-first = William R. , editor2-last = Shea
, contribution = Alhazen's Debt to Ptolemy's ''Optics''
, doi = 10.1007/978-94-009-1878-8_6
, isbn = 9789400918788
, pages = 147–164
, publisher = Springer Netherlands
, title = Nature, Experiment, and the Sciences: Essays on Galileo and the History of Science in Honour of Stillman Drake
, series = Boston Studies in the Philosophy of Science
, year = 1990, volume = 120
{{Citation , last=Highfield , first=Roger , date=1 April 1997 , title=Don solves the last puzzle left by ancient Greeks , journal=Electronic Telegraph
''The Daily Telegraph'', known online and elsewhere as ''The Telegraph'', is a British daily broadsheet conservative newspaper published in London by Telegraph Media Group and distributed in the United Kingdom and internationally. It was found ...
, volume=676 , url=https://www.telegraph.co.uk/htmlContent.jhtml?html=/archive/1997/04/01/ngre01.html , access-date=2008-09-24 , url-status=dead , archive-url=https://web.archive.org/web/20041123051228/http://www.telegraph.co.uk/htmlContent.jhtml?html=%2Farchive%2F1997%2F04%2F01%2Fngre01.html , archive-date=November 23, 2004
{{citation
, last = Dörrie , first = Heinrich
, translator-last = Antin , translator-first = David
, contribution = Alhazen's billiard problem
, isbn = 978-0-486-61348-2
, pages = 197–200
, publisher = Dover
, title = 100 Great Problems of Elementary Mathematics
, year = 1965
{{citation
, last = Elkin , first = Jack M.
, doi = 10.5951/MT.58.3.0194
, issue = 3
, journal = The Mathematics Teacher
Founded in 1920, The National Council of Teachers of Mathematics (NCTM) is a professional organization for schoolteachers of mathematics in the United States. One of its goals is to improve the standards of mathematics in education. NCTM holds an ...
, jstor = 27968003
, pages = 194–199
, title = A deceptively easy problem
, volume = 58
, year = 1965
{{citation
, last1 = Huygens , first1 = Christiaan , author1-link = Christiaan Huygens
, last2 = de Sluse , first2 = René-François , author2-link = René-François de Sluse
, date = October 1673
, doi = 10.1098/rstl.1673.0045
, issue = 97
, journal = Philosophical Transactions of the Royal Society of London
''Philosophical Transactions of the Royal Society'' is a scientific journal published by the Royal Society. In its earliest days, it was a private venture of the Royal Society's secretary. It was established in 1665, making it the second journ ...
, language = la
, pages = 6119–6126
, publisher = The Royal Society
, title = Excerpta ex epistolis non-nullis, ultrò citróque ab illustrissimis viris, Slusio & Hugenio, ad editorem scriptis, de famigerato Alhazeni problemate circa punctum reflexionis in speculis cavis aut convexis; & primò quidem ex prima Hugenii, 26 Junii 1669
, volume = 8
{{citation
, last1 = Huygens , first1 = Christiaan , author1-link = Christiaan Huygens
, last2 = de Sluse , first2 = René-François , author2-link = René-François de Sluse
, date = November 1673
, doi = 10.1098/rstl.1673.0049
, issue = 98
, journal = Philosophical Transactions of the Royal Society of London
''Philosophical Transactions of the Royal Society'' is a scientific journal published by the Royal Society. In its earliest days, it was a private venture of the Royal Society's secretary. It was established in 1665, making it the second journ ...
, language = la
, pages = 6140–6146
, publisher = The Royal Society
, title = Continuatio excerptorum ex epistolis Slusianis & Hugenianis, super Alhazeni problemate optico, in act is philosophicis proximè pragressis commemorato. DN. Hugenius ad novissimam Dn.Slusii, p.6123. & seqq. Num. 97. editaru, rescripsit editori, Lutetiâ Parisiorum Apr. 9. 1672
, volume = 8
{{citation
, last1 = Gander , first1 = Walter
, last2 = Gruntz , first2 = Dominik
, date = November 1992
, doi = 10.1080/0020739920230602
, issue = 6
, journal = International Journal of Mathematical Education in Science and Technology
, pages = 825–830
, title = The billiard problem
, volume = 23
{{citation
, last = Glaeser , first = Georg , author-link = Georg Glaeser
, issue = 2
, journal = Journal for Geometry and Graphics
, mr = 1748025
, pages = 121–139
, title = Reflections on spheres and cylinders of revolution
, url = https://sodwana.uni-ak.ac.at/dld/reflections.pdf
, volume = 3
, year = 1999
{{citation , last1=Miller , first1=Allen R. , last2=Vegh , first2=Emanuel , title=Computing the grazing angle of specular reflection , journal=International Journal of Mathematical Education in Science and Technology , volume=21 , issue=2 , year=1990 , pages=271–274 , doi=10.1080/0020739900210213
{{citation
, last1 = Poirier , first1 = Nathan
, last2 = McDaniel , first2 = Michael
, doi = 10.2140/involve.2012.5.273
, issue = 3
, journal = Involve
, mr = 3044613
, pages = 273–282
, title = Alhazen's hyperbolic billiard problem
, volume = 5
, year = 2012
{{citation , last=Riede , first=Harald , title=Reflexion am Kugelspiegel. Oder: das Problem des Alhazen , journal=Praxis der Mathematik , volume=31 , issue=2 , pages=65–70 , year=1989 , language=de
{{citation
, last = Marcolongo , first = Roberto , author-link = Roberto Marcolongo
, language = it
, location = Napoli
, publisher = Unione tipografica combattenti
, title = Lo strumento inventato da Leonardo da Vinci per la risoluzione del problema di Alhazen
, url = https://books.google.com/books?id=30NLAAAAMAAJ&pg=RA2-PP3
, year = 1929
{{citation
, last = Marcolongo , first = Roberto , author-link = Roberto Marcolongo
, contribution = Leonardo da Vinci nelle storia della matamatica e della meccanica, Il problema d'Alhazen
, language = it
, pages = 287–289
, publisher = International Mathematical Union
, title = Proceedings of the International Congress of Mathematicians
, url = https://www.mathunion.org/fileadmin/ICM/Proceedings/ICM1928.1/ICM1928.1.ocr.pdf
, volume = 1
, year = 1928
{{citation , last= Martin , first= George E. , date= 1998 , title= Geometric Constructions , title-link= Geometric Constructions , publisher= Springer-Verlag, New York , series= Undergraduate Texts in Mathematics , isbn= 0-387-98276-0 , pages=138–139
{{citation
, last1 = Carréga , first1 = Jean-Claude
, last2 = Haddad , first2 = Labib
, arxiv = 1510.05912
, issue = 102
, journal = Quadrature
, language = fr
, mr = 3561659
, pages = 24–30
, title = Miroir circulaire et polynômes de Stewart
, year = 2016
{{citation
, last = Jones , first = Alexander
, date = April 1987
, doi = 10.1111/j.1600-0498.1987.tb00671.x
, hdl = 2451/59839
, issue = 1
, journal = Centaurus
Centaurus () is a bright constellation in the southern sky. One of the 88 modern constellations by area, largest constellations, Centaurus was included among the 48 constellations listed by the 2nd-century astronomer Ptolemy, and it remains one ...
, pages = 1–17
, title = On some borrowed and misunderstood problems in Greek catoptrics
, volume = 30, bibcode = 1987Cent...30....1J
, hdl-access = free
{{citation
, last = Neumann , first = Peter M. , author-link = Peter M. Neumann
, doi = 10.1080/00029890.1998.12004920
, issue = 6
, journal = The American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an exposito ...
, jstor = 2589403
, mr = 1626185
, pages = 523–528
, title = Reflections on reflection in a spherical mirror
, volume = 105
, year = 1998
{{citation
, last = Alperin , first = Roger , author-link = Roger C. Alperin
, editor-last=Hull , editor-first=Thomas , editor-link = Tom Hull (mathematician)
, contribution = Mathematical origami: Another view of Alhazen's optical problem
, contribution-url = https://scholar.archive.org/work/opkovqn6brhd3beqoahd7nofrm
, doi = 10.1201/b15735-11
, isbn = 978-0-429-06490-6
, publisher = A K Peters/CRC Press
, title = Origami3: Proceedings of the Third International Meeting of Origami Science, Mathematics, and Education (3OSME), Asilomar, California, USA, 2001
, year = 2002, pages = 95–106
{{citation
, last = Nishimura , first = Yasuzo
, issue = 2
, journal = International Journal of Geometry
, mr = 3867809
, pages = 37–42
, title = Solving Alhazen's problem by origami
, volume = 7
, year = 2018
{{citation
, last = Park , first = David
, isbn = 9780691221670
, pages = 127–128
, publisher = Princeton University Press
, title = The How and the Why: An Essay on the Origins and Development of Physical Theory
, url = https://books.google.com/books?id=KkT_DwAAQBAJ&pg=PA127
, year = 2020
{{citation
, last = Smith , first = A. Mark
, date = March 1998
, doi = 10.1017/s0957423900002423
, issue = 1
, journal = Arabic Sciences and Philosophy
, pages = 9–44
, title = Ptolemy, Alhazen, and Kepler and the problem of optical images
, volume = 8
{{citation
, last = Smith , first = John D.
, doi = 10.2307/3620392
, issue = 475
, journal = The Mathematical Gazette
''The Mathematical Gazette'' is a triannual peer-reviewed academic journal published by Cambridge University Press on behalf of the Mathematical Association. It covers mathematics education with a focus on the 15–20 years age range.
The journ ...
, jstor = 3620392
, pages = 189–198
, title = The remarkable Ibn al-Haytham
, url = https://scholar.archive.org/work/xwmp6su3qrfvllvaovdqguao24
, volume = 76
, year = 1992
{{citation
, last = Sabra , first = A. I. , author-link = A. I. Sabra
, doi = 10.1007/BF00418752
, issue = 4
, journal = Archive for History of Exact Sciences
''Archive for History of Exact Sciences'' is a peer-reviewed academic journal currently published bimonthly by Springer Science+Business Media, covering the history of mathematics and of astronomy observations and techniques, epistemology of scien ...
, jstor = 41133657
, mr = 678121
, pages = 299–324
, title = ibn al-Haytham's lemmas for solving "Alhazen's problem"
, volume = 26
, year = 1982
{{citation
, last = Severi , first = Francesco , author-link = Francesco Severi
, date = January 1953
, issue = 4
, journal = East and West
, jstor = 29758044
, pages = 233–235
, title = Leonardo and mathematics
, volume = 3
{{citation
, last1 = Chen , first1 = Tieling
, last2 = Ilukor , first2 = Paul
, last3 = Koo , first3 = Reginald
, date = March 2024
, doi = 10.2478/rmm-2024-0006
, issue = 18
, journal = Recreational Mathematics Magazine
, pages = 99–109
, title = The one-cushion escape from snooker in a circular table
, volume = 11, doi-access = free
{{citation
, last1 = Fujimura , first1 = Masayo
, last2 = Hariri , first2 = Parisa
, last3 = Mocanu , first3 = Marcelina
, last4 = Vuorinen , first4 = Matti
, arxiv = 1706.06924
, doi = 10.1007/s40315-018-0257-z
, issue = 1
, journal = Computational Methods and Function Theory
, pages = 135–155
, title = The Ptolemy–Alhazen problem and spherical mirror reflection
, volume = 19
, year = 2018
{{citation
, last1 = Miller , first1 = William J.
, last2 = Barnes , first2 = Jason W.
, last3 = MacKenzie , first3 = Shannon M.
, arxiv = 2012.02170
, bibcode = 2021PSJ.....2...63M
, date = March 2021
, doi = 10.3847/psj/abe4dd
, issue = 2
, journal = The Planetary Science Journal
, page = 63
, publisher = American Astronomical Society
, title = Solving the Alhazen–Ptolemy problem: determining specular points on spherical surfaces for radiative transfer of Titan's seas
, volume = 2, doi-access = free
{{citation, url=https://mathtourist.blogspot.com/2020/05/billiards-in-round.html, work=The Mathematical Tourist, date=March 3, 1997, title=Billiards in the round, first=Ivars, last=Peterson, author-link=Ivars Peterson, access-date=2025-06-05
{{citation
, last = Alperin , first = Roger C. , author-link = Roger C. Alperin
, doi = 10.1080/00029890.2005.11920187
, issue = 3
, journal = The American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an exposito ...
, jstor = 30037438
, mr = 2125383
, pages = 200–211
, title = Trisections and totally real origami
, url = https://scholar.archive.org/work/mrsegehepfb4hgtmobpykadcym
, volume = 112
, year = 2005
{{citation
, last = Waldvogel , first = Jörg
, issue = 3
, journal = Elemente der Mathematik
''Elemente der Mathematik'' is a peer-reviewed scientific journal covering mathematics. It is published by the European Mathematical Society Publishing House on behalf of the Swiss Mathematical Society. It was established in 1946 by Louis Loc ...
, pages = 108–113
, title = The problem of the circular billiard
, url = https://eudml.org/doc/141532
, volume = 47
, year = 1992
Mathematical problems
Mathematics in the medieval Islamic world
Geometrical optics
Ibn al-Haytham
Ptolemy