3-body problem on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 In the ''restricted three-body problem'', a body of negligible mass (the "planetoid") moves under the influence of two massive bodies. Having negligible mass, the force that the planetoid exerts on the two massive bodies may be neglected, and the system can be analysed and can therefore be described in terms of a two-body motion. Usually this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.
The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem.
Mathematically, the problem is stated as follows. Let be the masses of the two massive bodies, with (planar) coordinates and , and let be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to . Then, the motion of the planetoid is given by
:
where . In this form the equations of motion carry an explicit time dependence through the coordinates . However, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.
In the ''restricted three-body problem'', a body of negligible mass (the "planetoid") moves under the influence of two massive bodies. Having negligible mass, the force that the planetoid exerts on the two massive bodies may be neglected, and the system can be analysed and can therefore be described in terms of a two-body motion. Usually this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.
The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem.
Mathematically, the problem is stated as follows. Let be the masses of the two massive bodies, with (planar) coordinates and , and let be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to . Then, the motion of the planetoid is given by
:
where . In this form the equations of motion carry an explicit time dependence through the coordinates . However, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.
 There is no general
There is no general
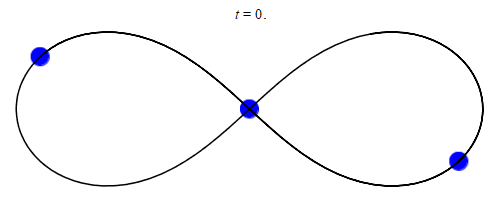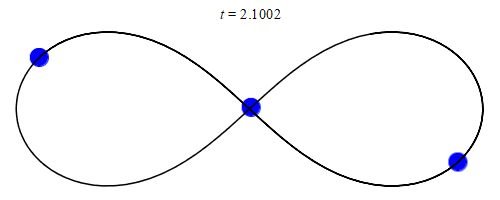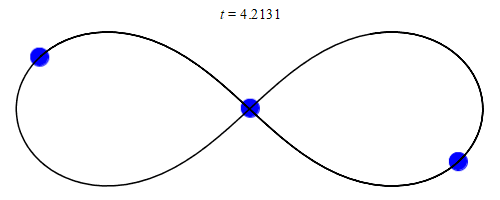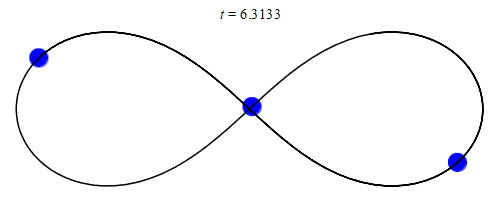 In 1993, a zero angular momentum solution with three equal masses moving around a figure-eight shape was discovered numerically by physicist Cris Moore at the Santa Fe Institute. Its formal existence was later proved in 2000 by mathematicians Alain Chenciner and Richard Montgomery. The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible that such orbits could be observed in the physical universe. However, it has been argued that this occurrence is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event resulting in a figure-8 orbit has been estimated to be a small fraction of 1%.
In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem. This was followed in 2018 by an additional 1223 new solutions for a zero-angular-momentum system of unequal masses.
In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three body problem. The free fall formulation of the three body problem starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forwards and backwards along an open "track".
In 1993, a zero angular momentum solution with three equal masses moving around a figure-eight shape was discovered numerically by physicist Cris Moore at the Santa Fe Institute. Its formal existence was later proved in 2000 by mathematicians Alain Chenciner and Richard Montgomery. The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible that such orbits could be observed in the physical universe. However, it has been argued that this occurrence is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event resulting in a figure-8 orbit has been estimated to be a small fraction of 1%.
In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem. This was followed in 2018 by an additional 1223 new solutions for a zero-angular-momentum system of unequal masses.
In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three body problem. The free fall formulation of the three body problem starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forwards and backwards along an open "track".
Physicists Discover a Whopping 13 New Solutions to Three-Body Problem
(''Science'')
3body simulator
- an example of a computer program that solves the three-body problem numerically {{Chaos theory Chaotic maps Classical mechanics Dynamical systems Mathematical physics Orbits Equations of astronomy
 In
In physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
and classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classi ...
, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in moti ...
and Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distan ...
. The three-body problem is a special case of the -body problem. Unlike two-body problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each ...
s, no general closed-form solution
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th roo ...
exists, as the resulting dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in ...
is chaotic
Chaotic was originally a Danish trading card game. It expanded to an online game in America which then became a television program based on the game. The program was able to be seen on 4Kids TV (Fox affiliates, nationwide), Jetix, The CW4Kid ...
for most initial conditions, and numerical methods are generally required.
Historically, the first specific three-body problem to receive extended study was the one involving the Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width of ...
, Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
, and the Sun
The Sun is the star at the center of the Solar System. It is a nearly perfect ball of hot plasma, heated to incandescence by nuclear fusion reactions in its core. The Sun radiates this energy mainly as light, ultraviolet, and infrared radi ...
. In an extended modern sense, a three-body problem is any problem in classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classi ...
or quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
that models the motion of three particles.
Mathematical description
The mathematical statement of the three-body problem can be given in terms of the Newtonian equations of motion for vector positions of three gravitationally interacting bodies with masses : : where is the gravitational constant. This is a set of nine second-order differential equations. The problem can also be stated equivalently in the Hamiltonian formalism, in which case it is described by a set of 18 first-order differential equations, one for each component of the positions and momenta : : where is theHamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
:
:
In this case is simply the total energy of the system, gravitational plus kinetic.
Restricted three-body problem
 In the ''restricted three-body problem'', a body of negligible mass (the "planetoid") moves under the influence of two massive bodies. Having negligible mass, the force that the planetoid exerts on the two massive bodies may be neglected, and the system can be analysed and can therefore be described in terms of a two-body motion. Usually this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.
The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem.
Mathematically, the problem is stated as follows. Let be the masses of the two massive bodies, with (planar) coordinates and , and let be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to . Then, the motion of the planetoid is given by
:
where . In this form the equations of motion carry an explicit time dependence through the coordinates . However, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.
In the ''restricted three-body problem'', a body of negligible mass (the "planetoid") moves under the influence of two massive bodies. Having negligible mass, the force that the planetoid exerts on the two massive bodies may be neglected, and the system can be analysed and can therefore be described in terms of a two-body motion. Usually this two-body motion is taken to consist of circular orbits around the center of mass, and the planetoid is assumed to move in the plane defined by the circular orbits.
The restricted three-body problem is easier to analyze theoretically than the full problem. It is of practical interest as well since it accurately describes many real-world problems, the most important example being the Earth–Moon–Sun system. For these reasons, it has occupied an important role in the historical development of the three-body problem.
Mathematically, the problem is stated as follows. Let be the masses of the two massive bodies, with (planar) coordinates and , and let be the coordinates of the planetoid. For simplicity, choose units such that the distance between the two massive bodies, as well as the gravitational constant, are both equal to . Then, the motion of the planetoid is given by
:
where . In this form the equations of motion carry an explicit time dependence through the coordinates . However, this time dependence can be removed through a transformation to a rotating reference frame, which simplifies any subsequent analysis.
Solutions
General solution
 There is no general
There is no general closed-form solution
In mathematics, a closed-form expression is a mathematical expression that uses a finite number of standard operations. It may contain constants, variables, certain well-known operations (e.g., + − × ÷), and functions (e.g., ''n''th roo ...
to the three-body problem, meaning there is no general solution that can be expressed in terms of a finite number of standard mathematical operations. Moreover, the motion of three bodies is generally non-repeating, except in special cases.
However, in 1912 the Finnish
Finnish may refer to:
* Something or someone from, or related to Finland
* Culture of Finland
* Finnish people or Finns, the primary ethnic group in Finland
* Finnish language, the national language of the Finnish people
* Finnish cuisine
See also ...
mathematician Karl Fritiof Sundman
Karl Frithiof Sundman (28 October 1873, in Kaskinen – 28 September 1949, in Helsinki) was a Finnish mathematician who used analytic methods to prove the existence of a convergent infinite series solution to the three-body problem in two papers p ...
proved that there exists an analytic solution to the three-body problem in the form of a power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a con ...
in terms of powers of . This series converges for all real , except for initial conditions corresponding to zero angular momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed syst ...
. In practice, the latter restriction is insignificant since initial conditions with zero angular momentum are rare, having Lebesgue measure zero.
An important issue in proving this result is the fact that the radius of convergence for this series is determined by the distance to the nearest singularity. Therefore, it is necessary to study the possible singularities of the three-body problems. As will be briefly discussed below, the only singularities in the three-body problem are binary collisions (collisions between two particles at an instant) and triple collisions (collisions between three particles at an instant).
Collisions, whether binary or triple (in fact, any number), are somewhat improbable, since it has been shown that they correspond to a set of initial conditions of measure zero. However, there is no criterion known to be put on the initial state in order to avoid collisions for the corresponding solution. So Sundman's strategy consisted of the following steps:
# Using an appropriate change of variables to continue analyzing the solution beyond the binary collision, in a process known as regularization
Regularization may refer to:
* Regularization (linguistics)
* Regularization (mathematics)
* Regularization (physics)
In physics, especially quantum field theory, regularization is a method of modifying observables which have singularities in ...
.
# Proving that triple collisions only occur when the angular momentum vanishes. By restricting the initial data to , he removed all ''real'' singularities from the transformed equations for the three-body problem.
# Showing that if , then not only can there be no triple collision, but the system is strictly bounded away from a triple collision. This implies, by using Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He w ...
's existence theorem for differential equations, that there are no complex singularities in a strip (depending on the value of ) in the complex plane centered around the real axis (shades of Kovalevskaya).
# Find a conformal transformation that maps this strip into the unit disc. For example, if (the new variable after the regularization) and if , then this map is given by
This finishes the proof of Sundman's theorem.
The corresponding series, however, converges very slowly. That is, obtaining a value of meaningful precision requires so many terms that this solution is of little practical use. Indeed, in 1930, David Beloriszky calculated that if Sundman's series were to be used for astronomical observations, then the computations would involve at least 10 terms.
Special-case solutions
In 1767,Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in ma ...
found three families of periodic solutions in which the three masses are collinear at each instant. See Euler's three-body problem
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space. This problem is exactly solvable, and yields an approxim ...
.
In 1772, Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. Together with Euler's collinear solutions, these solutions form the central configurations for the three-body problem. These solutions are valid for any mass ratios, and the masses move on Keplerian ellipses. These four families are the only known solutions for which there are explicit analytic formulae. In the special case of the circular restricted three-body problem, these solutions, viewed in a frame rotating with the primaries, become points which are referred to as L1, L2, L3, L4, and L5, and called Lagrangian points, with L4 and L5 being symmetric instances of Lagrange's solution.
In work summarized in 1892–1899, Henri Poincaré established the existence of an infinite number of periodic solutions to the restricted three-body problem, together with techniques for continuing these solutions into the general three-body problem.
In 1893, Meissel stated what is now called the Pythagorean three-body problem: three masses in the ratio 3:4:5 are placed at rest at the vertices of a 3:4:5 right triangle. Burrau further investigated this problem in 1913. In 1967 Victor Szebehely and C. Frederick Peters established eventual escape for this problem using numerical integration, while at the same time finding a nearby periodic solution.
In the 1970s, Michel Hénon and Roger A. Broucke each found a set of solutions that form part of the same family of solutions: the Broucke–Henon–Hadjidemetriou family. In this family the three objects all have the same mass and can exhibit both retrograde and direct forms. In some of Broucke's solutions two of the bodies follow the same path.
 In 1993, a zero angular momentum solution with three equal masses moving around a figure-eight shape was discovered numerically by physicist Cris Moore at the Santa Fe Institute. Its formal existence was later proved in 2000 by mathematicians Alain Chenciner and Richard Montgomery. The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible that such orbits could be observed in the physical universe. However, it has been argued that this occurrence is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event resulting in a figure-8 orbit has been estimated to be a small fraction of 1%.
In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem. This was followed in 2018 by an additional 1223 new solutions for a zero-angular-momentum system of unequal masses.
In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three body problem. The free fall formulation of the three body problem starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forwards and backwards along an open "track".
In 1993, a zero angular momentum solution with three equal masses moving around a figure-eight shape was discovered numerically by physicist Cris Moore at the Santa Fe Institute. Its formal existence was later proved in 2000 by mathematicians Alain Chenciner and Richard Montgomery. The solution has been shown numerically to be stable for small perturbations of the mass and orbital parameters, which makes it possible that such orbits could be observed in the physical universe. However, it has been argued that this occurrence is unlikely since the domain of stability is small. For instance, the probability of a binary–binary scattering event resulting in a figure-8 orbit has been estimated to be a small fraction of 1%.
In 2013, physicists Milovan Šuvakov and Veljko Dmitrašinović at the Institute of Physics in Belgrade discovered 13 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2015, physicist Ana Hudomal discovered 14 new families of solutions for the equal-mass zero-angular-momentum three-body problem.
In 2017, researchers Xiaoming Li and Shijun Liao found 669 new periodic orbits of the equal-mass zero-angular-momentum three-body problem. This was followed in 2018 by an additional 1223 new solutions for a zero-angular-momentum system of unequal masses.
In 2018, Li and Liao reported 234 solutions to the unequal-mass "free-fall" three body problem. The free fall formulation of the three body problem starts with all three bodies at rest. Because of this, the masses in a free-fall configuration do not orbit in a closed "loop", but travel forwards and backwards along an open "track".
Numerical approaches
Using a computer, the problem may be solved to arbitrarily high precision usingnumerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations ...
although high precision requires a large amount of CPU time. There have been attempts of creating computer programs that numerically solve the three-body problem (and by extension, the n-body problem) involving both electromagnetic and gravitational interactions, and incorporating modern theories of physics such as special relativity. In addition, using the theory of random walks
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space.
An elementary example of a random walk is the random walk on the integer number line \mathbb Z ...
, the probability of different outcomes may be computed.
History
The gravitational problem of three bodies in its traditional sense dates in substance from 1687, whenIsaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the grea ...
published his '' Philosophiæ Naturalis Principia Mathematica,'' when Newton was trying to figure out if any long term stability is possible, especially the system of our Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surfa ...
, the Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width of ...
, and the Sun. He was guided under the major Renaissance astronomers Nicolaus Copernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formulated ...
, Tycho Brahe
Tycho Brahe ( ; born Tyge Ottesen Brahe; generally called Tycho (14 December 154624 October 1601) was a Danish astronomer, known for his comprehensive astronomical observations, generally considered to be the most accurate of his time. He was ...
and Johannes Kepler to the beginning of the gravitational three-body problem. In Proposition 66 of Book 1 of the ''Principia'', and its 22 Corollaries, Newton took the first steps in the definition and study of the problem of the movements of three massive bodies subject to their mutually perturbing gravitational attractions. In Propositions 25 to 35 of Book 3, Newton also took the first steps in applying his results of Proposition 66 to the lunar theory, the motion of the Moon under the gravitational influence of Earth and the Sun. Later, this problem was also applied to other planets' interactions with the Earth and the Sun.
The physical problem was firstly addressed by Amerigo Vespucci and subsequently by Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He wa ...
, as well as Simon Stevin
Simon Stevin (; 1548–1620), sometimes called Stevinus, was a Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated vario ...
, but they did not realize what they contributed. Though Galileo determined that the speed of fall of all bodies changes uniformly and in the same way, he did not apply it to planetary motions. Whereas in 1499, Vespucci used knowledge of the position of the Moon to determine his position in Brazil. It became of technical importance in the 1720s, as an accurate solution would be applicable to navigation, specifically for the determination of longitude at sea, solved in practice by John Harrison
John Harrison ( – 24 March 1776) was a self-educated English carpenter and clockmaker who invented the marine chronometer, a long-sought-after device for solving the problem of calculating longitude while at sea.
Harrison's solution revol ...
's invention of the marine chronometer
A marine chronometer is a precision timepiece that is carried on a ship and employed in the determination of the ship's position by celestial navigation. It is used to determine longitude by comparing Greenwich Mean Time (GMT), or in the modern ...
. However the accuracy of the lunar theory was low, due to the perturbing effect of the Sun and planets on the motion of the Moon around Earth.
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert (; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the '' Encyclopéd ...
and Alexis Clairaut
Alexis Claude Clairaut (; 13 May 1713 – 17 May 1765) was a French mathematician, astronomer, and geophysicist. He was a prominent Newtonian whose work helped to establish the validity of the principles and results that Sir Isaac Newton had ou ...
, who developed a longstanding rivalry, both attempted to analyze the problem in some degree of generality; they submitted their competing first analyses to the Académie Royale des Sciences in 1747. It was in connection with their research, in Paris during the 1740s, that the name "three-body problem" (french: Problème des trois Corps) began to be commonly used. An account published in 1761 by Jean le Rond d'Alembert indicates that the name was first used in 1747.
From the end of the 19th century to early 20th century, the approach to solve the three-body problem with the usage of short-range attractive two-body forces was developed by scientists, which offered P.F. Bedaque, H.-W. Hammer and U. van Kolck an idea to renormalize the short-range three-body problem, providing scientists a rare example of a renormalization group
In theoretical physics, the term renormalization group (RG) refers to a formal apparatus that allows systematic investigation of the changes of a physical system as viewed at different scales. In particle physics, it reflects the changes in the ...
limit cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity o ...
at the beginning of the 21st century. George William Hill worked on the restricted problem in the late 19th century with an application of motion of Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never f ...
and Mercury.
At the beginning of the 20th century, Karl Sundman
Karl Frithiof Sundman (28 October 1873, in Kaskinen – 28 September 1949, in Helsinki) was a Finland, Finnish mathematician who used analytic methods to prove the existence of a convergent infinite series solution to the N-body problem#Three-body ...
approached the problem mathematically and systematically by providing a function theoretical proof to the problem valid for all values of time. It was the first time scientists theoretically solved three-body problem. However, because there was not enough qualitative solution of this system, and it was too slow for scientists to practically apply it, this solution still left some issues unresolved. In the 1970s, implication to three-body from two-body forces has been discovered by V. Efimov which was named as Efimov Effect Yefimov, sometimes spelled Efimov (russian: Ефимов), or Yefimova (feminine; Ефимова) is a Russian last name and may refer to:
* Alexander Yefimov (1923–2012), a Soviet aircraft pilot and twice Hero of the Soviet Union
* Boris Efimov ...
.
In 2017, Shijun Liao and Xiaoming Li applied a new strategy of numerical simulation for chaotic systems called the clean numerical simulation (CNS), with the use of a national supercomputer, to successfully gain 695 families of periodic solutions of the three-body system with equal mass.
In 2019, Breen et al. announced a fast neural network solver for the three-body problem, trained using a numerical integrator.
Other problems involving three bodies
The term "three-body problem" is sometimes used in the more general sense to refer to any physical problem involving the interaction of three bodies. A quantum-mechanical analogue of the gravitational three-body problem in classical mechanics is thehelium atom
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with either one or two neutrons, depending on the isotope, held together by ...
,
in which a helium
Helium (from el, ἥλιος, helios, lit=sun) is a chemical element with the symbol He and atomic number 2. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas and the first in the noble gas group in the periodic table. ...
nucleus and two electrons
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
interact according to the inverse-square Coulomb interaction
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is convention ...
. Like the
gravitational three-body problem, the helium atom cannot be solved exactly.
In both classical and quantum mechanics, however, there exist nontrivial interaction laws besides the inverse-square force which
do lead to exact analytic three-body solutions. One such model consists of a combination of harmonic attraction and a repulsive inverse-cube force. This model is considered nontrivial since it is associated with a set of nonlinear differential equations containing singularities (compared with, e.g., harmonic interactions alone, which lead to an easily solved system of linear differential equations). In these two respects it is analogous to (insoluble) models having Coulomb interactions, and as a result has been suggested as a tool for intuitively understanding physical systems like the helium atom.
The gravitational three-body problem has also been studied using general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
. Physically, a relativistic treatment becomes necessary in systems with very strong gravitational fields, such as near the event horizon
In astrophysics, an event horizon is a boundary beyond which events cannot affect an observer. Wolfgang Rindler coined the term in the 1950s.
In 1784, John Michell proposed that gravity can be strong enough in the vicinity of massive compact ob ...
of a black hole. However, the relativistic problem is considerably more difficult than in Newtonian mechanics, and sophisticated numerical techniques are required.
Even the full two-body problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each ...
(i.e. for arbitrary ratio of masses) does not have a rigorous analytic solution in general relativity.
-body problem
The three-body problem is a special case of the -body problem, which describes how objects move under one of the physical forces, such as gravity. These problems have a global analytical solution in the form of a convergent power series, as was proven by Karl F. Sundman for and byQiudong Wang
Qiudong Wang is a professor at the Department of Mathematics, the University of Arizona. In 1982 he received a B.S. at Nanjing University and in 1994 a Ph.D. at the University of Cincinnati.
Wang is best known for his 1991 paper ''The global so ...
for (see -body problem for details). However, the Sundman and Wang series converge so slowly that they are useless for practical purposes; therefore, it is currently necessary to approximate solutions by numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods ...
in the form of numerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations ...
or, for some cases, classical trigonometric series
In mathematics, a trigonometric series is a infinite series of the form
: \frac+\displaystyle\sum_^(A_ \cos + B_ \sin),
an infinite version of a trigonometric polynomial.
It is called the Fourier series of the integrable function f if the term ...
approximations (see -body simulation). Atomic systems, e.g. atoms, ions, and molecules, can be treated in terms of the quantum -body problem. Among classical physical systems, the -body problem usually refers to a galaxy or to a cluster of galaxies
A galaxy cluster, or a cluster of galaxies, is a structure that consists of anywhere from hundreds to thousands of galaxies that are bound together by gravity, with typical masses ranging from 1014 to 1015 solar masses. They are the second-lar ...
; planetary systems, such as stars, planets, and their satellites, can also be treated as -body systems. Some applications are conveniently treated by perturbation
Perturbation or perturb may refer to:
* Perturbation theory, mathematical methods that give approximate solutions to problems that cannot be solved exactly
* Perturbation (geology), changes in the nature of alluvial deposits over time
* Perturbat ...
theory, in which the system is considered as a two-body problem plus additional forces causing deviations from a hypothetical unperturbed two-body trajectory.
In popular culture
In the classic 1951 science-fiction film ''The Day the Earth Stood Still
''The Day the Earth Stood Still'' (a.k.a. ''Farewell to the Master'' and ''Journey to the World'') is a 1951 American science fiction film from 20th Century Fox, produced by Julian Blaustein and directed by Robert Wise. It stars Michael Re ...
'', the alien Klaatu, using the pseudonym Mr. Carpenter, makes some annotations to equations on Prof. Barnhardt's blackboard. Those equations are an accurate description of a particular form of the three-body problem.
The first volume of Chinese author Liu Cixin
Liu Cixin (, pronounced ; born 23 June 1963) is a Chinese science fiction writer. He is a nine-time winner of China's Galaxy Award and has also received the 2015 Hugo Award for his novel '' The Three-Body Problem'' as well as the 2017 Lo ...
's ''Remembrance of Earth's Past
''Remembrance of Earth's Past'' () is a science fiction series by Chinese writer Liu Cixin. The series is also popularly referred to as ''Three-Body'' from part of the title of its first novel, '' The Three-Body Problem'' (). The series details ...
'' trilogy is titled '' The Three-Body Problem'' and features the three-body problem as a central plot device.
See also
*Few-body systems
In mechanics, a few-body system consists of a small number of well-defined structures or point particles.
Quantum mechanics
In quantum mechanics, examples of few-body systems include light nuclear systems (that is, few-nucleon bound and scatter ...
* Galaxy formation and evolution
The study of galaxy formation and evolution is concerned with the processes that formed a heterogeneous universe from a homogeneous beginning, the formation of the first galaxies, the way galaxies change over time, and the processes that have gen ...
* Gravity assist
In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement (e.g. orbit around the Sun) and gravity of a planet or other astronomical object to alter the p ...
* Lagrange point
* Low-energy transfer
A low-energy transfer, or low-energy trajectory, is a route in space that allows spacecraft to change orbits using significantly less fuel than traditional transfers. These routes work in the Earth–Moon system and also in other systems, such as ...
* Michael Minovitch
* -body simulation
* Symplectic integrator In mathematics, a symplectic integrator (SI) is a numerical integration scheme for Hamiltonian systems. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations. They are widely used in ...
* Sitnikov problem
* Triple star system
A star system or stellar system is a small number of stars that orbit each other, bound by gravitational attraction. A large group of stars bound by gravitation is generally called a ''star cluster'' or ''galaxy'', although, broadly speaking, ...
References
Further reading
* * * * * * * * * *External links
*Physicists Discover a Whopping 13 New Solutions to Three-Body Problem
(''Science'')
3body simulator
- an example of a computer program that solves the three-body problem numerically {{Chaos theory Chaotic maps Classical mechanics Dynamical systems Mathematical physics Orbits Equations of astronomy