|
Zonoid
In convex geometry, a zonoid is a type of centrally symmetric convex body. Definitions The zonoids have several definitions, equivalent up to translations of the resulting shapes: * A zonoid is a shape that can be approximated arbitrarily closely (in Hausdorff distance) by a zonotope, a convex polytope formed from the Minkowski sum of finitely many line segments. In particular, every zonotope is a zonoid. Approximating a zonoid to within Hausdorff distance \varepsilon requires a number of segments that (for fixed \varepsilon) is near-linear in the dimension, or linear with some additional assumptions on the zonoid. * A zonoid is the range of an atom-free vector-valued sigma-additive set function. Here, a function from a family of sets to vectors is sigma-additive when the family is closed under countable disjoint unions, and when the value of the function on a union of sets equals the sum of its values on the sets. It is atom-free when every set whose function value is nonzero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lyapunov's Theorem
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of finite measure, which takes nonnegative real values only. Definitions and first consequences Given a field of sets (\Omega, \mathcal F) and a Banach space X, a finitely additive vector measure (or measure, for short) is a function \mu:\mathcal \to X such that for any two disjoint sets A and B in \mathcal one has \mu(A\cup B) =\mu(A) + \mu (B). A vector measure \mu is called countably additive if for any sequence (A_i)_^ of disjoint sets in \mathcal F such that their union is in \mathcal F it holds that \mu = \sum_^\mu(A_i) with the series on the right-hand side convergent in the norm of the Banach space X. It can be proved that an additive vector measure \mu is countably additive if and only if for any sequence (A_i)_^ as above one has where \, \cdot\, is the norm on X. Countably additive vector measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Geometry
In mathematics, convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space. Convex sets occur naturally in many areas: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming, probability theory, game theory, etc. Classification According to the Mathematics Subject Classification MSC2010, the mathematical discipline ''Convex and Discrete Geometry'' includes three major branches: * general convexity * polytopes and polyhedra * discrete geometry (though only portions of the latter two are included in convex geometry). General convexity is further subdivided as follows: *axiomatic and generalized convexity *convex sets without dimension restrictions *convex sets in topological vector spaces *convex sets in 2 dimensions (including convex curves) *convex sets in 3 dimensions (including convex surfaces) *convex sets in ''n'' dimensions (including convex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
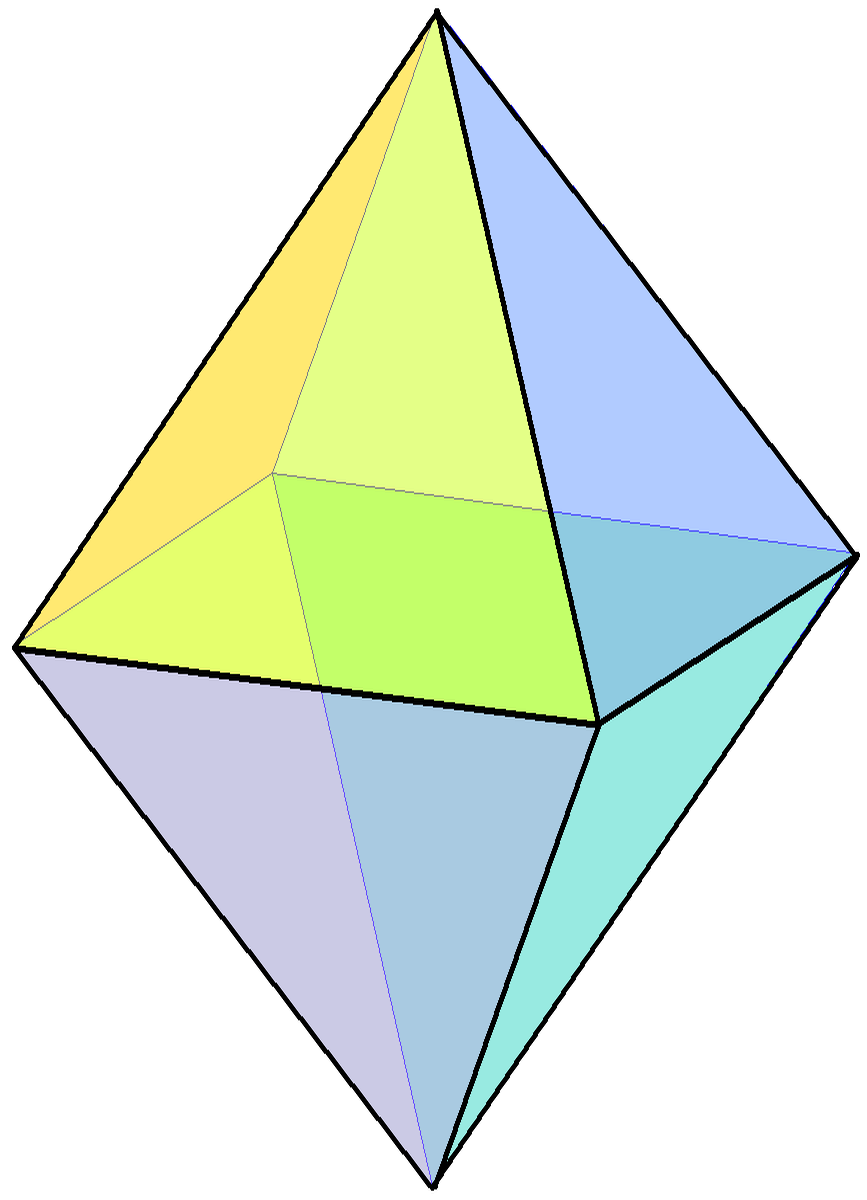
Regular Octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyhedron; many types of irregular octahedra also exist. A regular octahedron is convex, meaning that for any two points within it, the line segment connecting them lies entirely within it. It is one of the eight convex deltahedra because all of the faces are equilateral triangles. It is a composite polyhedron made by attaching two equilateral square pyramids. Its dual polyhedron is the cube, and they have the same three-dimensional symmetry groups, the octahedral symmetry \mathrm_\mathrm . A regular octahedron is a special case of an octahedron, any eight-sided polyhedron. It is the three-dimensional case of the more general concept of a cross-polytope. As a Platonic solid The regular octahedron is one of the Platonic solids, a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The American Mathematical Monthly
''The American Mathematical Monthly'' is a peer-reviewed scientific journal of mathematics. It was established by Benjamin Finkel in 1894 and is published by Taylor & Francis on behalf of the Mathematical Association of America. It is an expository journal intended for a wide audience of mathematicians, from undergraduate students to research professionals. Articles are chosen on the basis of their broad interest and reviewed and edited for quality of exposition as well as content. The editor-in-chief is Vadim Ponomarenko (San Diego State University). The journal gives the Lester R. Ford Award annually to "authors of articles of expository excellence" published in the journal. Editors-in-chief The following persons are or have been editor-in-chief: See also *''Mathematics Magazine'' *''Notices of the American Mathematical Society ''Notices of the American Mathematical Society'' is the membership journal of the American Mathematical Society (AMS), published monthly except f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transactions Of The American Mathematical Society
The ''Transactions of the American Mathematical Society'' is a monthly peer-reviewed scientific journal of pure and applied mathematics published by the American Mathematical Society. It was established in 1900. As a requirement, all articles must be more than 15 printed pages. Its ISSN number is 0002-9947. See also * ''Bulletin of the American Mathematical Society'' * ''Journal of the American Mathematical Society'' * '' Memoirs of the American Mathematical Society'' * '' Notices of the American Mathematical Society'' * ''Proceedings of the American Mathematical Society'' References External links * ''Transactions of the American Mathematical Society''on JSTOR JSTOR ( ; short for ''Journal Storage'') is a digital library of academic journals, books, and primary sources founded in 1994. Originally containing digitized back issues of academic journals, it now encompasses books and other primary source ... American Mathematical Society academic journals Mathematics jo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilhelm Blaschke
Wilhelm Johann Eugen Blaschke (13 September 1885 – 17 March 1962) was an Austrian mathematician working in the fields of differential and integral geometry. Education and career Blaschke was the son of mathematician Josef Blaschke, who taught geometry at the Landes Oberrealschule in Graz. After studying for two years at the Technische Hochschule in Graz, he went to the University of Vienna, and completed a doctorate in 1908 under the supervision of Wilhelm Wirtinger. His dissertation was ''Über eine besondere Art von Kurven vierter Klasse''. After completing his doctorate he spent several years visiting mathematicians at the major universities in Italy and Germany. He spent two years each in positions in Prague, Leipzig, Göttingen, and Tübingen until, in 1919, he took the professorship at the University of Hamburg that he would keep for the rest of his career. His students at Hamburg included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner. In 1933 Blaschke sign ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homothety
In mathematics, a homothety (or homothecy, or homogeneous dilation) is a transformation of an affine space determined by a point called its ''center'' and a nonzero number called its ''ratio'', which sends point to a point by the rule, : \overrightarrow=k\overrightarrow for a fixed number k\ne 0. Using position vectors: :\mathbf x'=\mathbf s + k(\mathbf x -\mathbf s). In case of S=O (Origin): :\mathbf x'=k\mathbf x, which is a uniform scaling and shows the meaning of special choices for k: :for k=1 one gets the ''identity'' mapping, :for k=-1 one gets the ''reflection'' at the center, For 1/k one gets the ''inverse'' mapping defined by k. In Euclidean geometry homotheties are the similarities that fix a point and either preserve (if k>0) or reverse (if k<0) the direction of all vectors. Together with the translations, all homotheties of an affine (or Euclid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Projection
In three-dimensional geometry, a parallel projection (or axonometric projection) is a projection of an object in three-dimensional space onto a fixed plane, known as the ''projection plane'' or ''image plane'', where the '' rays'', known as '' lines of sight'' or ''projection lines'', are parallel to each other. It is a basic tool in descriptive geometry. The projection is called '' orthographic'' if the rays are perpendicular (orthogonal) to the image plane, and '' oblique'' or '' skew'' if they are not. Overview A parallel projection is a particular case of ''projection'' in mathematics and ''graphical projection'' in technical drawing. Parallel projections can be seen as the limit of a central or perspective projection, in which the rays pass through a fixed point called the ''center'' or ''viewpoint'', as this point is moved towards infinity. Put differently, a parallel projection corresponds to a perspective projection with an infinite focal length (the distance between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, '' affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicone
In geometry, a bicone or dicone (from , and Greek: ''di-'', both meaning "two") is the three-dimensional surface of revolution of a rhombus around one of its axes of symmetry. Equivalently, a bicone is the surface created by joining two congruent right circular cones at their bases. A bicone has circular symmetry and orthogonal bilateral symmetry. Geometry For a bicone with radius r and half-height h, the volume is :V = \frac \pi r^2 h and the surface area is :A =2\pi r \ell\, where :\ell = \sqrt is the slant height. See also * Sphericon In solid geometry, the sphericon is a solid that has a continuous developable surface with two Congruence (geometry), congruent, semicircle, semi-circular edges, and four Vertex (geometry), vertices that define a square. It is a member of a spe ... * Biconical antenna References External links * Elementary geometry Surfaces {{Elementary-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sine Curve
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is '' simple harmonic motion''; as rotation, it corresponds to '' uniform circular motion''. Sine waves occur often in physics, including wind waves, sound waves, and light waves, such as monochromatic radiation. In engineering, signal processing, and mathematics, Fourier analysis decomposes general functions into a sum of sine waves of various frequencies, relative phases, and magnitudes. When any two sine waves of the same frequency (but arbitrary phase) are linearly combined, the result is another sine wave of the same frequency; this property is unique among periodic waves. Conversely, if some phase is chosen as a zero reference, a sine wave of arbitrary phase can be written as the linear combination of two sine waves with phases of zero and a quarter cycle, the ''sine'' and ''cosine'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a Solid geometry, solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution''), which may not Intersection (geometry), intersect the generatrix (except at its boundary). The Surface (mathematics), surface created by this revolution and which bounds the solid is the ''surface of revolution''. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area (Pappus's centroid theorem, Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylinder (geometry), cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the Disc integration, disc met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |