|
Wild Knot
In the mathematical theory of knots, a knot is tame if it can be "thickened", that is, if there exists an extension to an embedding of the solid torus S^1\times D^2 into the 3-sphere. A knot is tame if and only if it can be represented as a finite closed polygonal chain. In knot theory and 3-manifold theory, often the adjective "tame" is omitted. Smooth knots, for example, are always tame. Knots that are not tame are called wild and can have pathological behavior. Every closed curve containing a wild arc is a wild knot. It has been conjectured that every wild knot has infinitely many quadrisecants. As well as their mathematical study, wild knots have also been studied for their potential for decorative purposes in Celtic-style ornamental knotwork. See also * Wild arc In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
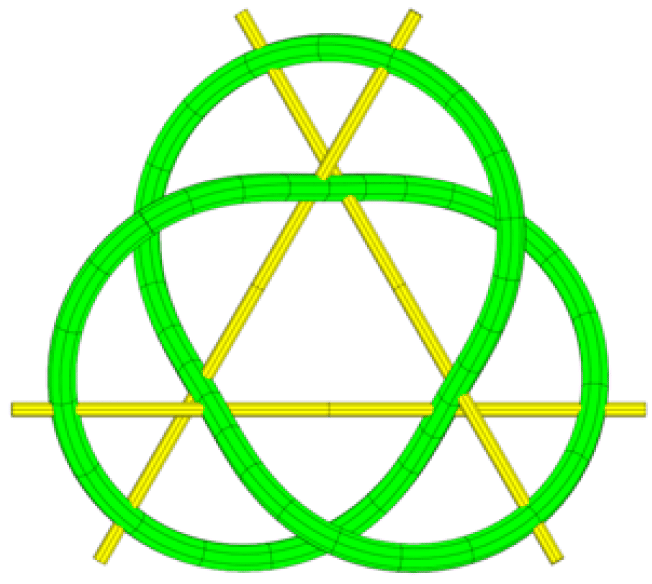
Quadrisecant
In geometry, a quadrisecant or quadrisecant line of a space curve is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types: * Knots and links in knot theory, when nontrivial, always have quadrisecants, and the existence and number of quadrisecants has been studied in connection with knot invariants including the minimum total curvature and the ropelength of a knot. *The number of quadrisecants of a non-singular algebraic curve in complex projective space can be computed by a formula derived by Arthur Cayley. *Quadrisecants of arrangements of skew lines touch subsets of four lines from the arrangement. They are associated with ruled surfaces and the Schläfli double six configuration. Definition and motivation A quadrisecant is a line that intersects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eilenberg–Mazur Swindle
In mathematics, the Eilenberg–Mazur swindle, named after Samuel Eilenberg and Barry Mazur, is a method of proof that involves paradoxical properties of infinite sums. In geometric topology it was introduced by and is often called the Mazur swindle. In algebra it was introduced by Samuel Eilenberg and is known as the Eilenberg swindle or Eilenberg telescope (see telescoping sum). The Eilenberg–Mazur swindle is similar to the following well known joke "proof" that 1 = 0: : 1 = 1 + (−1 + 1) + (−1 + 1) + ... = 1 − 1 + 1 − 1 + ... = (1 − 1) + (1 − 1) + ... = 0 This "proof" is not valid as a claim about real numbers because Grandi's series 1 − 1 + 1 − 1 + ... does not converge, but the analogous argument can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexander Horned Sphere
The Alexander horned sphere is a pathological object in topology discovered by . It is a particular topological embedding of a two-dimensional sphere in three-dimensional space. Together with its inside, it is a topological 3-ball, the Alexander horned ball, and so is simply connected; i.e., every loop can be shrunk to a point while staying inside. However, the exterior is ''not'' simply connected, unlike the exterior of the usual round sphere. Construction The Alexander horned sphere is the particular (topological) embedding of a sphere in 3-dimensional Euclidean space obtained by the following construction, starting with a standard torus:. #Remove a radial slice of the torus. #Connect a standard punctured torus to each side of the cut, interlinked with the torus on the other side. #Repeat steps 1–2 on the two tori just added ''ad infinitum''. By considering only the points of the tori that are not removed at some stage, an embedding of the sphere with a Cantor set remov ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wild Arc
In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment. found the first example of a wild arc. found another example, called the Fox-Artin arc, whose complement is not simply connected. Fox-Artin arcs Two very similar wild arcs appear in the article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right. The left end-point 0 of the closed unit interval ,1/math> is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space \mathbb^3 or the 3-sphere S^3. Fox-Artin arc variant Example 1.1* has the crossing sequence over/under/over/under/over/under. According to , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Decorative Knots
A decorative or ornamental knot (also fancy knot) is an often complex knot exhibiting repeating patterns. A decorative arts, decorative knot is generally a knot that not only has practical use but is also known for its beauty, aesthetic or ornament (art), ornamental qualities.Owen (1994), p.125. Access date: 2010-02-18. "They can be used for practical purposes or pure decoration. Often originating from maritime use, "decorative knots are not only serviceable and functional but also enhance the ship-shape appearance of any vessel." Decorative knots may be used alone or in combination, and may consist of single or multiple strands.Penn, Randy (2004). ''The Everything Knots Book: Step-By-Step Instructions for Tying Any Knot'', p.189. Everything Books. .Randall, Peter (20 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celtic Knot
Celtic knots (, , , ) are a variety of knots and Style (visual arts)#Stylization, stylized graphical representations of knots used for decoration, used extensively in the Celtic style of Insular art. These knots are most known for their adaptation for use in the ornament (architecture), ornamentation of Christian monuments and manuscripts, such as the 8th-century St. Teilo Gospels, the Book of Kells and the Lindisfarne Gospels. Most are endless knots, and many are varieties of basket weave knots. History The use of interlace (visual arts), interlace patterns had its origins in the late Roman Empire. Knot patterns first appeared in the third and fourth centuries AD and can be seen in Roman floor mosaics of that time. Interesting developments in the artistic use of interlaced knot patterns are found in Byzantine architecture and Illuminated manuscript, book illumination, Coptic art, Celtic art, Islamic art, Kievan Rus' book illumination, Ethiopian art, and European architecture ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Knot Theory And Its Ramifications
The ''Journal of Knot Theory and Its Ramifications'' was established in 1992 by Louis Kauffman and was the first journal purely devoted to knot theory. It is an interdisciplinary journal covering developments in knot theory, with emphasis on creating connections between with other branches of mathematics and the natural sciences. The journal is published by World Scientific. , retrieved 2015-03-02. According to the '''', the journal has a 2020 |
Wild Arc
In geometric topology, a wild arc is an embedding of the unit interval into 3-dimensional space not equivalent to the usual one in the sense that there does not exist an ambient isotopy taking the arc to a straight line segment. found the first example of a wild arc. found another example, called the Fox-Artin arc, whose complement is not simply connected. Fox-Artin arcs Two very similar wild arcs appear in the article. Example 1.1 (page 981) is most generally referred to as the Fox-Artin wild arc. The crossings have the regular sequence over/over/under/over/under/under when following the curve from left to right. The left end-point 0 of the closed unit interval ,1/math> is mapped by the arc to the left limit point of the curve, and 1 is mapped to the right limit point. The range of the arc lies in the Euclidean space \mathbb^3 or the 3-sphere S^3. Fox-Artin arc variant Example 1.1* has the crossing sequence over/under/over/under/over/under. According to , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Knot Theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring (or "unknot"). In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, \mathbb^3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of \mathbb^3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself. Knots can be described in various ways. Using different description methods, there may be more than one description of the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram, in which any knot can be drawn in many different ways. Therefore, a fundamental p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pathological (mathematics)
In mathematics, when a mathematical phenomenon runs counter to some intuition, then the phenomenon is sometimes called pathological. On the other hand, if a phenomenon does not run counter to intuition, it is sometimes called well-behaved or nice. These terms are sometimes useful in mathematical research and teaching, but there is no strict mathematical definition of pathological or well-behaved. In analysis A classic example of a pathology is the Weierstrass function, a function that is continuous everywhere but differentiable nowhere. The sum of a differentiable function and the Weierstrass function is again continuous but nowhere differentiable; so there are at least as many such functions as differentiable functions. In fact, using the Baire category theorem, one can show that continuous functions are generically nowhere differentiable. Such examples were deemed pathological when they were first discovered. To quote Henri Poincaré: Since Poincaré, nowhere differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-manifold
In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane (geometry), plane (a tangent plane) to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Principles Definition A topological space M is a 3-manifold if it is a second-countable Hausdorff space and if every point in M has a neighbourhood (mathematics), neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, Piecewise linear manifold, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |