|
Transport Phenomena
In engineering, physics, and chemistry, the study of transport phenomena concerns the exchange of mass, energy, charge, momentum and angular momentum between observed and studied systems. While it draws from fields as diverse as continuum mechanics and thermodynamics, it places a heavy emphasis on the commonalities between the topics covered. Mass, momentum, and heat transport all share a very similar mathematical framework, and the parallels between them are exploited in the study of transport phenomena to draw deep mathematical connections that often provide very useful tools in the analysis of one field that are directly derived from the others. The fundamental analysis in all three subfields of mass, heat, and momentum transfer are often grounded in the simple principle that the total sum of the quantities being studied must be conserved by the system and its environment. Thus, the different phenomena that lead to transport are each considered individually with the knowledge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more specialized List of engineering branches, fields of engineering, each with a more specific emphasis on particular areas of applied mathematics, applied science, and types of application. See glossary of engineering. The term ''engineering'' is derived from the Latin ''ingenium'', meaning "cleverness" and ''ingeniare'', meaning "to contrive, devise". Definition The American Engineers' Council for Professional Development (ECPD, the predecessor of Accreditation Board for Engineering and Technology, ABET) has defined "engineering" as: The creative application of scientific principles to design or develop structures, machines, apparatus, or manufacturing processes, or works utilizing them singly or in combination; or to construct o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Change
Physical changes are changes affecting the form of a chemical substance, but not its chemical composition. Physical changes are used to separate mixtures into their component compounds, but can not usually be used to separate compounds into chemical elements or simpler compounds.Zumdahl, Steven S. and Zumdahl, Susan A. (2000), ''Chemistry,'' Houghton Mifflin, 5th ed., p. 27 Physical changes occur when objects or substances undergo a change that does not change their chemical composition. This contrasts with the concept of chemical change in which the composition of a substance changes or one or more substances combine or break up to form new substances. In general a physical change is reversible using physical means. For example, salt dissolved in water can be recovered by allowing the water to evaporate. A physical change involves a change in physical properties. Examples of physical properties include melting, transition to a gas, change of strength, change of durability, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
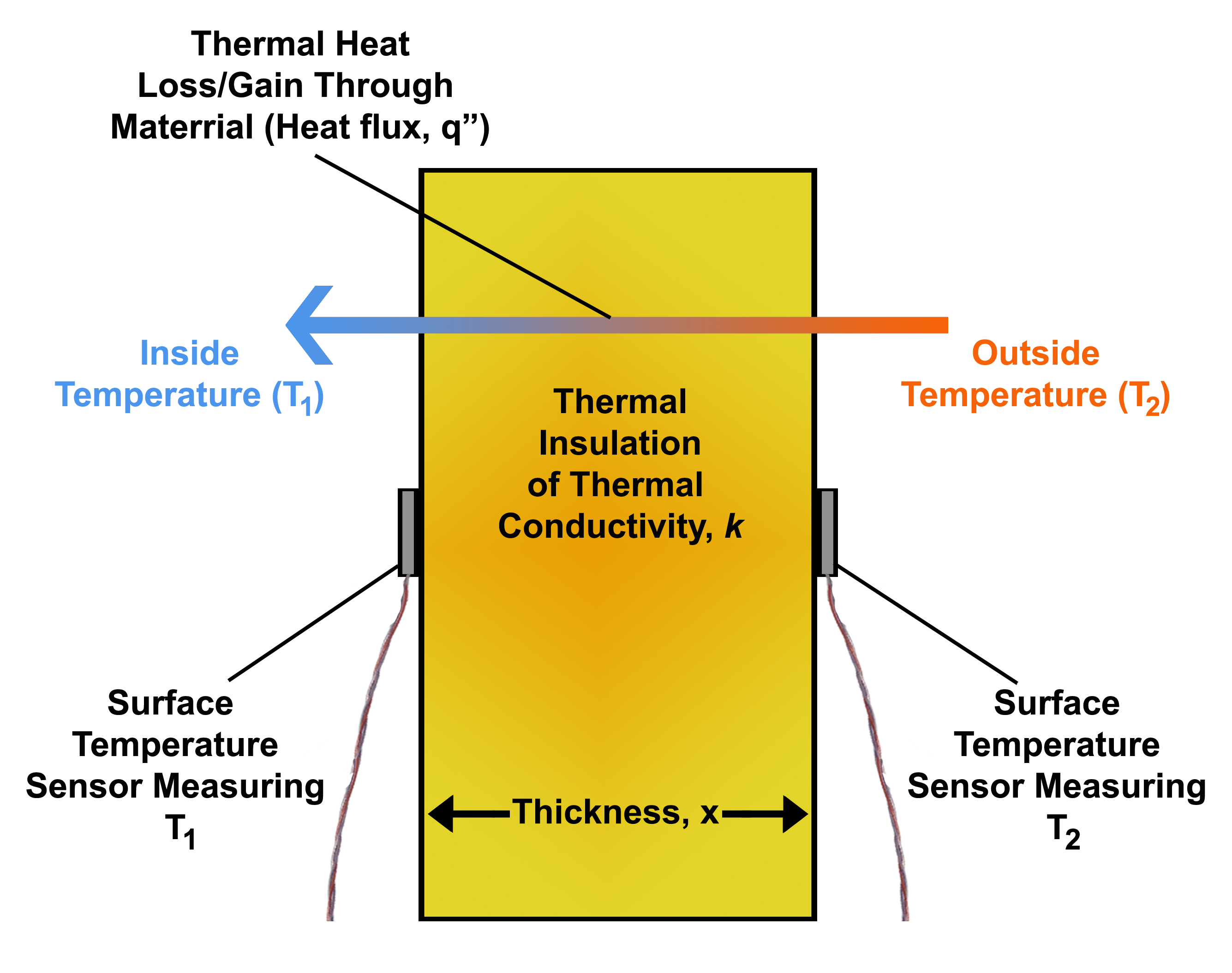
Heat Flux
Heat flux or thermal flux, sometimes also referred to as ''heat flux density'', heat-flow density or ''heat flow rate intensity'' is a flow of energy per unit area per unit time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small. Heat flux is often denoted \vec_\mathrm, the subscript specifying ''heat'' flux, as opposed to ''mass'' or ''momentum'' flux. Fourier's law is an important application of these concepts. Fourier's law For most solids in usual conditions, heat is transported mainly by conduction and the heat flux is adequately described by Fourier's law. Fourier's law in one dimension \phi_\text = -k \frac where k is the thermal conductivity. The negative sign shows that heat flux moves from higher temperature regions to lower temperature regions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Navier–Stokes Equations
In physics, the Navier–Stokes equations ( ) are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Anglo-Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes). The Navier–Stokes equations mathematically express conservation of momentum and conservation of mass for Newtonian fluids. They are sometimes accompanied by an equation of state relating pressure, temperature and density. They arise from applying Isaac Newton's second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscous term (proportional to the gradient of velocity) and a pressure term—hence describing ''viscous flow''. The difference between them and the closely related Euler equations is that Navier–Stokes equations take ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier's Law
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its ''thermal conductivity'', and is denoted . Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform. In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which may be separated spatially. Heat can also be transferred by a combination of conduction and radiation. In solids, conduction is mediated by the combination of vibrations and collisions of molecul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constitutive Equations
In physics and engineering, a constitutive equation or constitutive relation is a relation between two physical quantities (especially kinetic quantities as related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external stimuli, usually as applied fields or forces. They are combined with other equations governing physical laws to solve physical problems; for example in fluid mechanics the flow of a fluid in a pipe, in solid state physics the response of a crystal to an electric field, or in structural analysis, the connection between applied stresses or loads to strains or deformations. Some constitutive equations are simply phenomenological; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, it is o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuity Equations
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constitutive Equation
In physics and engineering, a constitutive equation or constitutive relation is a relation between two physical quantities (especially kinetic quantities as related to kinematic quantities) that is specific to a material or substance, and approximates the response of that material to external stimuli, usually as applied fields or forces. They are combined with other equations governing physical laws to solve physical problems; for example in fluid mechanics the flow of a fluid in a pipe, in solid state physics the response of a crystal to an electric field, or in structural analysis, the connection between applied stresses or loads to strains or deformations. Some constitutive equations are simply phenomenological; others are derived from first principles. A common approximate constitutive equation frequently is expressed as a simple proportionality using a parameter taken to be a property of the material, such as electrical conductivity or a spring constant. However, it i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Law (physics)
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all. A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume. From Noether's theorem, each conservation law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecules
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and biochemistry, the distinction from ions is dropped and ''molecule'' is often used when referring to polyatomic ions. A molecule may be homonuclear, that is, it consists of atoms of one chemical element, e.g. two atoms in the oxygen molecule (O2); or it may be heteronuclear, a chemical compound composed of more than one element, e.g. water (molecule), water (two hydrogen atoms and one oxygen atom; H2O). In the kinetic theory of gases, the term ''molecule'' is often used for any gaseous particle regardless of its composition. This relaxes the requirement that a molecule contains two or more atoms, since the noble gases are individual atoms. Atoms and complexes connected by non-covalent interactions, such as hydrogen bonds or ionic bonds, are typic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behavior of nature from the behavior of such ensembles. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. This established the fields of statistical thermodynamics and statistical physics. The founding of the field of statistical mechanics is generally credited to three physicists: *Ludwig Boltzmann, who developed the fundamental interpretation of entropy in terms of a collection of microstates *James Clerk Maxwell, who developed models of probability distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reversible Process (thermodynamics)
In thermodynamics, a reversible process is a process, involving a system and its surroundings, whose direction can be reversed by infinitesimal changes in some properties of the surroundings, such as pressure or temperature. Throughout an entire reversible process, the system is in thermodynamic equilibrium, both physical and chemical, and ''nearly'' in pressure and temperature equilibrium with its surroundings. This prevents unbalanced forces and acceleration of moving system boundaries, which in turn avoids friction and other dissipation. To maintain equilibrium, reversible processes are extremely slow ( ''quasistatic''). The process must occur slowly enough that after some small change in a thermodynamic parameter, the physical processes in the system have enough time for the other parameters to self-adjust to match the new, changed parameter value. For example, if a container of water has sat in a room long enough to match the steady temperature of the surrounding air, for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |