|
Time Scale Calculus
In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid systems. It has applications in any field that requires simultaneous modelling of Discrete time and continuous time, discrete and continuous data. It gives a new definition of a derivative such that if one differentiates a function defined on the real numbers then the definition is equivalent to standard differentiation, but if one uses a function defined on the integers then it is equivalent to the forward difference operator. History Time-scale calculus was introduced in 1988 by the German mathematician Stefan Hilger. However, similar ideas have been used before and go back at least to the introduction of the Riemann–Stieltjes integral, which unifies sums and integrals. Dynamic equations Many results concerning differential e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Cantor Set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883. Through consideration of this set, Cantor and others helped lay the foundations of modern point-set topology. The most common construction is the Cantor ternary set, built by removing the middle third of a line segment and then repeating the process with the remaining shorter segments. Cantor mentioned this ternary construction only in passing, as an example of a perfect set that is nowhere dense. More generally, in topology, a Cantor space is a topological space homeomorphic to the Cantor ternary set (equipped with its subspace topology). The Cantor set is naturally homeomorphic to the countable product ^ of the discrete two-point space \underline 2 . By a theorem of L. E. J. Brouwer, this is equivalent to being perfect, nonempty, compac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Forward Difference Operator
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation. The difference operator, commonly denoted \Delta, is the operator that maps a function to the function \Delta /math> defined by \Delta x) = f(x+1)-f(x). A difference equation is a functional equation that involves the finite difference operator in the same way as a differential equation involves derivatives. There are many similarities between difference equations and differential equations. Certain recurrence relations can be written as difference equations by replacing iteration notation with finite differences. In numerical analysis, finite differences are widely used for approximating derivatives, and the term "finite difference" is often used as an abbreviation of "finite difference approximation of derivatives". Finite differences were introduced by Brook Taylo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Banach Space
In mathematics, more specifically in functional analysis, a Banach space (, ) is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well-defined limit that is within the space. Banach spaces are named after the Polish mathematician Stefan Banach, who introduced this concept and studied it systematically in 1920–1922 along with Hans Hahn and Eduard Helly. Maurice René Fréchet was the first to use the term "Banach space" and Banach in turn then coined the term " Fréchet space". Banach spaces originally grew out of the study of function spaces by Hilbert, Fréchet, and Riesz earlier in the century. Banach spaces play a central role in functional analysis. In other areas of analysis, the spaces under study are often Banach spaces. Definition A Banach space is a complete nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
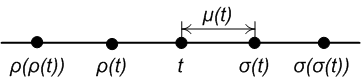
Timescales Point Classifications
Time scale may refer to: *Time standard, a specification of either the rate at which time passes, points in time, or both *A duration or quantity of time: ** Orders of magnitude (time) as a power of 10 in seconds; **A specific unit of time *Geological time scale, a scale that divides up the history of Earth into scientifically meaningful periods In astronomy and physics: * Dynamical time scale, in stellar physics, the time in which changes in one part of a body can be communicated to the rest of that body, or in celestial mechanics, a realization of a time-like argument based on a dynamical theory * Nuclear timescale, an estimate of the lifetime of a star based solely on its rate of fuel consumption * Thermal time scale, an estimate of the lifetime of a star once the fuel reserves at its center are used up In cosmology and particle physics: *Planck time, the time scale beneath which quantum effects are comparable in significance to gravitational effects In mathematics: * Time-sca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |