|
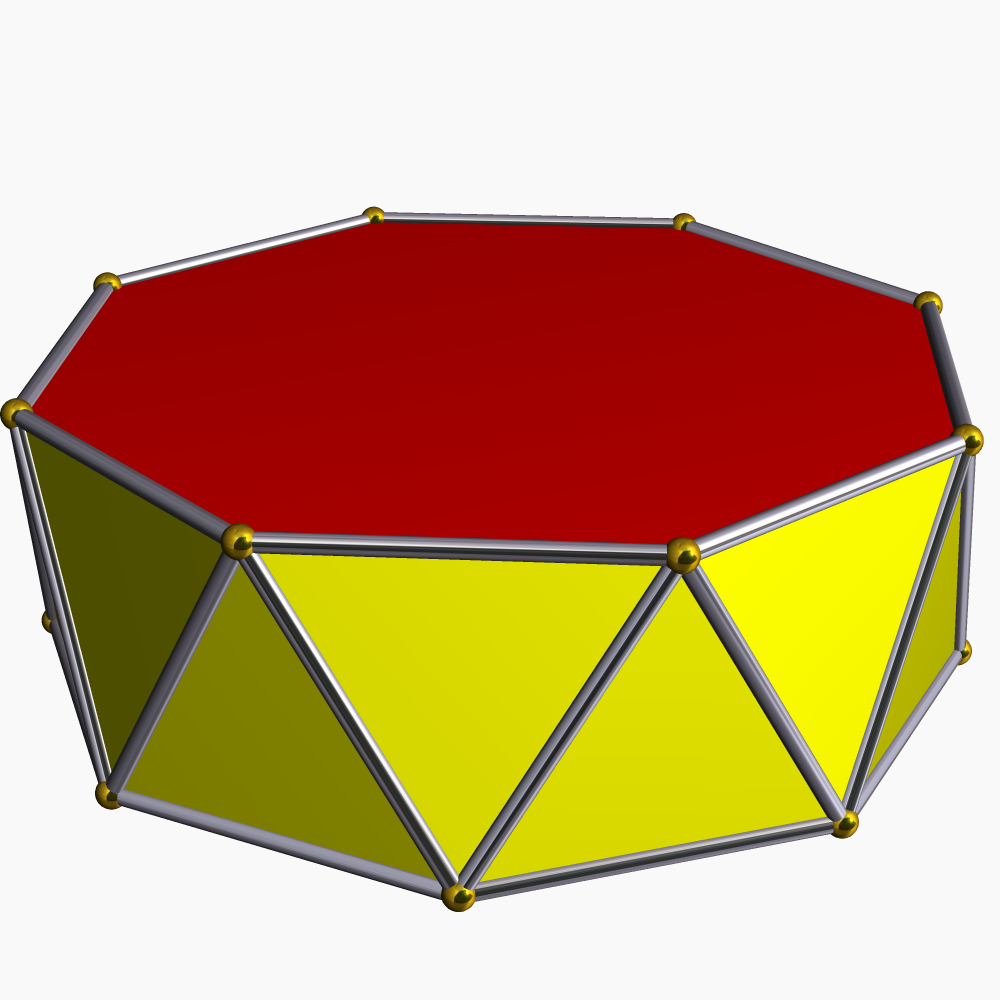
Triangular Prisms
In geometry, a triangular prism or trigonal prism is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a ''right triangular prism''. A right triangular prism may be both semiregular and uniform. The triangular prism can be used in constructing another polyhedron. Examples are some of the Johnson solids, the truncated right triangular prism, and Schönhardt polyhedron. Properties A triangular prism has 6 vertices, 9 edges, and 5 faces. Every prism has 2 congruent faces known as its ''bases'', and the bases of a triangular prism are triangles. The triangle has 3 vertices, each of which pairs with another triangle's vertex, making up another 3 edges. These edges form 3 parallelograms as other faces. If the prism's edges are perpendicular to the base, the lateral faces are rectangles, and the prism is called a ''right triangular prism''. This prism may also be considered a special case of a wedge. If ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism (geometry)
In geometry, a prism is a polyhedron comprising an polygon Base (geometry), base, a second base which is a Translation (geometry), translated copy (rigidly moved without rotation) of the first, and other Face (geometry), faces, necessarily all parallelograms, joining corresponding sides of the two bases. All Cross section (geometry), cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases, e.g. a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids. Like many basic geometric terms, the word ''prism'' () was first used in Euclid's Elements, Euclid's ''Elements''. Euclid defined the term in Book XI as "a solid figure contained by two opposite, equal and parallel planes, while the rest are parallelograms". However, this definition has been criticized for not being specific enough in regard to the nature of the bases (a cause of some confusion amongst generations of later geometry writers). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isogonal Figure
In geometry, a polytope (e.g. a polygon or polyhedron) or a Tessellation, tiling is isogonal or vertex-transitive if all its vertex (geometry), vertices are equivalent under the Symmetry, symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face (geometry), face in the same or reverse order, and with the same Dihedral angle, angles between corresponding faces. Technically, one says that for any two vertices there exists a symmetry of the polytope Map (mathematics), mapping the first isometry, isometrically onto the second. Other ways of saying this are that the automorphism group, group of automorphisms of the polytope ''Group action#Remarkable properties of actions, acts transitively'' on its vertices, or that the vertices lie within a single ''symmetry orbit''. All vertices of a finite -dimensional isogonal figure exist on an n-sphere, -sphere. The term isogonal has long been used for polyhedra. Vertex-transitive is a synonym borrowed fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Pyramid
In geometry, the elongated triangular pyramid is one of the Johnson solids (). As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base. Like any elongated pyramid, the resulting solid is topologically (but not geometrically) self- dual. Construction The elongated triangular pyramid is constructed from a triangular prism by attaching regular tetrahedron onto one of its bases, a process known as elongation. The tetrahedron covers an equilateral triangle, replacing it with three other equilateral triangles, so that the resulting polyhedron has four equilateral triangles and three squares as its faces. A convex polyhedron in which all of the faces are regular polygons is called the Johnson solid In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway polyhedron notation, Conway notation . Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron. Antiprisms are similar to Prism (geometry), prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are triangles, rather than quadrilaterals. The dual polyhedron of an -gonal antiprism is an -gonal trapezohedron. History In his 1619 book ''Harmonices Mundi'', Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net (geometry), net of a hexagonal antiprism has been attributed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalan Solid
The Catalan solids are the dual polyhedron, dual polyhedra of Archimedean solids. The Archimedean solids are thirteen highly-symmetric polyhedra with regular faces and symmetric vertices. The faces of the Catalan solids correspond by duality to the vertices of Archimedean solids, and vice versa. One way to construct the Catalan solids is by using the Dorman Luke construction. The Catalan solids are face-transitive or ''isohedral'' meaning that their faces are symmetric to one another, but they are not vertex-transitive because their vertices are not symmetric. Their dual, the Archimedean solids, are vertex-transitive but not face-transitive. Each Catalan solid has constant dihedral angles, meaning the angle between any two adjacent faces is the same. Additionally, two Catalan solids, the rhombic dodecahedron and rhombic triacontahedron, are edge-transitive, meaning their edges are symmetric to each other. Some Catalan solids were discovered by Johannes Kepler during his study of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedean Solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They belong to the class of uniform polyhedra, the polyhedra with regular faces and symmetric vertices. Some Archimedean solids were portrayed in the works of artists and mathematicians during the Renaissance. The elongated square gyrobicupola or ' is an extra polyhedron with regular faces and congruent vertices, but it is not generally counted as an Archimedean solid because it is not vertex-transitive. The solids The Archimedean solids have a single vertex configuration and highly symmetric properties. A vertex configuration indicates which regular polygons meet at each vertex. For instance, the configuration 3 \cdot 5 \cdot 3 \cdot 5 indicates a polyhedron in which each vertex is met by alternating two triangles and two pentagons. Highl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halin Graph
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree (graph theory), tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the Euclidean plane, plane so none of its edges cross (this is called a planar embedding), and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.''Encyclopaedia of Mathematics'', first Supplementary volume, 1988, , p. 281, articl"Halin Graph" and references therein. Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.. The cubic graph, cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Thomas Kirkman, Kirkman. Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prism Graph
In the mathematics, mathematical field of graph theory, a prism graph is a Graph (discrete mathematics), graph that has one of the prism (geometry), prisms as its skeleton. Examples The individual graphs may be named after the associated solid: * Triangular prism graph – 6 vertices, 9 edges * Cubical graph – 8 vertices, 12 edges * Pentagonal prism graph – 10 vertices, 15 edges * Hexagonal prism graph – 12 vertices, 18 edges * Heptagonal prism graph – 14 vertices, 21 edges * Octagonal prism graph – 16 vertices, 24 edges * ... Although geometrically the star polygons also form the faces of a different sequence of (self-intersecting and non-convex) prismatic polyhedra, the graphs of these star prisms are isomorphic to the prism graphs, and do not form a separate sequence of graphs. Construction Prism graphs are examples of generalized Petersen graphs, with parameters GP(''n'',1). They may also be constructed as the Cartesian product of graphs, Cartesian product of a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Altitude (triangle)
In geometry, an altitude of a triangle is a line segment through a given Vertex (geometry), vertex (called ''apex (geometry), apex'') and perpendicular to a line (geometry), line containing the side or edge (geometry), edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the ''base (geometry), base'' and ''extended side, extended base'' of the altitude. The point (geometry), point at the intersection of the extended base and the altitude is called the ''foot'' of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol , is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as ''dropping the altitude'' at that vertex. It is a special case of orthogonal projection. Altitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length (symbol ) equals the triangle's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Angle
In geometry, an angle of a polygon is formed by two adjacent edge (geometry), sides. For a simple polygon (non-self-intersecting), regardless of whether it is Polygon#Convexity and non-convexity, convex or non-convex, this angle is called an internal angle (or interior angle) if a point within the angle is in the interior of the polygon. A polygon has exactly one internal angle per vertex (geometry), vertex. If every internal angle of a simple polygon is less than a straight angle (pi, radians or 180°), then the polygon is called convex polygon, convex. In contrast, an external angle (also called a turning angle or exterior angle) is an angle formed by one side of a simple polygon and a Extended side, line extended from an adjacent side.Posamentier, Alfred S., and Lehmann, Ingmar. ''The Secrets of Triangles'', Prometheus Books, 2012. Properties * The sum of the internal angle and the external angle on the same vertex is radians (180°). * The sum of all the internal angl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Bipyramid
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid. Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century. Special cases As a right bipyramid Like other bipyramids, a triangular bipyramid can be constructed by attaching two tetrahedra face-to-face. These tetrahedra cover their triangular base, and the resulting polyhedron has six triangles, fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Polyhedron
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron. Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solids and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral polyhedron (one in which any two faces are equivalent .., and vice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |