|
Third Derivative
In calculus, a branch of mathematics, the third derivative or third-order derivative is the rate at which the second derivative, or the rate of change of the rate of change, is changing. The third derivative of a function y = f(x) can be denoted by :\frac,\quad f(x),\quad\text\frac (x) Other notations for differentiation can be used, but the above are the most common. Mathematical definitions Let f(x) = x^4. Then f'(x) = 4x^3 and f''(x) = 12x^2. Therefore, the third derivative of ''f'' is, in this case, : f(x) = 24x or, using Leibniz notation, : \frac ^4= 24x. Now for a more general definition. Let ''f'' be any function of ''x'' such that ''f'' ′′ is differentiable. Then the third derivative of ''f'' is given by : \frac (x)= \frac ''(x) The third derivative is the rate at which the second derivative (''f''′′(''x'')) is changing. Applications in geometry In differential geometry, the torsion of a curve — a fundamental property of curves in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations. Originally called infinitesimal calculus or "the calculus of infinitesimals", it has two major branches, differential calculus and integral calculus. The former concerns instantaneous Rate of change (mathematics), rates of change, and the slopes of curves, while the latter concerns accumulation of quantities, and areas under or between curves. These two branches are related to each other by the fundamental theorem of calculus. They make use of the fundamental notions of convergence (mathematics), convergence of infinite sequences and Series (mathematics), infinite series to a well-defined limit (mathematics), limit. It is the "mathematical backbone" for dealing with problems where variables change with time or another reference variable. Infinitesimal calculus was formulated separately ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kinematics
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics. Kinematics is concerned with systems of specification of objects' positions and velocities and mathematical transformations between such systems. These systems may be rectangular like Cartesian coordinate system, cartesian, Curvilinear coordinates like polar coordinates or other systems. The object trajectories may be specified with respect to other objects which may themselve be in motion relative to a standard reference. Rotating systems may also be used. Numerous practical problems in kinematics involve constraints, such as mechanical linkages, ropes, or rolling disks. Overview Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, Physical object, bodies (objects), and systems of bodies (group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Derivative (mathematics)
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. '' Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Aberrancy (geometry)
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus. Many specific curves have been thoroughly investigated using the synthetic approach. Differential geometry takes another path: curves are represented in a parametrized form, and their geometric properties and various quantities associated with them, such as the curvature and the arc length, are expressed via derivatives and integrals using vector calculus. One of the most important tools used to analyze a curve is the Frenet frame, a moving frame that provides a coordinate system at each point of the curve that is "best adapted" to the curve near that point. The theory of curves is much simpler and narrower in scope than the theory of surfaces and its higher-dimensional generalizations because a regular curve in a Euclidean space has no intrinsic geometry. Any regular curve may be parametrized by the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Decreasing Function
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory. In calculus and analysis In calculus, a function f defined on a subset of the real numbers with real values is called ''monotonic'' if it is either entirely non-decreasing, or entirely non-increasing. That is, as per Fig. 1, a function that increases monotonically does not exclusively have to increase, it simply must not decrease. A function is termed ''monotonically increasing'' (also ''increasing'' or ''non-decreasing'') if for all x and y such that x \leq y one has f\!\left(x\right) \leq f\!\left(y\right), so f preserves the order (see Figure 1). Likewise, a function is called ''monotonically decreasing'' (also ''decreasing'' or ''non-increasing'') if, whenever x \leq y, then f\!\left(x\right) \geq f\!\left(y\right), so i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inflation
In economics, inflation is an increase in the average price of goods and services in terms of money. This increase is measured using a price index, typically a consumer price index (CPI). When the general price level rises, each unit of currency buys fewer goods and services; consequently, inflation corresponds to a reduction in the purchasing power of money. The opposite of CPI inflation is deflation, a decrease in the general price level of goods and services. The common measure of inflation is the inflation rate, the annualized percentage change in a general price index. Changes in inflation are widely attributed to fluctuations in Real versus nominal value (economics), real demand for goods and services (also known as demand shocks, including changes in fiscal policy, fiscal or monetary policy), changes in available supplies such as during energy crisis, energy crises (also known as supply shocks), or changes in inflation expectations, which may be self-fulfilling. Moderat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nixon
Richard Milhous Nixon (January 9, 1913April 22, 1994) was the 37th president of the United States, serving from 1969 until his resignation in 1974. A member of the Republican Party, he previously served as the 36th vice president under President Dwight D. Eisenhower from 1953 to 1961, and also as a representative and senator from California. His presidency saw the reduction of U.S. involvement in the Vietnam War, '' détente'' with the Soviet Union and China, the Apollo 11 Moon landing, and the establishment of the Environmental Protection Agency and Occupational Safety and Health Administration. Nixon's second term ended early when he became the only U.S. president to resign from office, as a result of the Watergate scandal. Nixon was born into a poor family of Quakers in Yorba Linda, Southern California. He graduated from Whittier College with a Bachelor of Arts in 1934 and from Duke University with a Juris Doctor in 1937, practiced law in California, and then move ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector quantities (in that they have Magnitude (mathematics), magnitude and Direction (geometry), direction). The orientation of an object's acceleration is given by the orientation of the ''net'' force acting on that object. The magnitude of an object's acceleration, as described by Newton's second law, is the combined effect of two causes: * the net balance of all external forces acting onto that object — magnitude is Direct proportionality, directly proportional to this net resulting force; * that object's mass, depending on the materials out of which it is made — magnitude is Inverse proportionality, inversely proportional to the object's mass. The International System of Units, SI unit for acceleration is metre per second squared (, \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Position Function
In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents a point ''P'' in space. Its length represents the distance in relation to an arbitrary reference origin ''O'', and its direction represents the angular orientation with respect to given reference axes. Usually denoted x, r, or s, it corresponds to the straight line segment from ''O'' to ''P''. In other words, it is the displacement or translation that maps the origin to ''P'': :\mathbf=\overrightarrow. The term position vector is used mostly in the fields of differential geometry, mechanics and occasionally vector calculus. Frequently this is used in two-dimensional or three-dimensional space, but can be easily generalized to Euclidean spaces and affine spaces of any dimension.Keller, F. J., Gettys, W. E. et al. (1993), p. 28–29. Relative position The relative position of a point ''Q'' with respect to point ''P'' is the Euclidean vector resul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
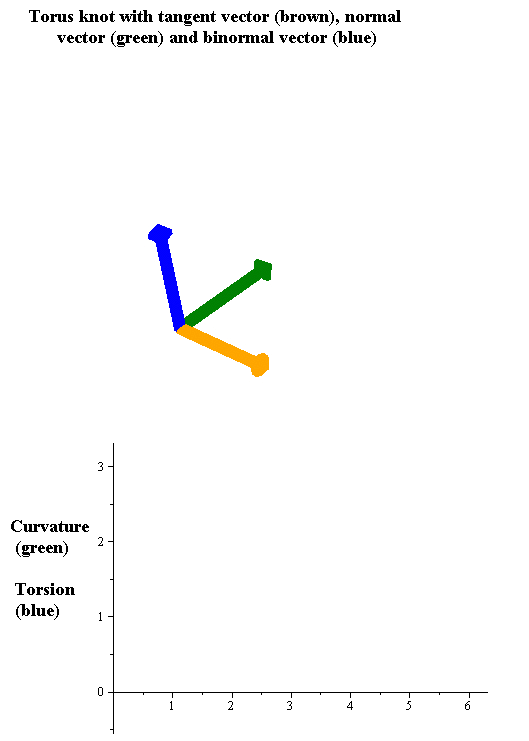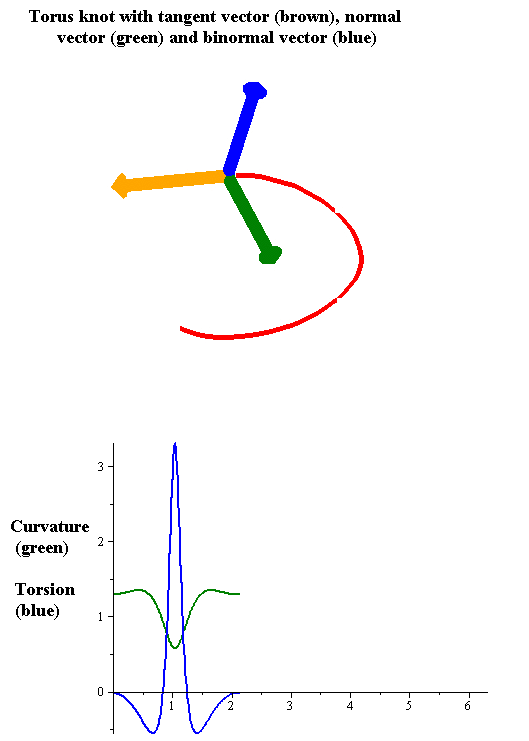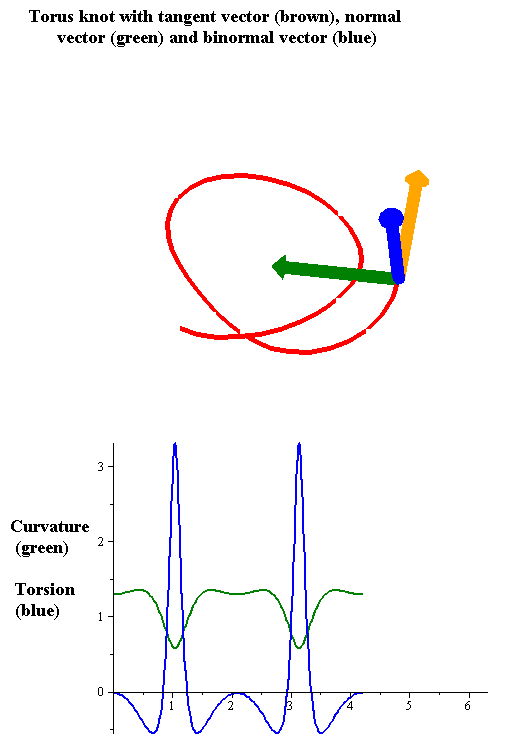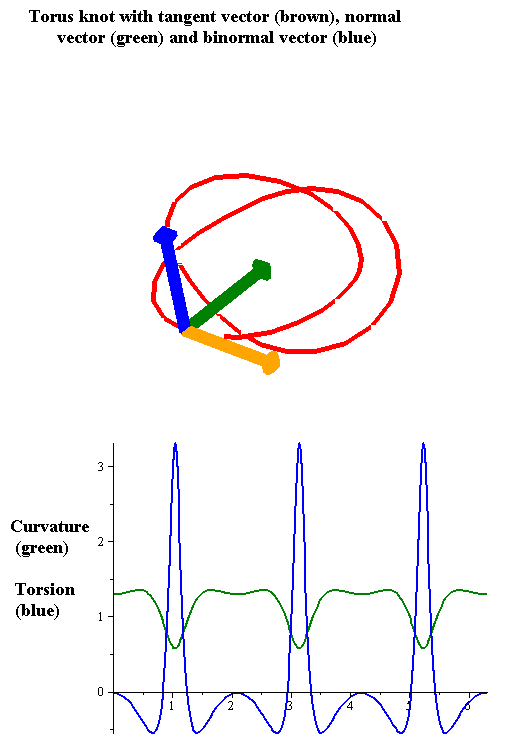
Torsion Of A Curve
In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas. Definition Let be a space curve parametrized by arc length and with the unit tangent vector . If the curvature of at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors : \mathbf=\frac, \quad \mathbf=\mathbf\times\mathbf respectively, where the prime denotes the derivative of the vector with respect to the parameter . The torsion measures the speed of rotation of the binormal vector at the given point. It is found from the equation : \mathbf' = -\tau\mathbf. which means : \tau = -\mathbf\cdot\math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |