|
Statistical Physics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science, information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscopic parameters that fluctuate about average values and are characterized by probability distributions. While classical thermodynamics is primarily concerned with thermodynamic equilibrium, statistical mechanics has been applied in non-equilibrium stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which relates to the order of nature, or, in other words, to the regular succession of events." It is one of the most fundamental scientific disciplines. "Physics is one of the most fundamental of the sciences. Scientists of all disciplines use the ideas of physics, including chemists who study the structure of molecules, paleontologists who try to reconstruct how dinosaurs walked, and climatologists who study how human activities affect the atmosphere and oceans. Physics is also the foundation of all engineering and technology. No engineer could design a flat-screen TV, an interplanetary spacecraft, or even a better mousetrap without first understanding the basic laws of physics. (...) You will come to see physics as a towering achievement of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluctuation–dissipation Theorem
The fluctuation–dissipation theorem (FDT) or fluctuation–dissipation relation (FDR) is a powerful tool in statistical physics for predicting the behavior of systems that obey detailed balance. Given that a system obeys detailed balance, the theorem is a proof that thermodynamic fluctuations in a physical variable predict the response quantified by the admittance or impedance (in their general sense, not only in electromagnetic terms) of the same physical variable (like voltage, temperature difference, etc.), and vice versa. The fluctuation–dissipation theorem applies both to classical and quantum mechanical systems. The fluctuation–dissipation theorem was proven by Herbert Callen and Theodore Welton in 1951 and expanded by Ryogo Kubo. There are antecedents to the general theorem, including Einstein's explanation of Brownian motion during his '' annus mirabilis'' and Harry Nyquist's explanation in 1928 of Johnson noise in electrical resistors. Qualitative overview a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics and chemistry, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Though there are many equations of state, none accurately predicts properties of substances under all conditions. The quest for a universal equation of state has spanned three centuries. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
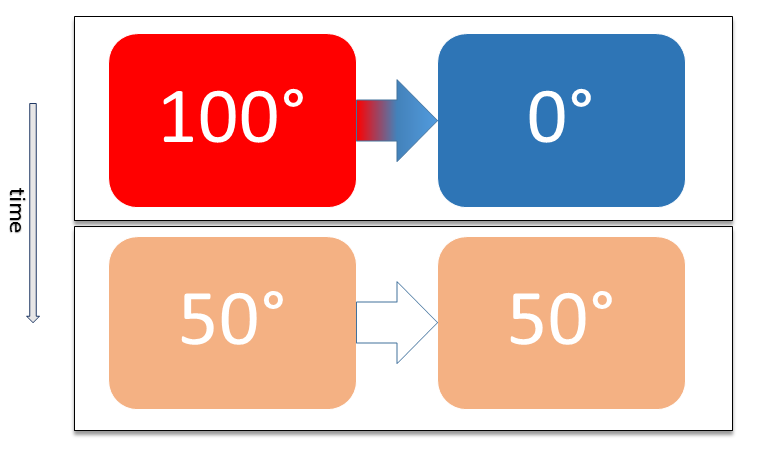
Thermal Equilibrium
Two physical systems are in thermal equilibrium if there is no net flow of thermal energy between them when they are connected by a path permeable to heat. Thermal equilibrium obeys the zeroth law of thermodynamics. A system is said to be in thermal equilibrium with itself if the temperature within the system is spatially uniform and temporally constant. Systems in thermodynamic equilibrium are always in thermal equilibrium, but the converse is not always true. If the connection between the systems allows transfer of energy as 'change in internal energy' but does not allow transfer of matter or transfer of energy as work, the two systems may reach thermal equilibrium without reaching thermodynamic equilibrium. Two varieties of thermal equilibrium Relation of thermal equilibrium between two thermally connected bodies The relation of thermal equilibrium is an instance of equilibrium between two bodies, which means that it refers to transfer through a selectively permeable par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transport Theory (statistical Physics)
Transport (in British English) or transportation (in American English) is the intentional Motion, movement of humans, animals, and cargo, goods from one location to another. Mode of transport, Modes of transport include aviation, air, land transport, land (rail transport, rail and road transport, road), ship transport, water, cable transport, cable, pipeline transport, pipelines, and space transport, space. The field can be divided into infrastructure, vehicles, and operations. Transport enables human trade, which is essential for the development of civilizations. Transport infrastructure consists of both fixed installations, including roads, railways, airway (aviation), airways, waterways, canals, and pipeline transport, pipelines, and terminals such as airports, train station, railway stations, bus stations, warehouses, trucking terminals, refueling depots (including fuel docks and fuel stations), and seaports. Terminals may be used both for the interchange of passengers and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
H-theorem
In classical statistical mechanics, the ''H''-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency of the quantity ''H'' (defined below) to decrease in a nearly-ideal gas of molecules.L. Boltzmann,Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen." Sitzungsberichte Akademie der Wissenschaften 66 (1872): 275-370. English translation: As this quantity ''H'' was meant to represent the entropy of thermodynamics, the ''H''-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions. The ''H''-theorem is a natural consequence of the kinetic equation derived by Boltzmann that has come to be known as Boltzmann's equation. The ''H''-theorem has led to considerable discuss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maxwell Distribution
Maxwell may refer to: People * Maxwell (surname), including a list of people and fictional characters with the name ** James Clerk Maxwell, mathematician and physicist * Justice Maxwell (other) * Maxwell baronets, in the Baronetage of Nova Scotia * Maxwell (footballer, born 1979), Brazilian forward * Maxwell (footballer, born 1981), Brazilian left-back * Maxwell (footballer, born 1986), Brazilian striker * Maxwell (footballer, born 1989), Brazilian left-back * Maxwell (footballer, born 1995), Brazilian forward * Maxwell (musician) (born 1973), American R&B and neo-soul singer * Maxwell (rapper) (born 1993), German rapper, member of rap band 187 Strassenbande * Maxwell Jacob Friedman (born 1996), American professional wrestler * Maxwell Silva (born 1953), Sri Lankan Sinhala Catholic cleric, Auxiliary Bishop of Colombo Places United States * Maxwell, California * Maxwell, Indiana * Maxwell, Iowa * Maxwell, Nebraska * Maxwell, New Mexico * Maxwell, Texas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rudolf Clausius
Rudolf Julius Emanuel Clausius (; 2 January 1822 – 24 August 1888) was a German physicist and mathematician and is considered one of the central founding fathers of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he gave the theory of heat a truer and sounder basis. His most important paper, "On the Moving Force of Heat", published in 1850, first stated the basic ideas of the second law of thermodynamics. In 1865 he introduced the concept of entropy. In 1870 he introduced the virial theorem, which applied to heat. Life Clausius was born in Köslin (now Koszalin, Poland) in the Province of Pomerania in Prussia. His father was a Protestant pastor and school inspector, and Rudolf studied in the school of his father. In 1838, he went to the Gymnasium in Stettin. Clausius graduated from the University of Berlin in 1844 where he had studied mathematics and physics since 1840 with, among others, Gustav Magnus, Peter Gusta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis. In 1863, Yale University awarded Gibbs the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism achieved the Unification (physics)#Unification of magnetism, electricity, light and related radiation, second great unification in physics, where Unification (physics)#Unification of gravity and astronomy, the first one had been realised by Isaac Newton. Maxwell was also key in the creation of statistical mechanics. With the publication of "A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric force, electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. (Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change and information systems including the transmission of information in telecommunication. Entropy is central to the second law of thermodynamics, which states that the entropy of an isolated system left to spontaneous evolution cannot decrease with time. As a result, isolated systems evolve toward thermodynamic equilibrium, where the entropy is highest. A consequence of the second law of thermodynamics is that certain processes are irreversible. The thermodynami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ludwig Boltzmann
Ludwig Eduard Boltzmann ( ; ; 20 February 1844 – 5 September 1906) was an Austrian mathematician and Theoretical physics, theoretical physicist. His greatest achievements were the development of statistical mechanics and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, S = k_ \ln \Omega, where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of the statistical disorder of a system. Max Planck named the constant the Boltzmann constant. Statistical mechanics is one of the pillars of modern physics. It describes how macroscopic observations (such as temperature and pressure) are related to microscopic parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity) to microscopic behavior, whereas, in classical thermodynamics, the only available option would be to measure and tabulate such quantities for various mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |