|
Stable Count Distribution
In probability theory, the stable count distribution is the conjugate prior of a Stable distribution#One-sided stable distribution and stable count distribution, one-sided stable distribution. This distribution was discovered by Stephen Lihn (Chinese: 藺鴻圖) in his 2017 study of daily distributions of the S&P 500 and the VIX. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy (mathematician), Paul Lévy, the first mathematician to have studied it. Of the three parameters defining the distribution, the stability parameter \alpha is most important. Stable count distributions have 0<\alpha<1. The known analytical case of is related to the VIX distribution (See Section 7 of ). All the moments are finite for the distribution. Definition Its standard distribution is defined as : |
Reliability Engineering
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability is defined as the probability that a product, system, or service will perform its intended function adequately for a specified period of time, OR will operate in a defined environment without failure. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The ''reliability function'' is theoretically defined as the probability of success. In practice, it is calculated using different techniques, and its value ranges between 0 and 1, where 0 indicates no probability of success while 1 indicates definite success. This probability is estimated from detailed (physics of failure) analysis, previous data sets, or through reliability testing and reliability modeling. Availability, testability, maintainability, and maintenance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rayleigh Distribution
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (). A Rayleigh distribution is often observed when the overall magnitude of a vector in the plane is related to its directional components. One example where the Rayleigh distribution naturally arises is when wind velocity is analyzed in two dimensions. Assuming that each component is uncorrelated, normally distributed with equal variance, and zero mean, which is infrequent, then the overall wind speed (vector magnitude) will be characterized by a Rayleigh distribution. A second example of the distribution arises in the case of random complex numbers whose real and imaginary components are independently and identically distributed Gaussian with equal variance and zero mean. In that case, the absolute v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Half-normal Distribution
In probability theory and statistics, the half-normal distribution is a special case of the folded normal distribution. Let X follow an ordinary normal distribution, N(0,\sigma^2). Then, Y=, X, follows a half-normal distribution. Thus, the half-normal distribution is a fold at the mean of an ordinary normal distribution with mean zero. Properties Using the \sigma parametrization of the normal distribution, the probability density function (PDF) of the half-normal is given by : f_Y(y; \sigma) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. Alternatively using a scaled precision (inverse of the variance) parametrization (to avoid issues if \sigma is near zero), obtained by setting \theta=\frac, the probability density function is given by : f_Y(y; \theta) = \frac\exp \left( -\frac \right) \quad y \geq 0, where E = \mu = \frac. The cumulative distribution function (CDF) is given by : F_Y(y; \sigma) = \int_0^y \frac\sqrt \, \exp \left( -\frac \rig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exponential Distribution
In probability theory and statistics, the exponential distribution or negative exponential distribution is the probability distribution of the distance between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate; the distance parameter could be any meaningful mono-dimensional measure of the process, such as time between production errors, or length along a roll of fabric in the weaving manufacturing process. It is a particular case of the gamma distribution. It is the continuous analogue of the geometric distribution, and it has the key property of being memoryless. In addition to being used for the analysis of Poisson point processes it is found in various other contexts. The exponential distribution is not the same as the class of exponential families of distributions. This is a large class of probability distributions that includes the exponential distribution as one of its members, but also includ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Shape Parameter
In probability theory and statistics, a shape parameter (also known as form parameter) is a kind of numerical parameter of a parametric family of probability distributionsEveritt B.S. (2002) Cambridge Dictionary of Statistics. 2nd Edition. CUP. that is neither a location parameter nor a scale parameter (nor a function of these, such as a rate parameter). Such a parameter must affect the ''shape (geometry), shape'' of a distribution rather than simply shifting it (as a location parameter does) or stretching/shrinking it (as a scale parameter does). For example, "peakedness" refers to how round the main peak is. Estimation Many estimators measure location or scale; however, estimators for shape parameters also exist. Most simply, they can be estimated in terms of the higher moment (mathematics), moments, using the Method of moments (statistics), method of moments, as in the ''skewness'' (3rd moment) or ''kurtosis'' (4th moment), if the higher moments are defined and finite. Estimato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generalized Gamma Distribution
The generalized gamma distribution is a continuous probability distribution with two shape parameters (and a scale parameter). It is a generalization of the gamma distribution which has one shape parameter (and a scale parameter). Since many distributions commonly used for parametric models in survival analysis (such as the exponential distribution, the Weibull distribution and the gamma distribution) are special cases of the generalized gamma, it is sometimes used to determine which parametric model is appropriate for a given set of data. Another example is the half-normal distribution. Characteristics The generalized gamma distribution has two shape parameters, d > 0 and p > 0, and a scale parameter, a > 0. For non-negative ''x'' from a generalized gamma distribution, the probability density function is : f(x; a, d, p) = \frac, where \Gamma(\cdot) denotes the gamma function. The cumulative distribution function is : F(x; a, d, p) = \frac , \text \, P\left( \frac, \left( \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chi Distribution
In probability theory and statistics, the chi distribution is a continuous probability distribution over the non-negative real line. It is the distribution of the positive square root of a sum of squared independent Gaussian random variables. Equivalently, it is the distribution of the Euclidean distance between a multivariate Gaussian random variable and the origin. The chi distribution describes the positive square roots of a variable obeying a chi-squared distribution. If Z_1, \ldots, Z_k are k independent, normally distributed random variables with mean 0 and standard deviation 1, then the statistic :Y = \sqrt is distributed according to the chi distribution. The chi distribution has one positive integer parameter k, which specifies the degrees of freedom (i.e. the number of random variables Z_i). The most familiar examples are the Rayleigh distribution (chi distribution with two degrees of freedom) and the Maxwell–Boltzmann distribution of the molecular speeds i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
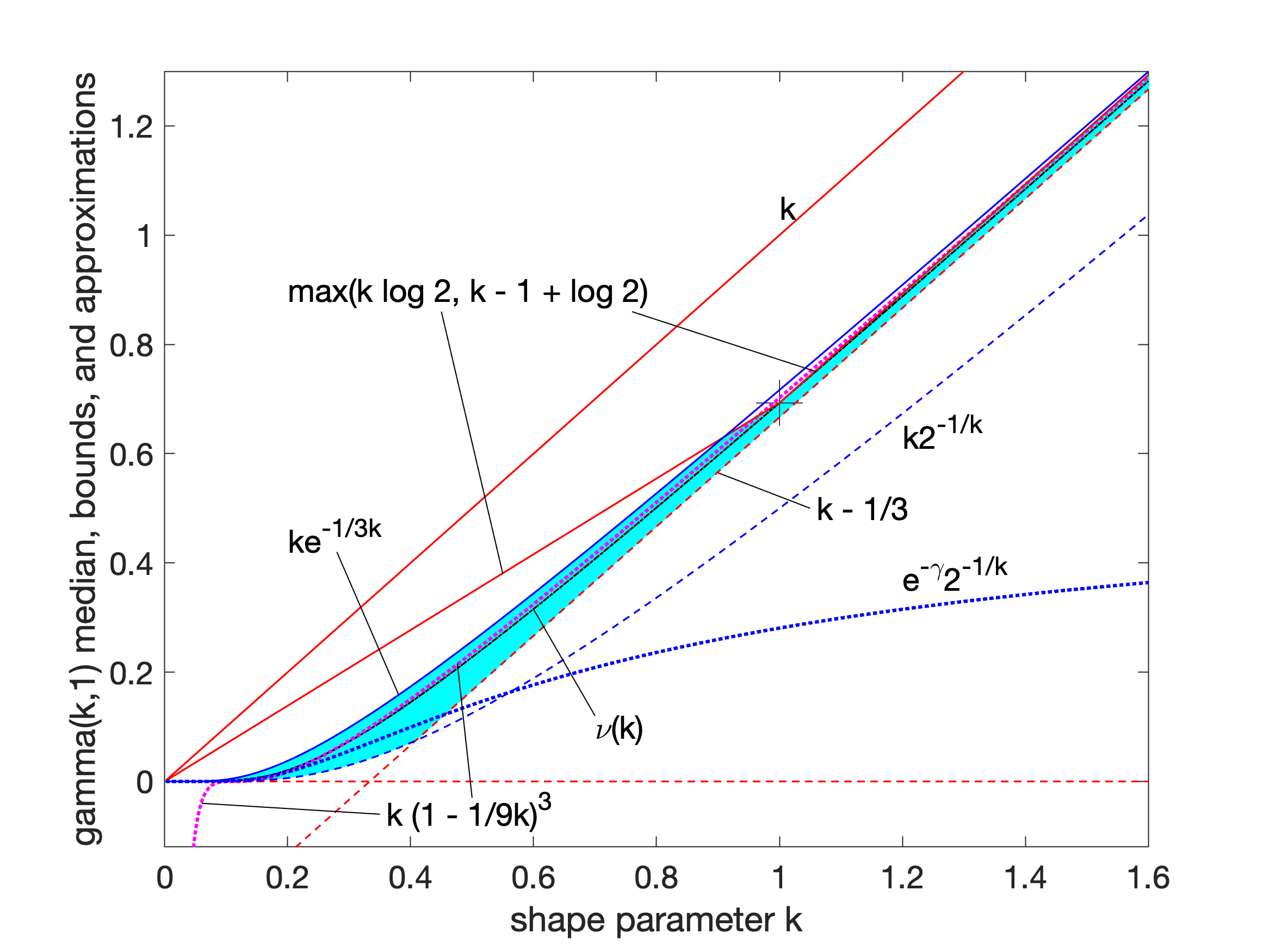
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chi-squared Distribution
In probability theory and statistics, the \chi^2-distribution with k Degrees of freedom (statistics), degrees of freedom is the distribution of a sum of the squares of k Independence (probability theory), independent standard normal random variables. The chi-squared distribution \chi^2_k is a special case of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim \chi^2_k then X \sim \text(\alpha=\frac, \theta=2) (where \alpha is the shape parameter and \theta the scale parameter of the gamma distribution) and X \sim \text_1(1,k) . The scaled chi-squared distribution s^2 \chi^2_k is a reparametrization of the gamma distribution and the univariate Wishart distribution. Specifically if X \sim s^2 \chi^2_k then X \sim \text(\alpha=\frac, \theta=2 s^2) and X \sim \text_1(s^2,k) . The chi-squared distribution is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in constru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution () is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event. It can also be used for the number of events in other types of intervals than time, and in dimension greater than 1 (e.g., number of events in a given area or volume). The Poisson distribution is named after French mathematician Siméon Denis Poisson. It plays an important role for discrete-stable distributions. Under a Poisson distribution with the expectation of ''λ'' events in a given interval, the probability of ''k'' events in the same interval is: :\frac . For instance, consider a call center which receives an average of ''λ ='' 3 calls per minute at all times of day. If the calls are independent, receiving one does not change the probability of when the next on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |