|
Squaring The Circle
Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square (geometry), square with the area of a circle, area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of Line (geometry), lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the zero of a function, root of any polynomial with Rational number, rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compass And Straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an Idealization (science philosophy), idealized ruler and a Compass (drawing tool), compass. The idealized ruler, known as a straightedge, is assumed to be infinite in length, have only one edge, and no markings on it. The compass is assumed to have no maximum or minimum radius, and is assumed to "collapse" when lifted from the page, so it may not be directly used to transfer distances. (This is an unimportant restriction since, using a multi-step procedure, a distance can be transferred even with a collapsing compass; see compass equivalence theorem. Note however that whilst a non-collapsing compass held against a straightedge might seem to be equivalent to marking it, the neusis construction is still impermissible and this is what unmarked really ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
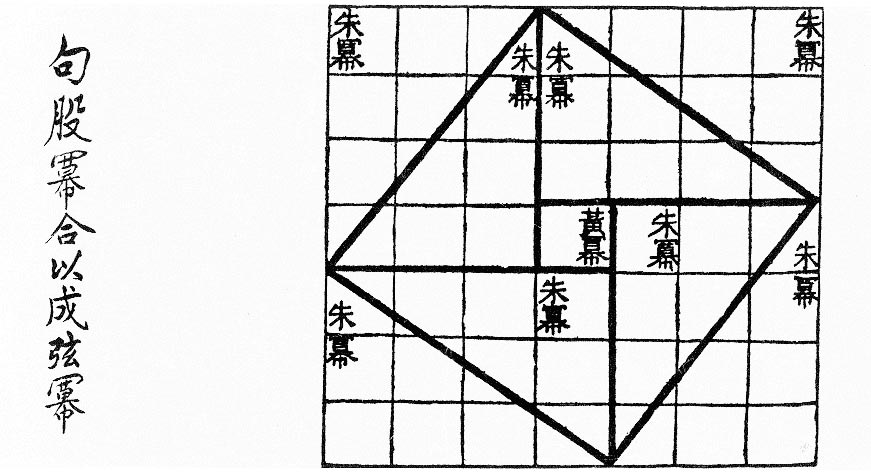
Squaring The Circle J
Squaring may refer to: *Square (algebra), the result of multiplying something by itself *Quadrature (geometry), Quadrature (mathematics), the process of determining the area of a plane figure {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximations Of π
Approximation#Mathematics, Approximations for the mathematical constant pi () in the history of mathematics reached an accuracy within 0.04% of the true value before the beginning of the Common Era. In Chinese mathematics, this was improved to approximations correct to what corresponds to about seven decimal digits by the 5th century. Further progress was not made until the 14th century, when Madhava of Sangamagrama developed approximations correct to eleven and then thirteen digits. Jamshīd al-Kāshī achieved sixteen digits next. Early modern mathematicians reached an accuracy of 35 digits by the beginning of the 17th century (Ludolph van Ceulen), and 126 digits by the 19th century (Jurij Vega). The record of manual approximation of is held by William Shanks, who calculated 527 decimals correctly in 1853. Since the middle of the 20th century, the approximation of has been the task of electronic digital computers (for a comprehensive account, see chronology of computation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Milü
''Milü'' (), also known as Zulü (Zu's ratio), is the name given to an approximation of ( pi) found by the Chinese mathematician and astronomer Zu Chongzhi during the 5th century. Using Liu Hui's algorithm, which is based on the areas of regular polygons approximating a circle, Zu computed as being between 3.1415926 and 3.1415927 and gave two rational approximations of , and , which were named ''yuelü'' () and ''milü'' respectively. is the best rational approximation of with a denominator of four digits or fewer, being accurate to six decimal places. It is within % of the value of , or in terms of common fractions overestimates by less than . The next rational number (ordered by size of denominator) that is a better rational approximation of is , though it is still only correct to six decimal places. To be accurate to seven decimal places, one needs to go as far as . For eight, is needed. The accuracy of ''milü'' to the true value of can be explained using the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zu Chongzhi
Zu Chongzhi (; 429 – 500), courtesy name Wenyuan (), was a Chinese astronomer, inventor, mathematician, politician, and writer during the Liu Song and Southern Qi dynasties. He was most notable for calculating pi as between 3.1415926 and 3.1415927, a record in precision which would not be surpassed for nearly 900 years. Life and works Chongzhi's ancestry was from modern Baoding, Hebei. To flee from the ravages of war, Zu's grandfather Zu Chang moved to the Yangtze, as part of the massive population movement during the Eastern Jin. Zu Chang () at one point held the position of Chief Minister for the Palace Buildings () within the Liu Song and was in charge of government construction projects. Zu's father, Zu Shuozhi (), also served the court and was greatly respected for his erudition. Zu was born in Jiankang. His family had historically been involved in astronomical research, and from childhood Zu was exposed to both astronomy and mathematics. When he was only a youth, his t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu ( The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state of Cao Wei during the Three Kingdoms period (220–280 CE) of China. His major contributions as recorded in his commentary on ''The Nine Chapters on the Mathematical Art'' include a proof of the Pythagorean theorem, theorems in solid geometry, an improvement on Archimedes's approximation of , and a systematic method of solving linear equations in several unknowns. In his other work, '' Haidao Suanjing (The Sea Island Mathematical Manual)'', he wrote about geometrical problems and their application to surveying. He probably visited Luoyang, where he measured the sun's shadow. Mathematical work Liu Hui expressed mathematical results in the form of decimal fractions that utilized metrological units (i.e., related units of length wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chinese Mathematics
Mathematics emerged independently in China by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system (base 2, binary and base 10, decimal), algebra, geometry, number theory and trigonometry. Since the Han dynasty, as diophantine approximation being a prominent numerical method, the Chinese made substantial progress on polynomial evaluation. Algorithms like regula falsi and expressions like simple continued fractions are widely used and have been well-documented ever since. They deliberately find the principal nth root, ''n''th root of positive numbers and the zero of a function, roots of equations. The major texts from the period, ''The Nine Chapters on the Mathematical Art'' and the ''Book on Numbers and Computation'' gave detailed processes for solving various mathematical problems in daily life. All procedures were computed using a counting board in both texts, and they ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shulba Sutras
The ''Shulva Sutras'' or ''Śulbasūtras'' (Sanskrit: शुल्बसूत्र; ': "string, cord, rope") are sutra texts belonging to the Śrauta ritual and containing geometry related to vedi (altar), fire-altar construction. Purpose and origins The Shulba Sutras are part of the larger corpus of texts called the Kalpa (Vedanga), Shrauta Sutras, considered to be appendices to the Vedas. They are the only sources of knowledge of Indian mathematics from the Vedic period. Unique Vedi (altar), Vedi (fire-altar) shapes were associated with unique gifts from the Gods. For instance, "he who desires heaven is to construct a fire-altar in the form of a falcon"; "a fire-altar in the form of a tortoise is to be constructed by one desiring to win the world of Brahman" and "those who wish to destroy existing and future enemies should construct a fire-altar in the form of a rhombus"., p. 387, "Certain shapes and sizes of fire-altars were associated with particular gifts that the sacrif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shatapatha Brahmana
The Shatapatha Brahmana (, , abbreviated to 'SB') is a commentary on the Yajurveda, Śukla Yajurveda. It is attributed to the Vedic sage Yajnavalkya. Described as the most complete, systematic, and important of the Brahmanas (commentaries on the Vedas), it contains detailed explanations of Historical Vedic religion, Vedic Yajna, sacrificial rituals, symbolism, and mythology. Particularly in its description of sacrificial rituals (including construction of complex fire-altars). The Shatapatha Brahmana is also considered significant in the development of Vaishnavism as the origin of several Puranas, Puranic legends and avatars of Vishnu. Notably, all of them (Matsya, Kurma, Varaha, Narasimha, and Vamana) are listed as the first five avatars in the Dashavatara (the ten principal avatars of Vishnu). There are two versions (recensions) available of this text. They are the Madhyandina Shakha, Madhyandina recension and the Kanva Shakha, Kanva recension. This article focuses exclusively ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indian Mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, Bhaskara II, Varāhamihira, and Madhava of Sangamagrama, Madhava. The Decimal, decimal number system in use today: "The measure of the genius of Indian civilisation, to which we owe our modern (number) system, is all the greater in that it was the only one in all history to have achieved this triumph. Some cultures succeeded, earlier than the Indian, in discovering one or at best two of the characteristics of this intellectual feat. But none of them managed to bring together into a complete and coherent system the necessary and sufficient conditions for a number-system with the same potential as our own." was first recorded in Indian mathematics. Indian mathematicians made early contributions to the study of the concept of 0 (number), ze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |