|
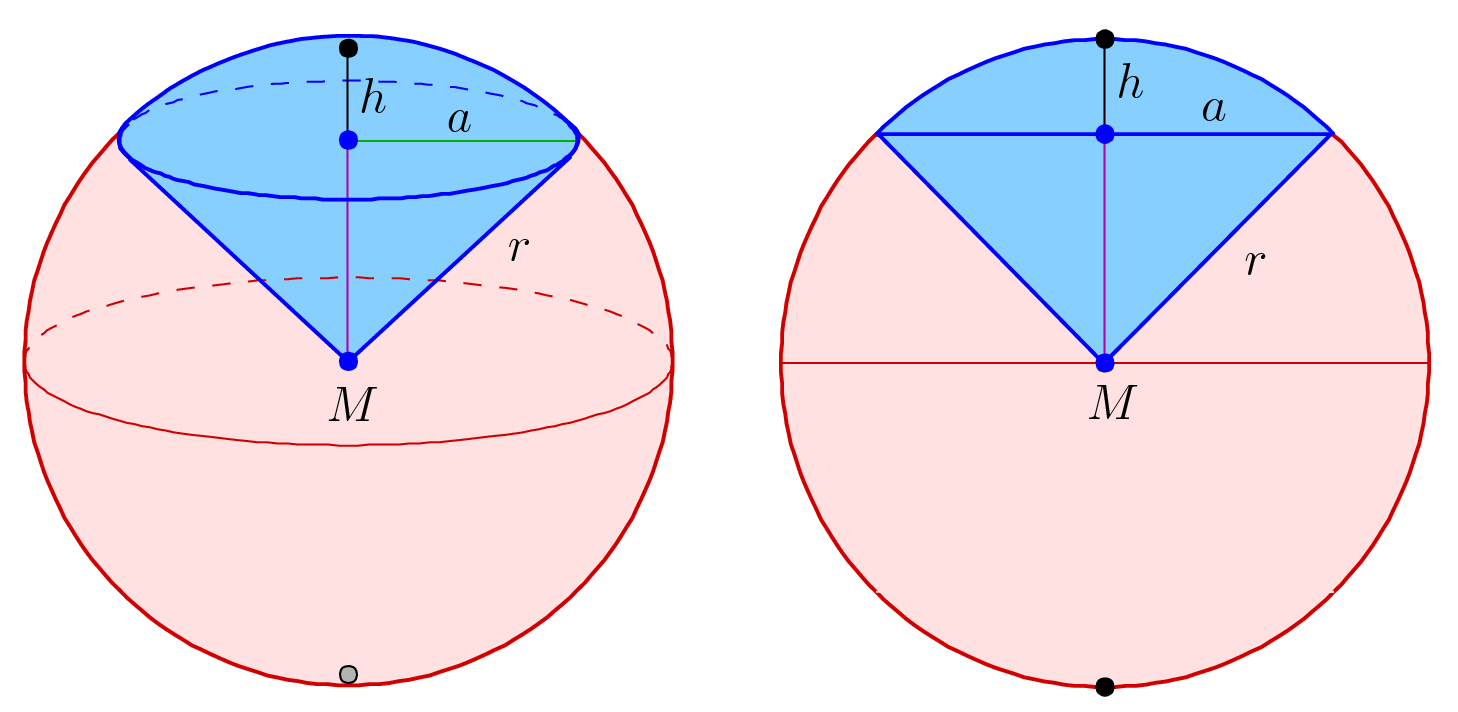
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is V = \frac\,. This may also be written as V = \frac (1-\cos\varphi)\,, where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere. The height, is given by h = r (1-\cos\varphi)\,. The volume of the sector is related to the area of the cap by: V = \frac\,. Area The curved surface area of the spherical se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Segment
In geometry, a spherical segment is the solid defined by cutting a sphere or a ball with a pair of parallel planes. It can be thought of as a spherical cap with the top truncated, and so it corresponds to a spherical frustum. The surface of the ''spherical segment'' (excluding the bases) is called spherical zone. If the radius of the sphere is called , the radii of the spherical segment bases are and , and the height of the segment (the distance from one parallel plane to the other) called , then the volume of the spherical segment is : V = \frac h \left(3 a^2 + 3 b^2 + h^2\right). For the special case of the top plane being tangent to the sphere, we have b = 0 and the solid reduces to a spherical cap. The equation above for volume of the spherical segment can be arranged to : V = \biggl \pi a^2 \left (\frac \biggr ) \right + \biggl \pi b^2 \left ( \frac \biggr ) \right + \biggl \frac \pi \left( \frac \right)^3 \biggr /math> Thus, the segment volume equals the su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Cap
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball (mathematics), ball cut off by a plane (mathematics), plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center (geometry), center of the sphere (forming a great circle), so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a ''Sphere#Hemisphere, hemisphere''. Volume and surface area The volume of the spherical cap and the area of the curved surface may be calculated using combinations of * The radius r of the sphere * The radius a of the base of the cap * The height h of the cap * The Spherical coordinate system, polar angle \theta between the rays from the center of the sphere to the apex of the cap (the pole) and the edge of the disk (mathematics), disk forming the base of the cap. These variables are inter-related through the formulas a = r \sin \theta, h = r ( 1 - \cos \theta ), 2hr = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Volume Element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form \mathrmV = \rho(u_1,u_2,u_3)\,\mathrmu_1\,\mathrmu_2\,\mathrmu_3 where the u_i are the coordinates, so that the volume of any set B can be computed by \operatorname(B) = \int_B \rho(u_1,u_2,u_3)\,\mathrmu_1\,\mathrmu_2\,\mathrmu_3. For example, in spherical coordinates \mathrmV = u_1^2\sin u_2\,\mathrmu_1\,\mathrmu_2\,\mathrmu_3, and so \rho = u_1^2\sin u_2. The notion of a volume element is not limited to three dimensions: in two dimensions it is often known as the area element, and in this setting it is useful for doing surface integrals. Under changes of coordinates, the volume element changes by the absolute value of the Jacobian determinant of the coordinate transformation (by the change of variables formula). This fact allows volume el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steradian
The steradian (symbol: sr) or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. A solid angle in the form of a circular cone can be projected onto a sphere from its centre, delineating a spherical cap where the cone intersects the sphere. The magnitude of the solid angle expressed in steradians is defined as the quotient of the surface area of the spherical cap and the square of the sphere's radius. This is analogous to the way a plane angle projected onto a circle delineates a circular arc on the circumference, whose length is proportional to the angle. Steradians can be used to measure a solid angle of any projected shape. The solid angle subtended is the same as that of a cone with the same projected area. A solid angle of one steradian subtends a cone aperture of approximately 1.144 radians or 65.54 degrees. In the SI, solid angle i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Angle
In geometry, a solid angle (symbol: ) is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the ''apex'' of the solid angle, and the object is said to '' subtend'' its solid angle at that point. In the International System of Units (SI), a solid angle is expressed in a dimensionless unit called a ''steradian'' (symbol: sr), which is equal to one square radian, sr = rad2. One steradian corresponds to one unit of area (of any shape) on the unit sphere surrounding the apex, so an object that blocks all rays from the apex would cover a number of steradians equal to the total surface area of the unit sphere, 4\pi. Solid angles can also be measured in squares of angular measures such as degrees, minutes, and seconds. A small object nearby may subtend the same solid angle as a larger object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
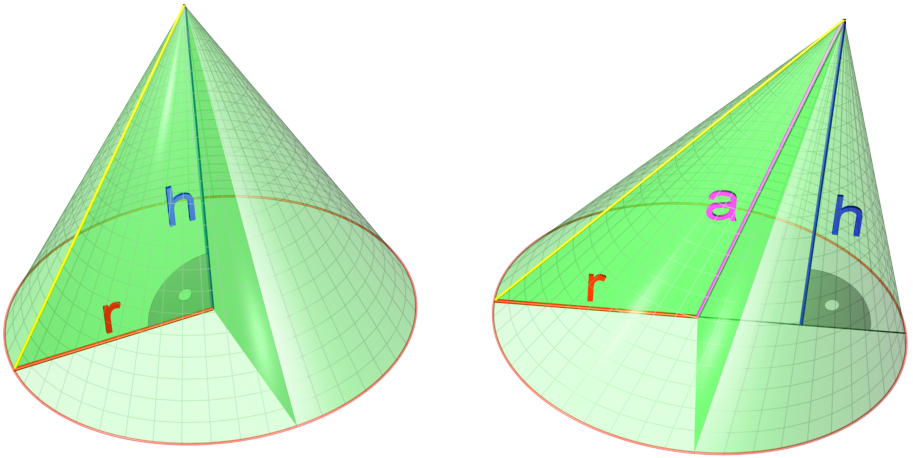
Cone Aperture
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the ''apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Sector
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle. Volume If the radius of the sphere is denoted by and the height of the cap by , the volume of the spherical sector is V = \frac\,. This may also be written as V = \frac (1-\cos\varphi)\,, where is half the cone aperture angle, i.e., is the angle between the rim of the cap and the axis direction to the middle of the cap as seen from the sphere center. The limiting case is for approaching 180 degrees, which then describes a complete sphere. The height, is given by h = r (1-\cos\varphi)\,. The volume of the sector is related to the area of the cap by: V = \frac\,. Area The curved surface area of the spherical se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Sector
A circular sector, also known as circle sector or disk sector or simply a sector (symbol: ⌔), is the portion of a disk (a closed region bounded by a circle) enclosed by two radii and an arc, with the smaller area being known as the ''minor sector'' and the larger being the ''major sector''. In the diagram, is the central angle, the radius of the circle, and is the arc length of the minor sector. The angle formed by connecting the endpoints of the arc to any point on the circumference that is not in the sector is equal to half the central angle. Types A sector with the central angle of 180° is called a '' half-disk'' and is bounded by a diameter and a semicircle. Sectors with other central angles are sometimes given special names, such as quadrants (90°), sextants (60°), and octants (45°), which come from the sector being one quarter, sixth or eighth part of a full circle, respectively. Area The total area of a circle is . The area of the sector can be obtai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |