|
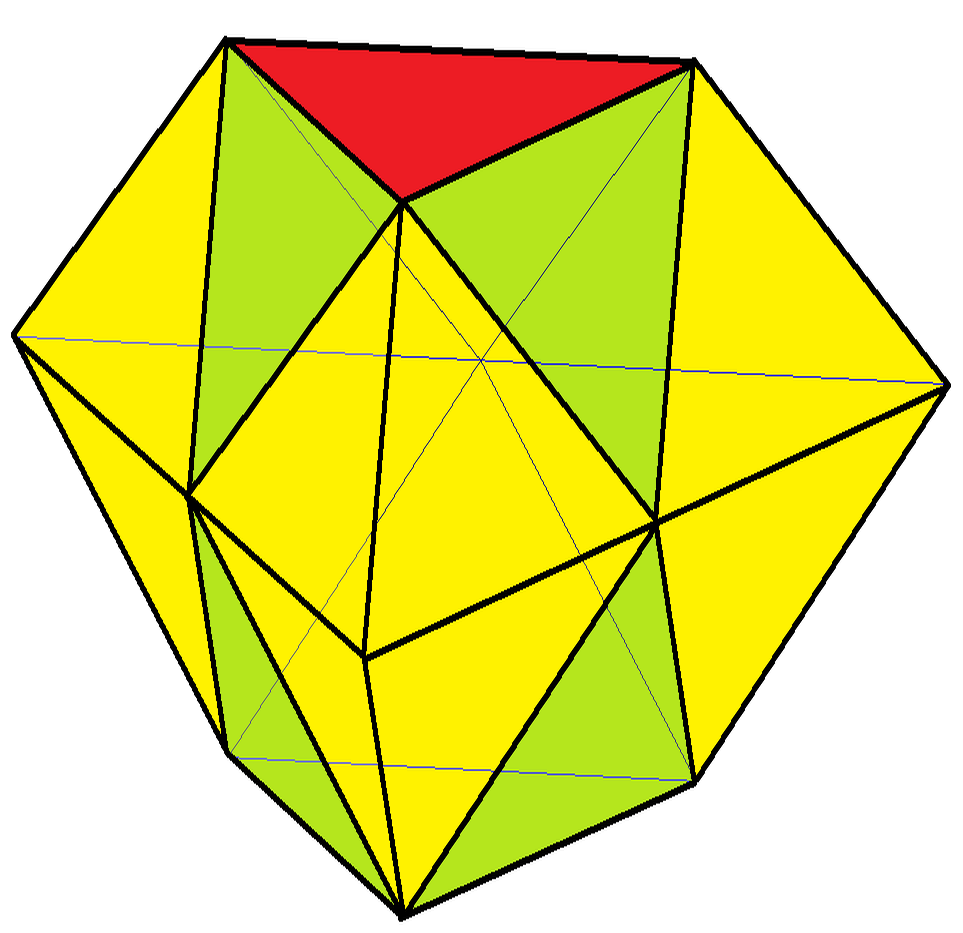
Spherical Octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of irregular octahedra also exist, including both convex and non-convex shapes. Combinatorially equivalent to the regular octahedron The following polyhedra are combinatorially equivalent to the regular octahedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of it: * Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles. The regular octahedron is a special case in which the six lateral triangles are also equilateral. * Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyrobifastigium
In geometry, the gyrobifastigium is a polyhedron that is constructed by attaching a triangular prism to square face of another one. It is an example of a Johnson solid. It is the only Johnson solid that can tile three-dimensional space. Construction and its naming The gyrobifastigium can be constructed by attaching two triangular prisms along corresponding square faces, giving a quarter-turn to one prism. These prisms cover the square faces so the resulting polyhedron has four equilateral triangles and four squares, making eight faces in total, an octahedron. Because its faces are all regular polygons and it is convex, the gyrobifastigium is a Johnson solid, indexed as J_ . The name of the gyrobifastigium comes from the Latin ''fastigium'', meaning a sloping roof. In the standard naming convention of the Johnson solids, ''bi-'' means two solids connected at their bases, and ''gyro-'' means the two halves are twisted with respect to each other. Cartesian coordinates for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elongated Triangular Bipyramid
In geometry, the elongated triangular bipyramid (or dipyramid) or triakis triangular prism a polyhedron constructed from a triangular prism by attaching two tetrahedrons to its bases. It is an example of Johnson solid. Construction The elongated triangular bipyramid is constructed from a triangular prism by attaching two tetrahedrons onto its bases, a process known as the elongation. These tetrahedrons cover the triangular faces so that the resulting polyhedron has nine faces (six of them are equilateral triangles and three of them are squares), fifteen edges, and eight vertices. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid. The elongated bipyramid is one of them, enumerated as the fourteenth Johnson solid J_ . Properties The surface area of an elongated triangular bipyramid A is the sum of all polygonal face's area: six equilateral triangles and three squares. The volume of an elongated triangular bipyramid V can be ascertaine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Bifrustum
In geometry, the triangular bifrustum is the second in an infinite series of bifrustum polyhedra. It has 6 trapezoid and 2 triangle faces. It may also be called the truncated triangular bipyramid; however, that term is ambiguous, as it may also refer to polyhedra formed by Truncation (geometry), truncating all five vertices of a triangular bipyramid. This polyhedron can be constructed by taking a triangular bipyramid and truncating the polar axis vertices, making it into two end-to-end frustums. It appears as the form of certain nanocrystals.. A truncated triangular bipyramid can be constructed by connecting two stacked regular octahedra with 3 pairs of tetrahedra around the sides. This represents a portion of the gyrated alternated cubic honeycomb. : References {{reflist External linksConway Notation for Polyhedra Try: t3dP3 Polyhedra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kite (geometry)
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word ''deltoid'' may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals.See H. S. M. Coxeter's review of in : "It is unfortunate that the author uses, instead of 'kite', the name 'deltoid', which belongs more properly to a curve, the three-cusped hypocycloid." A kite may also be called a dart, particularly if it is not convex. Every kite is an orthodiagonal quadrilateral (its diagonals are at right angles) and, when convex, a tangential quadrilateral (its sides are tangent to an inscribed circle). The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites, with two opposite right angles; the rhombus, rhombi, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetragonal Trapezohedron
In geometry, a tetragonal trapezohedron, or deltohedron, is the second in an infinite series of trapezohedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism. Applications In mesh generation This shape has been used as a test case for hexahedral mesh generation,..... simplifying an earlier test case posited by mathematician Robert Schneiders in the form of a square pyramid with its boundary subdivided into 16 quadrilaterals. In this context the tetragonal trapezohedron has also been called the cubical octahedron, quadrilateral octahedron, or octagonal spindle, because it has eight quadrilateral faces and is uniquely defined as a combinatorial polyhedron by that property. Adding four cuboids to a mesh for the cubical octahedron would also give a mesh for Schneiders' pyramid. As a simply-connected polyhedron with an even number of quadrilateral faces, the cubical octahedron can be decomposed into topologica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isosceles Triangle
In geometry, an isosceles triangle () is a triangle that has two Edge (geometry), sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the Golden triangle (mathematics), golden triangle, and the faces of bipyramids and certain Catalan solids. The mathematical study of isosceles triangles dates back to ancient Egyptian mathematics and Babylonian mathematics. Isosceles triangles have been used as decoration from even earlier times, and appear frequently in architecture and design, for instance in the pediments and gables of buildings. The two equal sides are called the ''legs'' and the third side is called the base (geometry), ''base'' of the triangle. The other dimensions of the triangle, such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heptagon
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon. The heptagon is sometimes referred to as the septagon, using ''Wikt:septa-, septa-'' (an elision of ''Wikt:septua-, septua-''), a Latin-derived numerical prefix, rather than ''Wikt:hepta-, hepta-'', a Greek language, Greek-derived numerical prefix (both are cognate), together with the suffix ''-gon'' for , meaning angle. Regular heptagon A regular polygon, regular heptagon, in which all sides and all angles are equal, has internal angles of 5π/7 radians (128 degree (angle), degrees). Its Schläfli symbol is . Area The area (''A'') of a regular heptagon of side length ''a'' is given by: :A = \fraca^2 \cot \frac \simeq 3.634 a^2. This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with Vertex (geometry), vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half the cotangent of \pi/7 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex (geometry), apex. Each base edge (geometry), edge and apex form a triangle, called a lateral face. A pyramid is a cone, conic solid with a polygonal base. Many types of pyramids can be found by determining the shape of bases, either by based on a regular polygon (regular pyramids) or by cutting off the apex (truncated pyramid). It can be generalized into higher dimensions, known as hyperpyramid. All pyramids are Self-dual polyhedron, self-dual. Etymology The word "pyramid" derives from the ancient Greek term "πυραμίς" (pyramis), which referred to a pyramid-shaped structure and a type of wheat cake. The term is rooted in the Greek "πυρ" (pyr, 'fire') and "άμις" (amis, 'vessel'), highlighting the shape's pointed, flame-like appearance. In Byzantine Greek, the term evolved to "πυραμίδα" (pyramída), continuing to denote pyramid structures. The Greek term " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangular Cupola
In geometry, the triangular cupola is the cupola with hexagon as its base and triangle as its top. If the edges are equal in length, the triangular cupola is the Johnson solid. It can be seen as half a cuboctahedron. The triangular cupola can be applied to construct many polyhedrons. Properties The triangular cupola has 4 triangles, 3 squares, and 1 hexagon as their faces; the hexagon is the base and one of the four triangles is the top. If all of the edges are equal in length, the triangles and the hexagon becomes regular. The dihedral angle between each triangle and the hexagon is approximately 70.5°, that between each square and the hexagon is 54.7°, and that between square and triangle is 125.3°. A convex polyhedron in which all of the faces are regular is a Johnson solid, and the triangular cupola is among them, enumerated as the third Johnson solid J_ . Given that a is the edge length of a triangular cupola. Its surface area A can be calculated by adding t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Pyramid
In geometry, a square pyramid is a Pyramid (geometry), pyramid with a square base and four triangles, having a total of five faces. If the Apex (geometry), apex of the pyramid is directly above the center of the square, it is a ''right square pyramid'' with four isosceles triangles; otherwise, it is an ''oblique square pyramid''. When all of the pyramid's edges are equal in length, its triangles are all equilateral triangle, equilateral. It is called an ''equilateral square pyramid'', an example of a Johnson solid. Square pyramids have appeared throughout the history of architecture, with examples being Egyptian pyramids and many other similar buildings. They also occur in chemistry in Square pyramidal molecular geometry, square pyramidal molecular structures. Square pyramids are often used in the construction of other polyhedra. Many mathematicians in ancient times discovered the formula for the volume of a square pyramid with different approaches. Special cases Right squar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augmented Triangular Prism
In geometry, the augmented triangular prism is a polyhedron constructed by attaching an equilateral square pyramid onto the square face of a triangular prism. As a result, it is an example of Johnson solid. It can be visualized as the chemical compound, known as capped trigonal prismatic molecular geometry. Construction The augmented triangular prism can be constructed from a triangular prism by attaching an equilateral square pyramid to one of its square faces, a process known as augmentation. This square pyramid covers the square face of the prism, so the resulting polyhedron has 6 equilateral triangles and 2 squares as its faces. A convex polyhedron in which all faces are regular is Johnson solid, and the augmented triangular prism is among them, enumerated as 49th Johnson solid J_ . Properties An augmented triangular prism with edge length a has a surface area, calculated by adding six equilateral triangles and two squares' area: \fraca^2 \approx 4.598a^2. Its v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |