|
Shell Integration
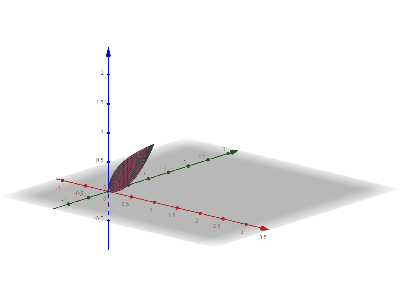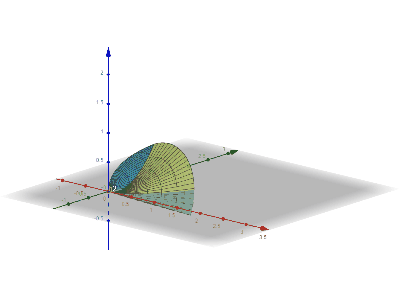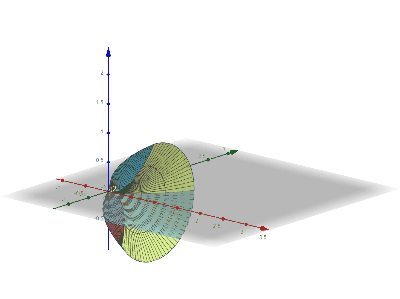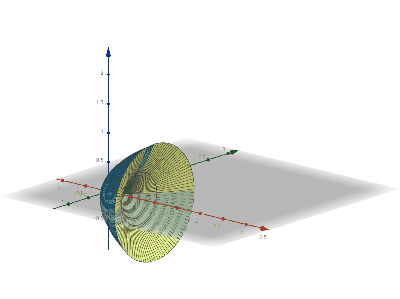
Shell integration (the shell method in integral calculus) is a method for calculating the volume of a solid of revolution, when integrating along an axis ''perpendicular to'' the axis of revolution. This is in contrast to disc integration which integrates along the axis ''parallel'' to the axis of revolution. Definition The shell method goes as follows: Consider a volume in three dimensions obtained by rotating a cross-section in the -plane around the -axis. Suppose the cross-section is defined by the graph of the positive function on the interval . Then the formula for the volume will be: :2 \pi \int_a^b x f(x)\, dx If the function is of the coordinate and the axis of rotation is the -axis then the formula becomes: :2 \pi \int_a^b y f(y)\, dy If the function is rotating around the line then the formula becomes: :\begin \displaystyle 2 \pi \int_a^b (x-h) f(x)\,dx, & \text\ h \le a < b\\ \displaystyle 2 \pi \int_a^b (h-x) f(x)\,dx, & \text\ a < b \le h, \end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Shell Integral Undergraph - Around Y-axis
Shell may refer to: Architecture and design * Shell (structure), a thin structure ** Concrete shell, a thin shell of concrete, usually with no interior columns or exterior buttresses Science Biology * Seashell, a hard outer layer of a marine animal, found on beaches * Eggshell * Nutshell * Exoskeleton, an external covering of some animals ** Mollusc shell *** Bivalve shell *** Gastropod shell ** Shell, of a brachiopod * Turtle shell * Armadillo shell Physics and chemistry * Electron shell or a principal energy level of electrons outside an atom's nucleus * Nuclear shell model, a principal energy level of nucleons within an atom's nucleus * On shell and off shell, quantum field theory concepts depending on whether classical equations of motion are obeyed Mathematics * Spherical shell Organisations * Shell plc formerly Royal Dutch Shell plc, a British multinational oil and gas company ** Shell Oil Company or Shell USA ** Shell Australia ** Shell Canada ** Shell Nigeria * Shell co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Integral Calculus
In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter. A definite integral computes the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an ''antiderivative'', a function whose der ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calculation
A calculation is a deliberate mathematical process that transforms a plurality of inputs into a singular or plurality of outputs, known also as a result or results. The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm, to the vague heuristics of calculating a strategy in a competition, or calculating the chance of a successful relationship between two people. For example, multiplying 7 by 6 is a simple algorithmic calculation. Extracting the square root or the cube root of a number using mathematical models is a more complex algorithmic calculation. Statistical estimations of the likely election results from opinion polls also involve algorithmic calculations, but produces ranges of possibilities rather than exact answers. To ''calculate'' means to determine mathematically in the case of a number or amount, or in the case of an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Solid Of Revolution
In geometry, a solid of revolution is a Solid geometry, solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution''), which may not Intersection (geometry), intersect the generatrix (except at its boundary). The Surface (mathematics), surface created by this revolution and which bounds the solid is the ''surface of revolution''. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area (Pappus's centroid theorem, Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylinder (geometry), cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the Disc integration, disc met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Disc Integration
Disc integration, also known in integral calculus as the disc method, is a method for calculating the volume of a solid of revolution of a solid-state material when integrating along an axis "parallel" to the axis of revolution. This method models the resulting three-dimensional shape as a stack of an infinite number of discs of varying radius and infinitesimal thickness. It is also possible to use the same principles with rings instead of discs (the "washer method") to obtain hollow solids of revolutions. This is in contrast to shell integration, that integrates along an axis ''perpendicular'' to the axis of revolution. Definition Function of If the function to be revolved is a function of , the following integral represents the volume of the solid of revolution: :\pi\int_a^b R(x)^2\,dx where is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: or some other constant). Function of If the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Double Integral
In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, or . Integrals of a function of two variables over a region in \mathbb^2 (the Real line, real-number plane) are called double integrals, and integrals of a function of three variables over a region in \mathbb^3 (real-number 3D space) are called triple integrals. For repeated antidifferentiation of a single-variable function, see the Cauchy formula for repeated integration. Introduction Just as the definite integral of a positive function of one variable represents the area of the region between the graph of the function and the -axis, the double integral of a positive function of two variables represents the volume of the region between the surface defined by the function (on the three-dimensional Cartesian plane where ) and the plane which contains its Domain of a function, domain. If there are more variables, a multiple inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Polar Coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray (geometry), ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Solid Of Revolution
In geometry, a solid of revolution is a Solid geometry, solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution''), which may not Intersection (geometry), intersect the generatrix (except at its boundary). The Surface (mathematics), surface created by this revolution and which bounds the solid is the ''surface of revolution''. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area (Pappus's centroid theorem, Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylinder (geometry), cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the Disc integration, disc met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Disc Integration
Disc integration, also known in integral calculus as the disc method, is a method for calculating the volume of a solid of revolution of a solid-state material when integrating along an axis "parallel" to the axis of revolution. This method models the resulting three-dimensional shape as a stack of an infinite number of discs of varying radius and infinitesimal thickness. It is also possible to use the same principles with rings instead of discs (the "washer method") to obtain hollow solids of revolutions. This is in contrast to shell integration, that integrates along an axis ''perpendicular'' to the axis of revolution. Definition Function of If the function to be revolved is a function of , the following integral represents the volume of the solid of revolution: :\pi\int_a^b R(x)^2\,dx where is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: or some other constant). Function of If the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Frank J
Frank, FRANK, or Franks may refer to: People * Frank (given name) * Frank (surname) * Franks (surname) * Franks, a Germanic people in late Roman times * Franks, a term in the Muslim world for all western Europeans, particularly during the Crusades Currency * Liechtenstein franc or frank, the currency of Liechtenstein since 1920 * Swiss franc or frank, the currency of Switzerland since 1850 * Westphalian frank, currency of the Kingdom of Westphalia between 1808 and 1813 * The currencies of the German-speaking cantons of Switzerland (1803–1814): ** Appenzell frank ** Aargau frank ** Basel frank ** Berne frank ** Fribourg frank ** Glarus frank ** Graubünden frank ** Luzern frank ** Schaffhausen frank ** Schwyz frank ** Solothurn frank ** St. Gallen frank ** Thurgau frank ** Unterwalden frank ** Uri frank ** Zürich frank Places * Frank, Alberta, Canada, an urban community, formerly a village * Franks, Illinois, United States, an unincorporated community ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Elliott Mendelson
Elliott Mendelson (May 24, 1931 – May 7, 2020) was an American logician. He was a professor of mathematics at Queens College of the City University of New York, and the Graduate Center, CUNY. He was Jr. Fellow, Society of Fellows, Harvard University, 1956–58. Career Mendelson earned his BA from Columbia University and PhD from Cornell University. Mendelson taught mathematics at the college level for more than 30 years, and is the author of books on logic, philosophy of mathematics, calculus, game theory and mathematical analysis. His ''Introduction to Mathematical Logic'', first published in 1964, was reviewed by Dirk van Dalen who noted that it included "a large variety of subjects that should be part of the education of any mathematics student with an interest in foundational matters." Dirk van Dalen (1969Review: Introduction to Mathematical Logic Journal of Symbolic Logic 34(1): 110,1 Books Sole author * * * * * * * Co-author * * * * Editor * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |