|
Semi-implicit Euler Method
In mathematics, the semi-implicit Euler method, also called symplectic Euler, semi-explicit Euler, Euler–Cromer, and Newton–Størmer–Verlet (NSV), is a modification of the Euler method for solving Hamilton's equations, a system of ordinary differential equations that arises in classical mechanics. It is a symplectic integrator and hence it yields better results than the standard Euler method. Origin The method has been discovered and forgotten many times, dating back to Newton's ''Principiae'', as recalled by Richard Feynman in his ''Feynman Lectures'' (Vol. 1, Sec. 9.6) In modern times, the method was rediscovered in a 1956 preprint by René De Vogelaere that, although never formally published, influenced subsequent work on higher-order symplectic methods. Setting The semi-implicit Euler method can be applied to a pair of differential equations of the form :\begin &= f(t,v) \\ &= g(t,x), \end where ''f'' and ''g'' are given functions. Here, ''x'' and ''v'' may be e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euler Integration
In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who first proposed it in his book ''Institutionum calculi integralis'' (published 1768–1770). The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size. The Euler method often serves as the basis to construct more complex methods, e.g., predictor–corrector method. Geometrical description Purpose and why it works Consider the problem of calculating the shape of an unknown curve which starts at a given point and satis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Energy Drift
In computer simulations of mechanical systems, energy drift is the gradual change in the total energy of a closed system over time. According to the laws of mechanics, the energy should be a constant of motion and should not change. However, in simulations the energy might fluctuate on a short time scale and increase or decrease on a very long time scale due to numerical integration artifacts that arise with the use of a finite time step . This is somewhat similar to the flying ice cube problem, whereby numerical errors in handling equipartition of energy can change vibrational energy into translational energy. More specifically, the energy tends to increase exponentially; its increase can be understood intuitively because each step introduces a small perturbation to the true velocity , which (if uncorrelated with , which will be true for simple integration methods) results in a second-order increase in the energy E = \sum m \mathbf^2 = \sum m \mathbf_\text^2 + \sum m \, \delta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the matrix and the linear map represented, on a given basis (linear algebra), basis, by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible matrix, invertible and the corresponding linear map is an linear isomorphism, isomorphism. However, if the determinant is zero, the matrix is referred to as singular, meaning it does not have an inverse. The determinant is completely determined by the two following properties: the determinant of a product of matrices is the product of their determinants, and the determinant of a triangular matrix is the product of its diagonal entries. The determinant of a matrix is :\begin a & b\\c & d \end=ad-bc, and the determinant of a matrix is : \begin a & b & c \\ d & e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
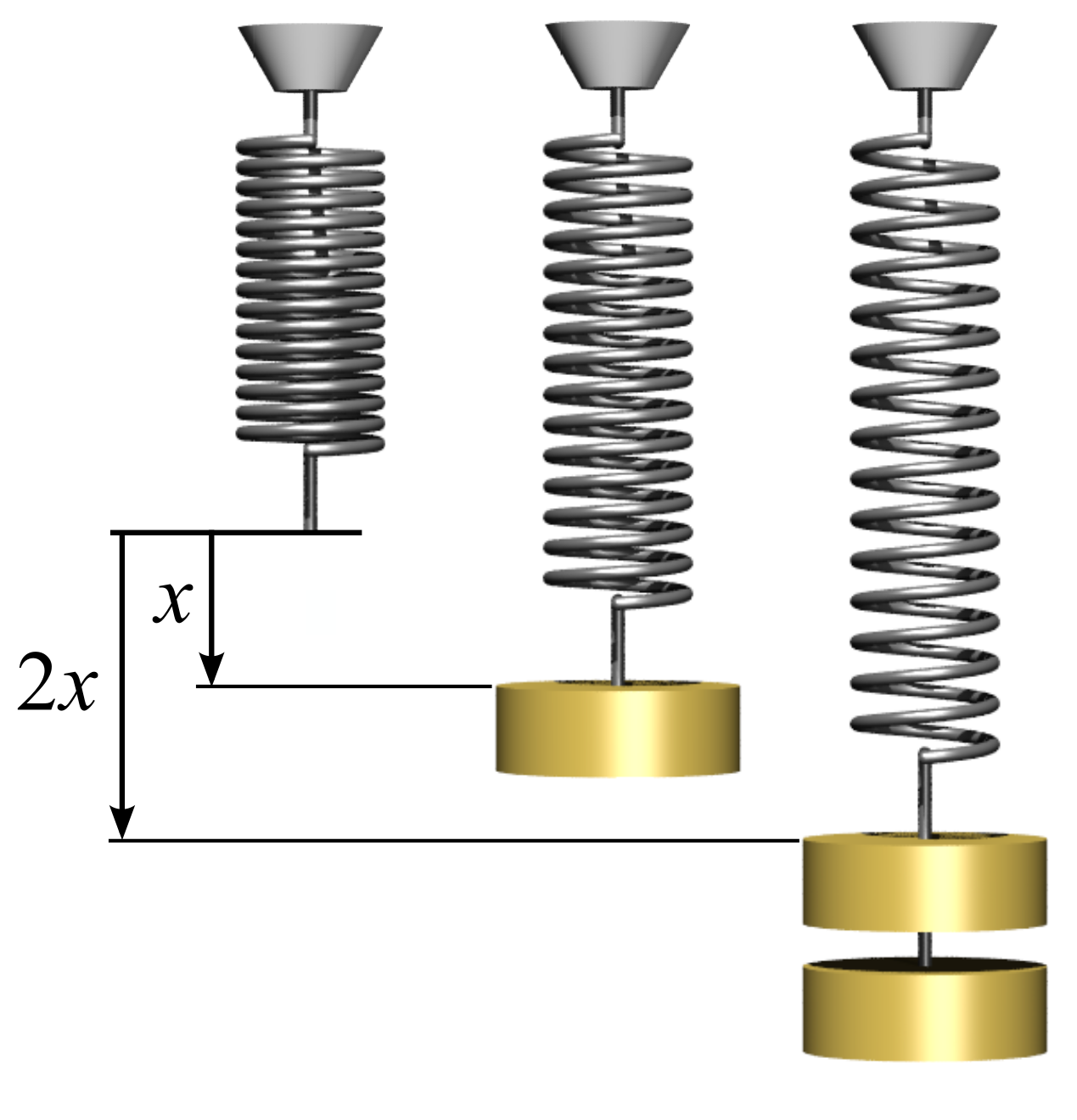
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spring (device)
A spring is a device consisting of an Elasticity (physics), elastic but largely rigid material (typically metal) bent or molded into a form (especially a coil) that can return into shape after being compressed or extended. Springs can Energy storage, store energy when compressed. In everyday use, the term most often refers to coil springs, but there are many different spring designs. Modern springs are typically manufactured from spring steel. An example of a non-metallic spring is the Bow (weapon), bow, made traditionally of flexible Taxus baccata, yew wood, which when Bow draw, drawn stores energy to propel an arrow. When a conventional spring, without stiffness variability features, is compressed or stretched from its resting position, it exerts an opposing force approximately proportional to its change in length (this approximation breaks down for larger deflections). The ''rate'' or ''spring constant'' of a spring is the change in the force it exerts, divided by the cha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symplectic Euler Stability Region
{{disambiguation ...
The term "symplectic" is a calque of "complex" introduced by Hermann Weyl in 1939. In mathematics it may refer to: * Symplectic category * Symplectic Clifford algebra, see Weyl algebra * Symplectic geometry * Symplectic group, and corresponding symplectic Lie algebra * Symplectic integrator * Symplectic manifold * Symplectic matrix * Symplectic representation * Symplectic vector space, a vector space with a symplectic bilinear form It can also refer to: * Symplectic bone, a bone found in fish skulls * Symplectite, in reference to a mineral intergrowth texture See also * Metaplectic group * Symplectomorphism In mathematics, a symplectomorphism or symplectic map is an isomorphism in the category of symplectic manifolds. In classical mechanics, a symplectomorphism represents a transformation of phase space that is volume-preserving and preserves the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Leapfrog Integration
In numerical analysis, leapfrog integration is a method for numerically integrating differential equations of the form \ddot x = \frac = A(x), or equivalently of the form \dot v = \frac = A(x), \qquad \dot x = \frac = v, particularly in the case of a dynamical system of classical mechanics. The method is known by different names in different disciplines. In particular, it is similar to the velocity Verlet method, which is a variant of Verlet integration. Leapfrog integration is equivalent to updating positions x(t) and velocities v(t)=\dot x(t) at different interleaved time points, staggered in such a way that they "leapfrog" over each other. Leapfrog integration is a second-order method, in contrast to Euler integration, which is only first-order, yet requires the same number of function evaluations per step. Unlike Euler integration, it is stable for oscillatory motion, as long as the time-step \Delta t is constant, and \Delta t < 2/\omega. Using Yoshida coefficien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Verlet Integration
Verlet integration () is a numerical method used to integrate Newton's equations of motion. It is frequently used to calculate trajectories of particles in molecular dynamics simulations and computer graphics. The algorithm was first used in 1791 by Jean Baptiste Delambre and has been rediscovered many times since then, most recently by Loup Verlet in the 1960s for use in molecular dynamics. It was also used by P. H. Cowell and A. C. C. Crommelin in 1909 to compute the orbit of Halley's Comet, and by Carl Størmer in 1907 to study the trajectories of electrical particles in a magnetic field (hence it is also called Størmer's method). The Verlet integrator provides good numerical stability, as well as other properties that are important in physical systems such as time reversibility and preservation of the symplectic form on phase space, at no significant additional computational cost over the simple Euler method. Basic Størmer–Verlet For a second-order differential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numerical Ordinary Differential Equations
Numerical methods for ordinary differential equations are methods used to find Numerical analysis, numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term can also refer to the computation of integrals. Many differential equations cannot be solved exactly. For practical purposes, however – such as in engineering – a numeric approximation to the solution is often sufficient. The algorithms studied here can be used to compute such an approximation. An alternative method is to use techniques from calculus to obtain a series expansion of the solution. Ordinary differential equations occur in many scientific disciplines, including physics, chemistry, biology, and economics. In addition, some methods in numerical partial differential equations convert the partial differential equation into an ordinary differential equation, which must then be solved. The problem A firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hamilton's Equations
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a link between classical and quantum mechanics. Overview Phase space coordinates (''p'', ''q'') and Hamiltonian ''H'' Let (M, \mathcal L) be a mechanical system with configuration space M and smooth Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''momenta''. (Also ''generalized momenta'', ''conjugate momenta'', and ''canonical momenta''). For a time inst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Discrete Mathematics
Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous functions). Objects studied in discrete mathematics include integers, Graph (discrete mathematics), graphs, and Statement (logic), statements in Mathematical logic, logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumeration, enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets (finite sets or sets with the same cardinality as the natural numbers). However, there is no exact definition of the term "discrete mathematics". The set of objects studied in discrete mathematics can be finite or infinite. The term finite mathematics is sometime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hamiltonian Mechanics
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a Hamilton–Jacobi equation, link between classical and quantum mechanics. Overview Phase space coordinates (''p'', ''q'') and Hamiltonian ''H'' Let (M, \mathcal L) be a Lagrangian mechanics, mechanical system with configuration space (physics), configuration space M and smooth Lagrangian_mechanics#Lagrangian, Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |