|
Rotor (mathematics)
A rotor is an object in the geometric algebra (also called Clifford algebra) of a vector space that represents a rotation about the origin. The term originated with William Kingdon Clifford, in showing that the quaternion algebra is just a special case of Hermann Grassmann's "theory of extension" (Ausdehnungslehre). Hestenes Hestenes uses the notation R^\dagger for the reverse. defined a rotor to be any element R of a geometric algebra that can be written as the product of an even number of unit vectors and satisfies R\tilde R = 1, where \tilde R is the "reverse" of R—that is, the product of the same vectors, but in reverse order. Definition In mathematics, a rotor in the geometric algebra of a vector space ''V'' is the same thing as an element of the spin group Spin(''V''). We define this group below. Let ''V'' be a vector space equipped with a positive definite quadratic form ''q'', and let Cl(''V'') be the geometric algebra associated to ''V''. The algebra Cl(''V'') i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometric Algebra
In mathematics, a geometric algebra (also known as a Clifford algebra) is an algebra that can represent and manipulate geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects called multivectors. Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division (though generally not by all elements) and addition of objects of different dimensions. The geometric product was first briefly mentioned by Hermann Grassmann, who was chiefly interested in developing the closely related exterior algebra. In 1878, William Kingdon Clifford greatly expanded on Grassmann's work to form what are now usually called Clifford algebras in his honor (although Clifford himself chose to call them "geometric algebras"). Clifford defined the Clifford algebra and its product as a unification of the Gras ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spin Group
In mathematics the spin group, denoted Spin(''n''), page 15 is a Lie group whose underlying manifold is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when ) :1 \to \mathbb_2 \to \operatorname(n) \to \operatorname(n) \to 1. The group multiplication law on the double cover is given by lifting the multiplication on \operatorname(n). As a Lie group, Spin(''n'') therefore shares its dimension, , and its Lie algebra with the special orthogonal group. For , Spin(''n'') is simply connected and so coincides with the universal cover of SO(''n''). The non-trivial element of the kernel is denoted −1, which should not be confused with the orthogonal transform of reflection through the origin, generally denoted −. Spin(''n'') can be constructed as a subgroup of the invertible elements in the Clifford algebra Cl(''n''). A distinct article discusses the spin representations. Use for physics models The spin group is use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generator (mathematics)
In mathematics and physics, the term generator or generating set may refer to any of a number of related concepts. The underlying concept in each case is that of a smaller set of objects, together with a set of operations that can be applied to it, that result in the creation of a larger collection of objects, called the generated set. The larger set is then said to be generated by the smaller set. It is commonly the case that the generating set has a simpler set of properties than the generated set, thus making it easier to discuss and examine. It is usually the case that properties of the generating set are in some way preserved by the act of generation; likewise, the properties of the generated set are often reflected in the generating set. List of generators A list of examples of generating sets follow. * Generating set or spanning set of a vector space: a set that spans the vector space * Generating set of a group: a subset of a group that is not contained in any sub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Euler's Formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number , one has e^ = \cos x + i \sin x, where is the base of the natural logarithm, is the imaginary unit, and and are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted ("cosine plus ''i'' sine"). The formula is still valid if is a complex number, and is also called ''Euler's formula'' in this more general case. Euler's formula is ubiquitous in mathematics, physics, chemistry, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics". When , Euler's formula may be rewritten as or , which is known as Euler's identity. History In 1714, the English mathematician Roger Cotes prese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lie Group
In mathematics, a Lie group (pronounced ) is a group (mathematics), group that is also a differentiable manifold, such that group multiplication and taking inverses are both differentiable. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additional properties it must have to be thought of as a "transformation" in the abstract sense, for instance multiplication and the taking of inverses (to allow division), or equivalently, the concept of addition and subtraction. Combining these two ideas, one obtains a continuous group where multiplying points and their inverses is continuous. If the multiplication and taking of inverses are smoothness, smooth (differentiable) as well, one obtains a Lie group. Lie groups provide a natural model for the concept of continuous symmetry, a celebrated example of which is the circle group. Rotating a circle is an example of a continuous symmetry. For an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Double Rotation
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4. In this article ''rotation'' means ''rotational displacement''. For the sake of uniqueness, rotation angles are assumed to be in the segment except where mentioned or clearly implied by the context otherwise. A "fixed plane" is a plane for which every vector in the plane is unchanged after the rotation. An "invariant plane" is a plane for which every vector in the plane, although it may be affected by the rotation, remains in the plane after the rotation. Geometry of 4D rotations Four-dimensional rotations are of two types: simple rotations and double rotations. Simple rotations A simple rotation about a rotation centre leaves an entire plane through (axis-plane) fixed. Every plane that is completely orthogonal to intersects in a certain point . For each such point is the centr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Translation (geometry)
In Euclidean geometry, a translation is a geometric transformation that moves every point of a figure, shape or space by the same Distance geometry, distance in a given direction (geometry), direction. A translation can also be interpreted as the addition of a constant vector space, vector to every point, or as shifting the Origin (mathematics), origin of the coordinate system. In a Euclidean space, any translation is an isometry. As a function If \mathbf is a fixed vector, known as the ''translation vector'', and \mathbf is the initial position of some object, then the translation function T_ will work as T_(\mathbf)=\mathbf+\mathbf. If T is a translation, then the image (mathematics), image of a subset A under the function (mathematics), function T is the translate of A by T . The translate of A by T_ is often written as A+\mathbf . Application in classical physics In classical physics, translational motion is movement that changes the Position (geometry), positio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Point (geometry)
In geometry, a point is an abstract idealization of an exact position, without size, in physical space, or its generalization to other kinds of mathematical spaces. As zero-dimensional objects, points are usually taken to be the fundamental indivisible elements comprising the space, of which one-dimensional curves, two-dimensional surfaces, and higher-dimensional objects consist. In classical Euclidean geometry, a point is a primitive notion, defined as "that which has no part". Points and other primitive notions are not defined in terms of other concepts, but only by certain formal properties, called axioms, that they must satisfy; for example, ''"there is exactly one straight line that passes through two distinct points"''. As physical diagrams, geometric figures are made with tools such as a compass, scriber, or pen, whose pointed tip can mark a small dot or prick a small hole representing a point, or can be drawn across a surface to represent a curve. A po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersecting anywhere inside or outside the figure at a ''center of rotation''. A solid figure has an infinite number of possible axes and angles of rotation, including chaotic rotation (between arbitrary orientation (geometry), orientations), in contrast to rotation around a fixed axis, rotation around a axis. The special case of a rotation with an internal axis passing through the body's own center of mass is known as a spin (or ''autorotation''). In that case, the surface intersection of the internal ''spin axis'' can be called a ''pole''; for example, Earth's rotation defines the geographical poles. A rotation around an axis completely external to the moving body is called a revolution (or ''orbit''), e.g. Earth's orbit around the Sun. The en ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conformal Geometric Algebra
Conformal geometric algebra (CGA) is the geometric algebra constructed over the resultant space of a map from points in an -dimensional base space to null vectors in . This allows operations on the base space, including reflections, rotations and translations to be represented using versors of the geometric algebra; and it is found that points, lines, planes, circles and spheres gain particularly natural and computationally amenable representations. The effect of the mapping is that generalized (i.e. including zero curvature) -spheres in the base space map onto -blades, and so that the effect of a translation (or ''any'' conformal mapping) of the base space corresponds to a rotation in the higher-dimensional space. In the algebra of this space, based on the geometric product of vectors, such transformations correspond to the algebra's characteristic sandwich operations, similar to the use of quaternions for spatial rotation in 3D, which combine very efficiently. A consequen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
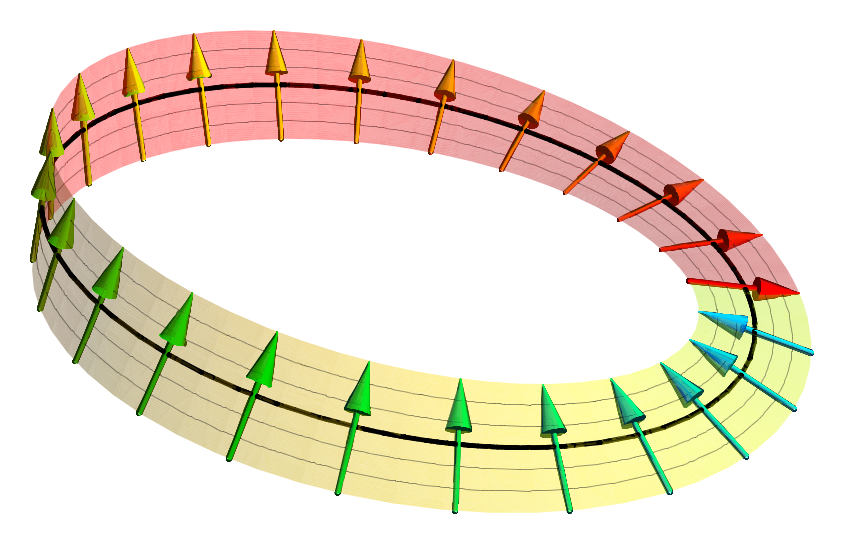
Spinor
In geometry and physics, spinors (pronounced "spinner" IPA ) are elements of a complex numbers, complex vector space that can be associated with Euclidean space. A spinor transforms linearly when the Euclidean space is subjected to a slight (infinitesimal transformation, infinitesimal) rotation, but unlike Euclidean vector, geometric vectors and tensors, a spinor transforms to its negative when the space rotates through 360° (see picture). It takes a rotation of 720° for a spinor to go back to its original state. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of Section (fiber bundle), sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |