|
Rotameter
A rotameter is a device that measures the volumetric flow rate of fluid in a closed tube. It belongs to a class of meters called variable-area flowmeters, which measure flow rate by allowing the cross-sectional area the fluid travels through to vary, causing a measurable effect. History The first variable area meter with rotating float was invented by Karl Kueppers (1874–1933) in Aachen in 1908. This is described in the German patent 215225. Felix Meyer founded the company "''Deutsche Rotawerke GmbH''" in Aachen recognizing the fundamental importance of this invention. They improved this invention with new shapes of the float and of the glass tube. Kueppers invented the special shape for the inside of the glass tube that realized a symmetrical flow scale. The brand name Rotameter was registered by the British company GEC Elliot automation, Rotameter Co. In many other countries the brand name Rotameter is registered by Rota Yokogawa GmbH & Co. KG in Germany which is now ow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thorpe Tube Flowmeter
{{Short description, Instrument to directly measure flow rate of a gas Thorpe oxygen flowmeter at a Canadian hospital (color-coded white) A Thorpe tube flowmeter, a type of variable-area flowmeter, or a rotameter, is an instrument used to directly measure the flow rate of a gas in medical instruments. It consists of a connection to a gas source, a needle valve opened and closed by turning an attached dial for control of flow rate, a float resting in a clear tapered tube, and an outlet port. It is primarily used in health care institutions during delivery of medical gases, often in conjunction with other devices such as pressure gauges or pressure reducing valves. Function When a driving pressure is applied to the inlet of a Thorpe tube flowmeter, the ball rises in the tapered tube until the flow rate creates an applied pressure on the ball equal to its weight. The tube's shape, that of a slender cone, decreases the pressure behind the ball as it rises. A cylindrical tube would n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flow Measurement
Flow measurement is the quantification of bulk fluid movement. Flow can be measured using devices called flowmeters in various ways. The common types of flowmeters with industrial applications are listed below: * Obstruction type (differential pressure or variable area) * Inferential (turbine type) * Electromagnetic * Positive displacement meter, Positive-displacement flowmeters, which accumulate a fixed volume of fluid and then count the number of times the volume is filled to measure flow. * Fluid dynamic (vortex shedding) * Anemometer * Ultrasonic flow meter * Mass flow meter (Coriolis force). Flow measurement methods other than positive-displacement flowmeters rely on forces produced by the flowing stream as it overcomes a known constriction, to indirectly calculate flow. Flow may be measured by measuring the velocity of fluid over a known area. For very large flows, tracer methods may be used to deduce the flow rate from the change in concentration of a dye or radioisotope. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
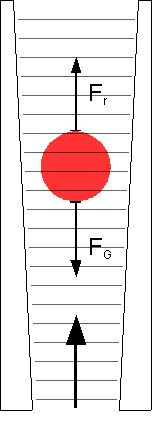
Mechanical Equilibrium
In classical mechanics, a particle is in mechanical equilibrium if the net force on that particle is zero. By extension, a physical system made up of many parts is in mechanical equilibrium if the net force on each of its individual parts is zero. In addition to defining mechanical equilibrium in terms of force, there are many alternative definitions for mechanical equilibrium which are all mathematically equivalent. * In terms of momentum, a system is in equilibrium if the momentum of its parts is all constant. * In terms of velocity, the system is in equilibrium if velocity is constant. * In a rotational mechanical equilibrium the angular momentum of the object is conserved and the net torque is zero. More generally in conservative systems, equilibrium is established at a point in Configuration space (physics), configuration space where the gradient of the potential energy with respect to the generalized coordinates is zero. If a particle in equilibrium has zero velocity, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different sightline, lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to perspective (graphical), foreshortening, nearby objects show a larger parallax than farther objects, so parallax can be used to determine distances. To measure large distances, such as the distance of a planet or a star from Earth, astronomers use the principle of parallax. Here, the term ''Stellar parallax, parallax'' is the semi-angle of inclination between two sight-lines to the star, as observed when Earth is on opposite sides of the Sun in its orbit. These distances form the lowest rung of what is called "the cosmic distance ladder", the first in a succession of methods by which astronomers determine the distances to celestial objects, serving as a basis for other distance measurements in astronomy forming the higher rungs of the ladder. Because parallax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Oscillations
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms. Oscillations occur not only in mechanical systems but also in dynamic systems in virtually every area of science: for example the beating of the human heart (for circulation), business cycles in economics, predator–prey population cycles in ecology, geothermal geysers in geology, vibration of strings in guitar and other string instruments, periodic firing of nerve cells in the brain, and the periodic swelling of Cepheid variable stars in astronomy. The term ''vibration'' is precisely used to describe a mechanical oscillation. Oscillation, especially rapid oscillation, may be an undesirable phenomenon in pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement Uncertainty
In metrology, measurement uncertainty is the expression of the statistical dispersion of the values attributed to a quantity measured on an interval or ratio scale. All measurements are subject to uncertainty and a measurement result is complete only when it is accompanied by a statement of the associated uncertainty, such as the standard deviation. By international agreement, this uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity value. It is a non-negative parameter. The measurement uncertainty is often taken as the standard deviation of a state-of-knowledge probability distribution over the possible values that could be attributed to a measured quantity. Relative uncertainty is the measurement uncertainty relative to the magnitude of a particular single choice for the value for the measured quantity, when this choice is nonzero. This particular single choice is usually called the measured value, which may be optimal in some well-defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buoyancy
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the Displacement (fluid), displaced fluid. For this reason, an object with average density greater than the surrounding fluid tends to sink because its weight is greater than the weight of the fluid it displaces. If the objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drag Equation
In fluid dynamics, the drag equation is a formula used to calculate the force of drag (physics), drag experienced by an object due to movement through a fully enclosing fluid. The equation is: F_\, =\, \tfrac12\, \rho\, u^2\, c_\, A where *F_ is the drag force, which is by definition the force component in the direction of the flow velocity, *\rho is the mass density of the fluid, *u is the flow velocity relative to the object, *A is the reference area, and *c_ is the drag coefficient – a dimensionless number, dimensionless physical coefficient, coefficient related to the object's geometry and taking into account both skin friction and form drag. If the fluid is a liquid, c_ depends on the Reynolds number; if the fluid is a gas, c_ depends on both the Reynolds number and the Mach number. The equation is attributed to Lord Rayleigh, who originally used ''L''2 in place of ''A'' (with ''L'' being some linear dimension). The reference area ''A'' is typically defined as the area of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drag (physics)
In fluid dynamics, drag, sometimes referred to as fluid resistance, is a force acting opposite to the direction of motion of any object moving with respect to a surrounding fluid. This can exist between two fluid layers, two solid surfaces, or between a fluid and a solid surface. Drag forces tend to decrease fluid velocity relative to the solid object in the fluid's path. Unlike other resistive forces, drag force depends on velocity. Drag force is proportional to the relative velocity for low-speed flow and is proportional to the velocity squared for high-speed flow. This distinction between low and high-speed flow is measured by the Reynolds number. Drag is instantaneously related to vorticity dynamics through the Josephson-Anderson relation. Examples Examples of drag include: * Net force, Net Aerodynamic force, aerodynamic or Fluid dynamics, hydrodynamic force: Drag acting opposite to the direction of movement of a solid object such as cars, aircraft, and boat hulls. * Viscou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |