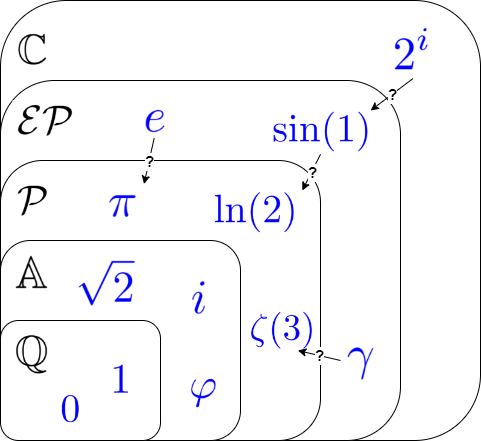
|
Ring Of Periods
In mathematics, specifically algebraic geometry, a period or algebraic period is a complex number that can be expressed as an integral of an algebraic function over an algebraic domain. The periods are a class of numbers which includes, alongside the algebraic numbers, many well known mathematical constants such as the number π. Sums and products of periods remain periods, such that the periods \mathcal P form a ring. Maxim Kontsevich and Don Zagier gave a survey of periods and introduced some conjectures about them. Periods play an important role in the theory of differential equations and transcendental numbers as well as in open problems of modern arithmetical algebraic geometry. They also appear when computing the integrals that arise from Feynman diagrams, and there has been intensive work trying to understand the connections. Definition A number \alpha is a period if it can be expressed as an integral of the form :\alpha = \int_Q(x_1,\ldots,x_n)\ \mathrmx_1\ldots\mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classes Of Numbers
Class, Classes, or The Class may refer to: Common uses not otherwise categorized * Class (biology), a taxonomic rank * Class (knowledge representation), a collection of individuals or objects * Class (philosophy), an analytical concept used differently from such group phenomena as "types" or "kinds" * Class (set theory), a collection of sets that can be unambiguously defined by a property that all its members share * Hazard class, a dangerous goods classification * Social class, the hierarchical arrangement of individuals in society, usually defined by wealth and occupation * Working class, can be defined by rank, income or collar Arts, entertainment, and media *The Class (song), "The Class" (song), 1959 Chubby Checker song *Character class in role-playing games and other genres *Class 95 (radio station), a Singaporean radio channel Films *Class (film), ''Class'' (film), 1983 American film *The Class (2007 film), ''The Class'' (2007 film), 2007 Estonian film *The Class (2008 f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rational Function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field . In this case, one speaks of a rational function and a rational fraction ''over ''. The values of the variables may be taken in any field containing . Then the domain of the function is the set of the values of the variables for which the denominator is not zero, and the codomain is . The set of rational functions over a field is a field, the field of fractions of the ring of the polynomial functions over . Definitions A function f is called a rational function if it can be written in the form : f(x) = \frac where P and Q are polynomial functions of x and Q is not the zero function. The domain of f is the set of all values of x for which the denominator Q(x) is not zero. How ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if the base is implicit, simply . Parentheses are sometimes added for clarity, giving , , or . This is done particularly when the argument to the logarithm is not a single symbol, so as to prevent ambiguity. The natural logarithm of is the exponentiation, power to which would have to be raised to equal . For example, is , because . The natural logarithm of itself, , is , because , while the natural logarithm of is , since . The natural logarithm can be defined for any positive real number as the Integral, area under the curve from to (with the area being negative when ). The simplicity of this definition, which is matched in many other formulas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definable Number
Informally, a definable real number is a real number that can be uniquely specified by its description. The description may be expressed as a construction or as a formula of a formal language. For example, the positive square root of 2, \sqrt, can be defined as the unique positive solution to the equation x^2 = 2, and it can be constructed with a compass and straightedge. Different choices of a formal language or its interpretation give rise to different notions of definability. Specific varieties of definable numbers include the constructible numbers of geometry, the algebraic numbers, and the computable numbers. Because formal languages can have only countably many formulas, every notion of definable numbers has at most countably many definable real numbers. However, by Cantor's diagonal argument, there are uncountably many real numbers, so almost every real number is undefinable. Constructible numbers One way of specifying a real number uses geometric techniques. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is ''countable'' if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements. In more technical terms, assuming the axiom of countable choice, a set is ''countable'' if its cardinality (the number of elements of the set) is not greater than that of the natural numbers. A countable set that is not finite is said to be countably infinite. The concept is attributed to Georg Cantor, who proved the existence of uncountable sets, that is, sets that are not countable; for example the set of the real numbers. A note on terminology Although the terms "countable" and "countably infinite" as def ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computable Number
In mathematics, computable numbers are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm. They are also known as the recursive numbers, effective numbers, computable reals, or recursive reals. The concept of a computable real number was introduced by Émile Borel in 1912, using the intuitive notion of computability available at the time. Equivalent definitions can be given using μ-recursive functions, Turing machines, or λ-calculus as the formal representation of algorithms. The computable numbers form a real closed field and can be used in the place of real numbers for many, but not all, mathematical purposes. Informal definition In the following, Marvin Minsky defines the numbers to be computed in a manner similar to those defined by Alan Turing in 1936; i.e., as "sequences of digits interpreted as decimal fractions" between 0 and 1: The key notions in the definition are (1) that some ''n'' is specified at the start ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number
In mathematics, a transcendental number is a real or complex number that is not algebraic: that is, not the root of a non-zero polynomial with integer (or, equivalently, rational) coefficients. The best-known transcendental numbers are and . The quality of a number being transcendental is called transcendence. Though only a few classes of transcendental numbers are known, partly because it can be extremely difficult to show that a given number is transcendental. Transcendental numbers are not rare: indeed, almost all real and complex numbers are transcendental, since the algebraic numbers form a countable set, while the set of real numbers and the set of complex numbers are both uncountable sets, and therefore larger than any countable set. All transcendental real numbers (also known as real transcendental numbers or transcendental irrational numbers) are irrational numbers, since all rational numbers are algebraic. The converse is not true: Not all irrational numbers are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality (mathematics)
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. The main types of inequality are less than and greater than (denoted by and , respectively the less-than sign, less-than and greater-than sign, greater-than signs). Notation There are several different notations used to represent different kinds of inequalities: * The notation ''a'' ''b'' means that ''a'' is greater than ''b''. In either case, ''a'' is not equal to ''b''. These relations are known as strict inequalities, meaning that ''a'' is strictly less than or strictly greater than ''b''. Equality is excluded. In contrast to strict inequalities, there are two types of inequality relations that are not strict: * The notation ''a'' ≤ ''b'' or ''a'' ⩽ ''b'' or ''a'' ≦ ''b'' means that ''a'' is less than or equal to ''b'' (or, equivalently, at most ''b'', or no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Function
In mathematics, a constant function is a function whose (output) value is the same for every input value. Basic properties As a real-valued function of a real-valued argument, a constant function has the general form or just For example, the function is the specific constant function where the output value is . The domain of this function is the set of all real numbers. The image of this function is the singleton set . The independent variable does not appear on the right side of the function expression and so its value is "vacuously substituted"; namely , , , and so on. No matter what value of is input, the output is . The graph of the constant function is a ''horizontal line'' in the plane that passes through the point . In the context of a polynomial in one variable , the constant function is called ''non-zero constant function'' because it is a polynomial of degree 0, and its general form is , where is nonzero. This function has no intersection point with the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area
Area is the measure of a region's size on a surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). Two different regions may have the same area (as in squaring the circle); by synecdoche, "area" sometimes is used to refer to the region, as in a " polygonal area". The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number
In mathematics, an algebraic number is a number that is a root of a function, root of a non-zero polynomial in one variable with integer (or, equivalently, Rational number, rational) coefficients. For example, the golden ratio (1 + \sqrt)/2 is an algebraic number, because it is a root of the polynomial X^2 - X - 1, i.e., a solution of the equation x^2 - x - 1 = 0, and the complex number 1 + i is algebraic as a root of X^4 + 4. Algebraic numbers include all integers, rational numbers, and nth root, ''n''-th roots of integers. Algebraic complex numbers are closed under addition, subtraction, multiplication and division, and hence form a field (mathematics), field, denoted \overline. The set of algebraic real numbers \overline \cap \R is also a field. Numbers which are not algebraic are called transcendental number, transcendental and include pi, and . There are countable set, countably many algebraic numbers, hence almost all real (or complex) numbers (in the sense of Lebesgue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |