|
Reliability (statistics)
In statistics and psychometrics, reliability is the overall consistency of a measure. A measure is said to have a high reliability if it produces similar results under consistent conditions:It is the characteristic of a set of test scores that relates to the amount of random error from the measurement process that might be embedded in the scores. Scores that are highly reliable are precise, reproducible, and consistent from one testing occasion to another. That is, if the testing process were repeated with a group of test takers, essentially the same results would be obtained. Various kinds of reliability coefficients, with values ranging between 0.00 (much error) and 1.00 (no error), are usually used to indicate the amount of error in the scores. For example, measurements of people's height and weight are often extremely reliable.The Marketing Accountability Standards Board (MASB) endorses this definition as part of its ongoinCommon Language: Marketing Activities and Metrics Pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Item-total Correlation
The item–total correlation is the correlation between a scored item and the total test score. It is an item statistic used in psychometric analysis to diagnose assessment items that fail to indicate the underlying psychological trait so that they can be removed or revised. The item-total correlation in item analysis In item analysis, an item–total correlation is usually calculated for each item of a scale or test to diagnose the degree to which assessment items indicate the underlying trait. Assuming that most of the items of an assessment do indicate the underlying trait, each item should have a reasonably strong positive correlation with the total score on that assessment. An important goal of item analysis is to identify and remove or revise items that are not good indicators of the underlying trait. A small or negative item-correlation provides empirical evidence that the item is not measuring the same construct measured by the assessment. Exact values depend on the type ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pearson Product-moment Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Reliability Theory
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability is defined as the probability that a product, system, or service will perform its intended function adequately for a specified period of time, OR will operate in a defined environment without failure. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The ''reliability function'' is theoretically defined as the probability of success. In practice, it is calculated using different techniques, and its value ranges between 0 and 1, where 0 indicates no probability of success while 1 indicates definite success. This probability is estimated from detailed (physics of failure) analysis, previous data sets, or through reliability testing and reliability modeling. Availability, testability, maintainability, and maint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Accuracy And Precision
Accuracy and precision are two measures of ''observational error''. ''Accuracy'' is how close a given set of measurements (observations or readings) are to their ''true value''. ''Precision'' is how close the measurements are to each other. The International Organization for Standardization (ISO) defines a related measure: ''trueness'', "the closeness of agreement between the arithmetic mean of a large number of test results and the true or accepted reference value." While ''precision'' is a description of ''random errors'' (a measure of statistical variability), ''accuracy'' has two different definitions: # More commonly, a description of ''systematic errors'' (a measure of statistical bias of a given measure of central tendency, such as the mean). In this definition of "accuracy", the concept is independent of "precision", so a particular set of data can be said to be accurate, precise, both, or neither. This concept corresponds to ISO's ''trueness''. # A combination of both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Levels Of Measurement
Level of measurement or scale of measure is a classification that describes the nature of information within the values assigned to dependent and independent variables, variables. Psychologist Stanley Smith Stevens developed the best-known classification with four levels, or scales, of measurement: #Nominal level, nominal, #Ordinal scale, ordinal, #Interval scale, interval, and #Ratio scale, ratio. This framework of distinguishing levels of measurement originated in psychology and has since had a complex history, being adopted and extended in some disciplines and by some scholars, and criticized or rejected by others. Other classifications include those by Mosteller and John Tukey, Tukey, and by Chrisman. Stevens's typology Overview Stevens proposed his typology in a 1946 ''Science (journal), Science'' article titled "On the theory of scales of measurement". In that article, Stevens claimed that all measurement in science was conducted using four different types of scales tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Homogeneity (statistics)
In statistics, homogeneity and its opposite, heterogeneity, arise in describing the properties of a dataset, or several datasets. They relate to the validity of the often convenient assumption that the statistical properties of any one part of an overall dataset are the same as any other part. In meta-analysis, which combines the data from several studies, homogeneity measures the differences or similarities between the several studies (see also Study heterogeneity). Homogeneity can be studied to several degrees of complexity. For example, considerations of homoscedasticity examine how much the variability of data-values changes throughout a dataset. However, questions of homogeneity apply to all aspects of the statistical distributions, including the location parameter. Thus, a more detailed study would examine changes to the whole of the marginal distribution. An intermediate-level study might move from looking at the variability to studying changes in the skewness. In addit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Consistency (statistics)
In statistics, consistency of procedures, such as computing confidence intervals or conducting hypothesis tests, is a desired property of their behaviour as the number of items in the data set to which they are applied increases indefinitely. In particular, consistency requires that as the dataset size increases, the outcome of the procedure approaches the correct outcome. (entries for consistency, consistent estimator, consistent test) Use of the term in statistics derives from Sir Ronald Fisher in 1922. Use of the terms ''consistency'' and ''consistent'' in statistics is restricted to cases where essentially the same procedure can be applied to any number of data items. In complicated applications of statistics, there may be several ways in which the number of data items may grow. For example, records for rainfall within an area might increase in three ways: records for additional time periods; records for additional sites with a fixed area; records for extra sites obtained by ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
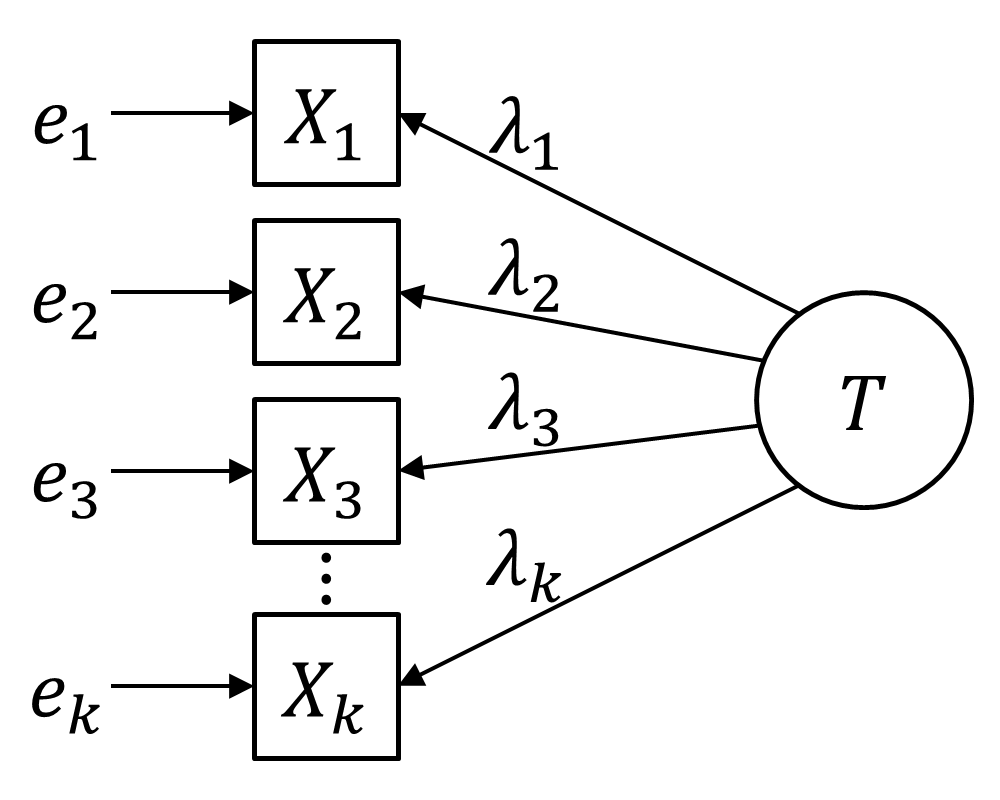
Congeneric Reliability
In statistical models applied to psychometrics, congeneric reliability \rho_C ("rho C")Cho, E. (2016). Making reliability reliable: A systematic approach to reliability coefficients. Organizational Research Methods, 19(4), 651–682. https://doi.org/10.1177/1094428116656239 a single-administration test score reliability (i.e., the reliability of persons over items holding occasion fixed) coefficient, commonly referred to as composite reliability, construct reliability, and coefficient omega. \rho_C is a structural equation model (SEM)-based reliability coefficients and is obtained from a unidimensional model. \rho_C is the second most commonly used reliability factor after tau-equivalent reliability(\rho_T; also known as Cronbach's alpha), and is often recommended as its alternative. History and names A quantity similar (but not mathematically equivalent) to congeneric reliability first appears in the appendix to McDonald's 1970 paper on factor analysis, labeled \theta.Although ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coefficient Of Variation
In probability theory and statistics, the coefficient of variation (CV), also known as normalized root-mean-square deviation (NRMSD), percent RMS, and relative standard deviation (RSD), is a standardized measure of dispersion of a probability distribution or frequency distribution. It is defined as the ratio of the standard deviation \sigma to the mean \mu (or its absolute value, , and often expressed as a percentage ("%RSD"). The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R, by economists and investors in economic models, in epidemiology, and in psychology/neuroscience. Definition The coefficient of variation (CV) is defined as the ratio of the standard deviation \sigma to the mean \mu, CV = \frac. It shows the extent of variability in relation to the mean of the population. The coefficien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Item Analysis
Within psychometrics, Item analysis refers to statistical methods used for selecting test items for inclusion in a psychological test. The concept goes back at least to . The process of item analysis varies depending on the psychometric model. For example, classical test theory or the Rasch model call for different procedures. In all cases, however, the purpose of item analysis is to produce a relatively short list of items (that is, questions to be included in an interview or questionnaire) that constitute a pure but comprehensive test of one or a few psychological constructs. To carry out the analysis, a large pool of candidate items, all of which show some degree of face validity, are given to a large sample of participants who are representative of the target population. Ideally, there should be at least 10 times as many candidate items as the desired final length of the test, and several times more people in the sample than there are items in the pool. Researchers apply a v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |