|
Quantum Hall Effect
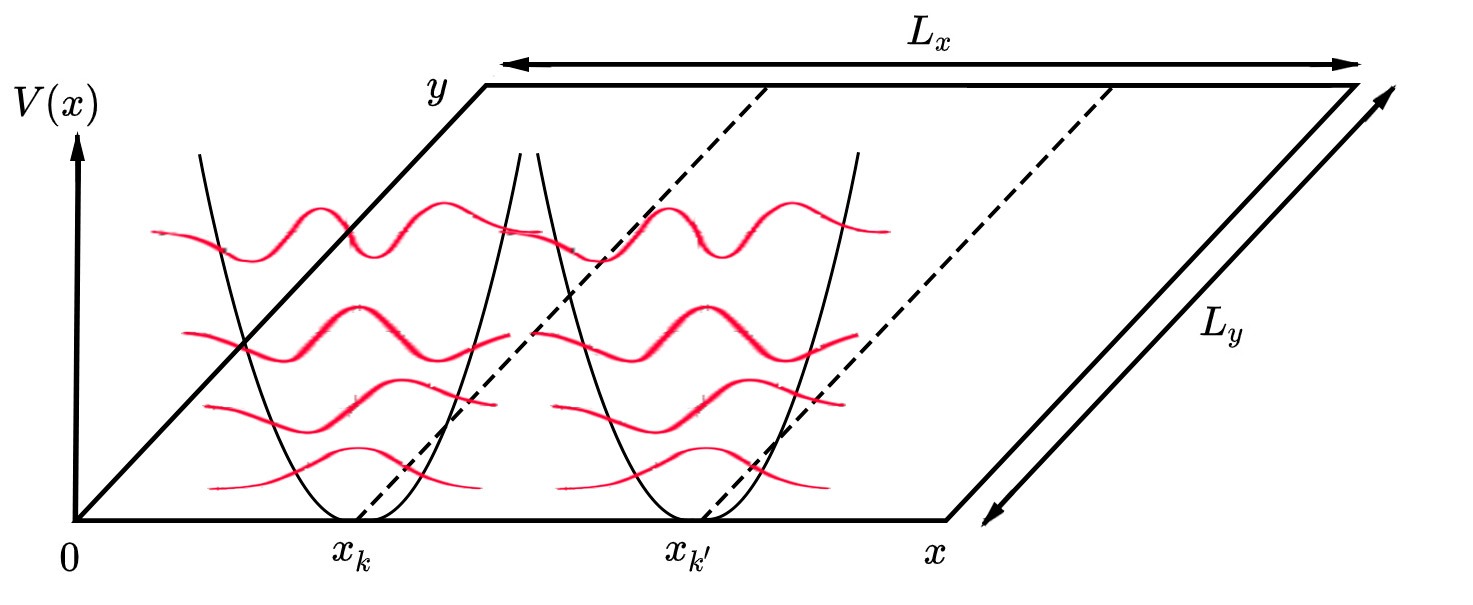
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values : R_ = \frac = \frac , where is the Hall voltage, is the channel current, is the elementary charge and is Planck's constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively. The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation corresp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary (macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limits to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klaus Von Klitzing
Klaus von Klitzing (, born 28 June 1943, Schroda) is a German physicist, known for discovery of the integer quantum Hall effect, for which he was awarded the 1985 Nobel Prize in Physics. Education In 1962, Klitzing passed the Abitur at the Artland-Gymnasium in Quakenbrück, Germany, before studying physics at the Braunschweig University of Technology, where he received his diploma in 1969. He continued his studies at the University of Würzburg at the chair of Gottfried Landwehr, completing his PhD thesis entitled ''Galvanomagnetic Properties of Tellurium in Strong Magnetic Fields'' in 1972, and gaining habilitation in 1978. Research and career During his career Klitzing has worked at the Clarendon Laboratory at the University of Oxford and the Grenoble High Magnetic Field Laboratory in France (now LNCMI), where he continued to work until becoming a professor at the Technical University of Munich in 1980. He has been a director of the Max Planck Institute for Solid State Rese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bell Labs
Nokia Bell Labs, originally named Bell Telephone Laboratories (1925–1984), then AT&T Bell Laboratories (1984–1996) and Bell Labs Innovations (1996–2007), is an American industrial research and scientific development company owned by multinational company Nokia. With headquarters located in Murray Hill, New Jersey, the company operates several laboratories in the United States and around the world. Researchers working at Bell Laboratories are credited with the development of radio astronomy, the transistor, the laser, the photovoltaic cell, the charge-coupled device (CCD), information theory, the Unix operating system, and the programming languages B, C, C++, S, SNOBOL, AWK, AMPL, and others. Nine Nobel Prizes have been awarded for work completed at Bell Laboratories. Bell Labs had its origin in the complex corporate organization of the Bell System telephone conglomerate. In the late 19th century, the laboratory began as the Western Electric Engineering Department, l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dawon Kahng
Dawon Kahng ( ko, 강대원; May 4, 1931 – May 13, 1992) was a Korean-American electrical engineer and inventor, known for his work in solid-state electronics. He is best known for inventing the MOSFET (metal–oxide–semiconductor field-effect transistor, or MOS transistor), along with his colleague Mohamed Atalla, in 1959. Kahng and Atalla developed both the PMOS and NMOS processes for MOSFET semiconductor device fabrication. The MOSFET is the most widely used type of transistor, and the basic element in most modern electronic equipment. Kahng and Atalla later proposed the concept of the MOS integrated circuit, and they did pioneering work on Schottky diodes and nanolayer-base transistors in the early 1960s. Kahng then invented the floating-gate MOSFET (FGMOS) with Simon Min Sze in 1967. Kahng and Sze proposed that FGMOS could be used as floating-gate memory cells for non-volatile memory (NVM) and reprogrammable read-only memory (ROM), which became the basis for EPROM ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mohamed Atalla
Mohamed M. Atalla ( ar, محمد عطاالله; August 4, 1924 – December 30, 2009) was an Egyptian-American engineer, physicist, cryptographer, inventor and entrepreneur. He was a semiconductor pioneer who made important contributions to modern electronics. He is best known for inventing the MOSFET (metal–oxide–semiconductor field-effect transistor, or MOS transistor) in 1959 (along with his colleague Dawon Kahng), which along with Atalla's earlier surface passivation and thermal oxidation processes, revolutionized the electronics industry. He is also known as the founder of the data security company Atalla Corporation (now Utimaco Atalla), founded in 1972. He received the Stuart Ballantine Medal (now the Benjamin Franklin Medal in physics) and was inducted into the National Inventors Hall of Fame for his important contributions to semiconductor technology as well as data security. Born in Port Said, Egypt, he was educated at Cairo University in Egypt and then Purdue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Field-effect Transistor
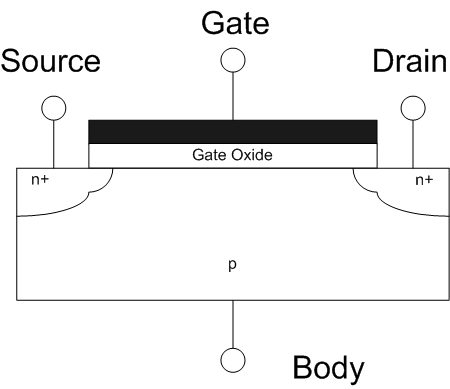
The field-effect transistor (FET) is a type of transistor that uses an electric field to control the flow of current in a semiconductor. FETs (JFETs or MOSFETs) are devices with three terminals: ''source'', ''gate'', and ''drain''. FETs control the flow of current by the application of a voltage to the gate, which in turn alters the conductivity between the drain and source. FETs are also known as unipolar transistors since they involve single-carrier-type operation. That is, FETs use either electrons (n-channel) or holes (p-channel) as charge carriers in their operation, but not both. Many different types of field effect transistors exist. Field effect transistors generally display very high input impedance at low frequencies. The most widely used field-effect transistor is the MOSFET (metal-oxide-semiconductor field-effect transistor). History The concept of a field-effect transistor (FET) was first patented by Austro-Hungarian physicist Julius Edgar Lilienfeld in 192 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MOSFET
The metal–oxide–semiconductor field-effect transistor (MOSFET, MOS-FET, or MOS FET) is a type of field-effect transistor (FET), most commonly fabricated by the controlled oxidation of silicon. It has an insulated gate, the voltage of which determines the conductivity of the device. This ability to change conductivity with the amount of applied voltage can be used for amplifying or switching electronic signals. A metal-insulator-semiconductor field-effect transistor (MISFET) is a term almost synonymous with MOSFET. Another synonym is IGFET for insulated-gate field-effect transistor. The basic principle of the field-effect transistor was first patented by Julius Edgar Lilienfeld in 1925.Lilienfeld, Julius Edgar (1926-10-08) "Method and apparatus for controlling electric currents" upright=1.6, Two power MOSFETs in V_in_the_''off''_state,_and_can_conduct_a_continuous_current_of_30 surface-mount_packages._Operating_as_switches,_each_of_these_components_can_su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Fermions
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena. Vortices are an example of topological defect, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices. Classical vortices are relevant to the Berezenskii–Kosterlitz–Thouless transition in two-dimensional XY model. Description When electrons are confined to two dimensions, cooled to very low temperatures, and subjected to a strong magnetic field, their kinetic energy is quenched due to Landau level quantization. Their behavior under such conditions is governed by the Coulomb repulsion alone, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chern–Simons Theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type developed by Edward Witten. It was discovered first by mathematical physicist Albert Schwarz. It is named after mathematicians Shiing-Shen Chern and James Harris Simons, who introduced the Chern–Simons 3-form. In the Chern–Simons theory, the action is proportional to the integral of the Chern–Simons 3-form. In condensed-matter physics, Chern–Simons theory describes the topological order in fractional quantum Hall effect states. In mathematics, it has been used to calculate knot invariants and three-manifold invariants such as the Jones polynomial. Particularly, Chern–Simons theory is specified by a choice of simple Lie group G known as the gauge group of the theory and also a number referred to as the ''level'' of the theory, which is a constant that multiplies the action. The action is gauge dependent, however the partition function of the quantum theory is well-defined wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics, a classical anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking parameter goes to zero. Perhaps the first known anomaly was the dissipative anomaly in turbulence: time-reversibility remains broken (and energy dissipation rate finite) at the limit of vanishing viscosity. In quantum theory, the first anomaly discovered was the Adler–Bell–Jackiw anomaly, wherein the axial vector current is conserved as a classical symmetry of electrodynamics, but is broken by the quantized theory. The relationship of this anomaly to the Atiyah–Singer index theorem was one of the celebrated achievements of the theory. Technically, an anomalous symmetry in a quantum theory is a symmetry of the action, but not of the measure, and so not of the partition fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gauge Invariance
In physics, a gauge theory is a type of field theory in which the Lagrangian (and hence the dynamics of the system itself) does not change (is invariant) under local transformations according to certain smooth families of operations ( Lie groups). The term ''gauge'' refers to any specific mathematical formalism to regulate redundant degrees of freedom in the Lagrangian of a physical system. The transformations between possible gauges, called ''gauge transformations'', form a Lie group—referred to as the '' symmetry group'' or the ''gauge group'' of the theory. Associated with any Lie group is the Lie algebra of group generators. For each group generator there necessarily arises a corresponding field (usually a vector field) called the ''gauge field''. Gauge fields are included in the Lagrangian to ensure its invariance under the local group transformations (called ''gauge invariance''). When such a theory is quantized, the quanta of the gauge fields are called '' gauge bo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |