|
Quadratic Equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the Expression (mathematics), expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex number, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in education, to the study of algebraic structures such as groups, rings, and fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, some having "algebra" in their name, such as commutative algebra, and some not, such as Galois theory. The word ''algebra'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\[1ex] & = \underbrace_ \times \underbrace_ \\[1ex] & = b^n \times b^m \end In other words, when multiplying a base raised to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Muller's Method
Muller's method is a root-finding algorithm, a numerical method for solving equations of the form ''f''(''x'') = 0. It was first presented by David E. Muller in 1956. Muller's method is based on the secant method, which constructs at every iteration a line through two points on the graph of ''f''. Instead, Muller's method uses three points, constructs the parabola through these three points, and takes the intersection of the ''x''-axis with the parabola to be the next approximation. Recurrence relation Muller's method is a recursive method which generates an approximation of the root ξ of ''f'' at each iteration. Starting with the three initial values ''x''0, ''x''−1 and ''x''−2, the first iteration calculates the first approximation ''x''1, the second iteration calculates the second approximation ''x''2, the third iteration calculates the third approximation ''x''3, etc. Hence the ''k''''th'' iteration generates approximation ''x''''k''. Each iteration takes as input the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because . Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'', which is denoted by \sqrt, where the symbol \sqrt is called the ''radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case 9. For nonnegative , the principal square root can also be written in exponent notation, as . Every positive number has two square roots: \sqrt, which is positive, and -\sqrt, which is negative. The two roots can be written more concisely using the ± sign as \plusmn\sqrt. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
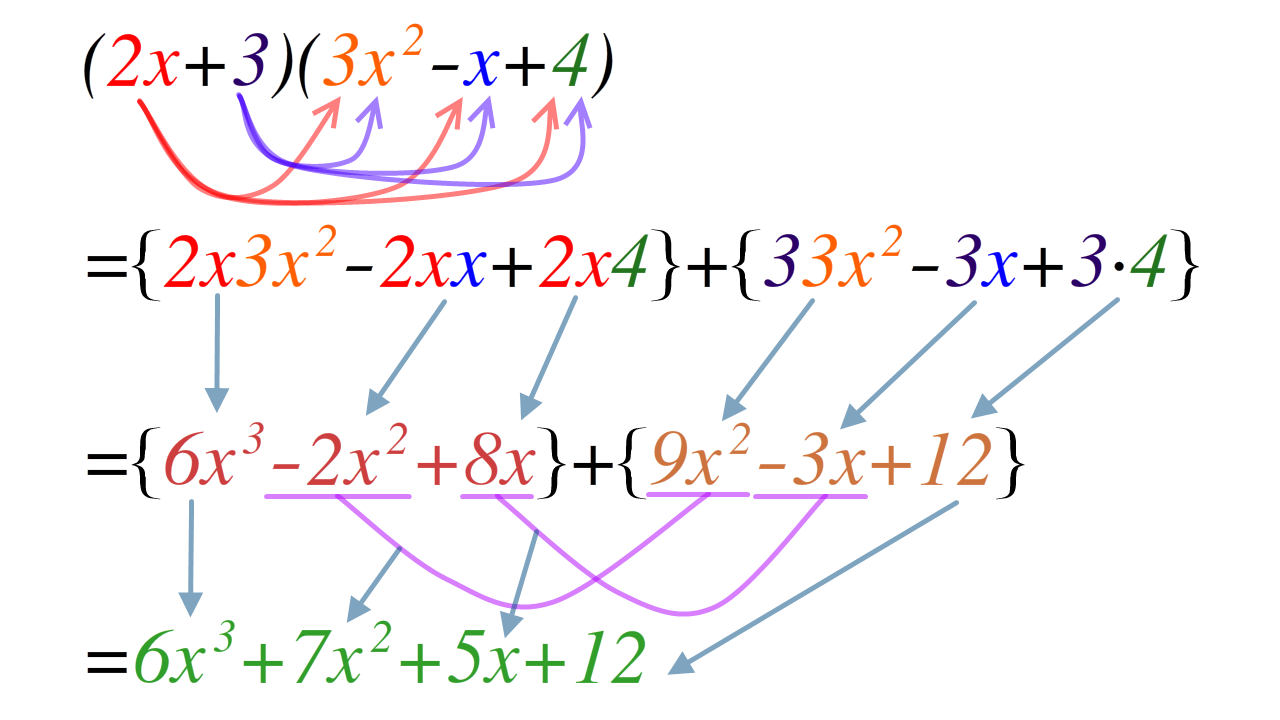
Polynomial Expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such as grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols. Simple examples of polynomial expansions are the wel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Proof
A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work. Proofs employ logic expressed in mathematical symbols ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Formula
In elementary algebra, the quadratic formula is a formula that provides the solution(s) to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as factoring (direct factoring, grouping, AC method), completing the square, graphing and others. Given a general quadratic equation of the form :ax^2+bx+c=0 with representing an unknown, with , and representing constants, and with , the quadratic formula is: :x = \frac where the plus–minus symbol "±" indicates that the quadratic equation has two solutions. Written separately, they become: : x_1=\frac\quad\text\quad x_2=\frac Each of these two solutions is also called a root (or zero) of the quadratic equation. Geometrically, these roots represent the -values at which ''any'' parabola, explicitly given as , crosses the -axis. As well as being a formula that yields the zeros of any parabola, the quadratic formula can also be used to identify the axis of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plus–minus Sign
The plus–minus sign, , is a mathematical symbol with multiple meanings. *In mathematics, it generally indicates a choice of exactly two possible values, one of which is obtained through addition and the other through subtraction. *In experimental sciences, the sign commonly indicates the confidence interval or uncertainty bounding a range of possible errors in a measurement, often the standard deviation or standard error. The sign may also represent an inclusive range of values that a reading might have. *In medicine, it means "with or without". *In engineering, the sign indicates the tolerance, which is the range of values that are considered to be acceptable, safe, or which comply with some standard or with a contract. *In botany, it is used in morphological descriptions to notate "more or less". *In chemistry, the sign is used to indicate a racemic mixture. *In chess, the sign indicates a clear advantage for the white player; the complementary minus-or-plus sign, , indicate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a Heuristic (computer science), heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vieta's Formulas
In mathematics, Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots. They are named after François Viète (more commonly referred to by the Latinised form of his name, "Franciscus Vieta"). Basic formulas Any general polynomial of degree ''n'' :P(x) = a_nx^n + a_x^ + \cdots + a_1 x + a_0 (with the coefficients being real or complex numbers and ) has (not necessarily distinct) complex roots by the fundamental theorem of algebra. Vieta's formulas relate the polynomial's coefficients to signed sums of products of the roots as follows: :\begin r_1 + r_2 + \dots + r_ + r_n = -\dfrac \\ (r_1 r_2 + r_1 r_3+\cdots + r_1 r_n) + (r_2r_3 + r_2r_4+\cdots + r_2r_n)+\cdots + r_r_n = \dfrac \\ \quad \vdots \\ r_1 r_2 \dots r_n = (-1)^n \dfrac. \end Vieta's formulas can equivalently be written as : \sum_ \left(\prod_^k r_\right)=(-1)^k\frac for (the indices are sorted in increasing order to ensure each product of roots is used exactly once). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficients
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves variables, they may also be called parameters. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. The constant coefficient is the coefficient not attached to variables in an expression. For example, the constant coefficients of the expressions above are the number 3 and the parameter ''c'', respectively. The coefficient attached to the highest degree of the variable in a polynomial is referred to as the leading coefficient. For example, in the expressions above, the leading coefficients are 2 and ''a'', respectively. Terminology and definition In mathematics, a coefficient is a multiplicative factor in some term of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |