|
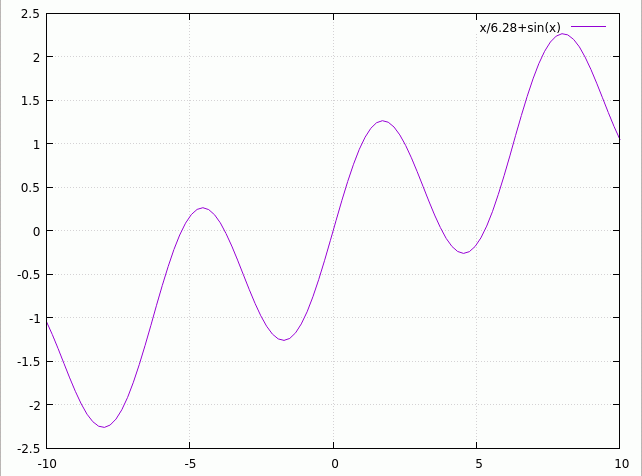
Quasiperiodic Function
In mathematics, a quasiperiodic function is a function that has a certain similarity to a periodic function. A function f is quasiperiodic with quasiperiod \omega if f(z + \omega) = g(z,f(z)), where g is a "''simpler''" function than f. What it means to be "''simpler''" is vague. A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation: :f(z + \omega) = f(z) + C Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation: :f(z + \omega) = C f(z) An example of this is the Jacobi theta function, where :\vartheta(z+\tau;\tau) = e^\vartheta(z;\tau), shows that for fixed \tau it has quasiperiod \tau; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Weierstrass Zeta Function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass. The relation between the sigma, zeta, and \wp functions is analogous to that between the sine, cotangent, and squared cosecant functions: the logarithmic derivative of the sine is the cotangent, whose derivative is negative the squared cosecant. Weierstrass sigma function The Weierstrass sigma function associated to a two-dimensional lattice \Lambda\subset\Complex is defined to be the product : \begin \operatorname &= z\prod_\left(1-\frac\right) \exp\left(\frac zw + \frac12\left(\frac zw\right)^2\right) \\ mu&= z\prod_^\infty \left(1 - \frac\right) \exp \end where \Lambda^ denotes \Lambda-\ and (\omega_1,\omega_2) is a ''fundamental pair of periods''. Through careful manipulation of the Weierstrass factorization theorem as it relates also to the sine function, another potentially more manageable inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
PlanetMath
PlanetMath is a free content, free, collaborative, mathematics online encyclopedia. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org, Ltd". PlanetMath was started when the popular free online mathematics encyclopedia MathWorld was temporarily taken offline for 12 months by a court injunction as a result of the CRC Press lawsuit against the Wolfram Research company and its employee (and MathWorld's author) Eric Weisstein. Materials The main PlanetMath focus is on encyclopedia, encyclopedic entries. It formerly operated a self-hosted forum, but now encourages discussion via Gitter. An all-inclusive PlanetMath ''Free Encyclopedia'' book of 2,300 pages is available for the encyclopedia contents up to 2006 as a free download PDF file. Content development model PlanetMath implements a specific content creation system called ''authority model''. An author who starts a ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is motion on a torus that never comes back to the same point. This behavior can also be called quasiperiodic evolution, dynamics, or flow. The torus may be a generalized torus so that the neighborhood of any point is more than two-dimensional. At each point of the torus there is a direction of motion that remains on the torus. Once a flow on a torus is defined or fixed, it determines trajectories. If the trajectories come back to a given point after a certain time then the motion is periodic with that period, otherwise it is quasiperiodic. The quasiperiodic motion is characterized by a finite set of frequencies which can be thought of as the frequencies at which the motion goes around the torus in different directions. For instance, if the torus is the surface of a doughnut, then there is the frequency at which the motion goes around the doughnut and the frequency at which it goes inside and out. But the set of frequenci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Irrational Number
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the case of irrational numbers, the decimal expansion does not terminate, nor end ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rational Number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example, The set of all rational numbers is often referred to as "the rationals", and is closed under addition, subtraction, multiplication, and division by a nonzero rational number. It is a field under these operations and therefore also called the field of rationals or the field of rational numbers. It is usually denoted by boldface , or blackboard bold A rational number is a real number. The real numbers that are rational are those whose decimal expansion either terminates after a finite number of digits (example: ), or eventually begins to repeat the same finite sequence of digits over and over (example: ). This statement is true not only in base 10, but also in every other integer base, such as the binary and hexadecimal ones (see ). A real n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quasiperiodicity
Quasiperiodicity is the property of a system that displays irregular periodicity. Periodic behavior is defined as recurring at regular intervals, such as "every 24 hours". Quasiperiodic behavior is almost but not quite periodic. The term used to denote oscillations that appear to follow a regular pattern but which do not have a fixed period. The term thus used does not have a precise definition and should not be confused with more strictly defined mathematical concepts such as an almost periodic function or a quasiperiodic function. Climatology Climate oscillations that appear to follow a regular pattern but which do not have a fixed period are called ''quasiperiodic''.''The meteorological glossary: 2d ed.'' 1930. Meteorological Office, Great Britain. "Certain phenomena which recur more or less regularly but without the exactness of truly periodic phenomena are termed quasi-periodic." Within a dynamical system such as the ocean-atmosphere system, oscillations may occur regular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Almost Periodic Function
In mathematics, an almost periodic function is, loosely speaking, a function of a real variable that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov, Hermann Weyl and Abram Samoilovitch Besicovitch, amongst others. There is also a notion of almost periodic functions on locally compact abelian groups, first studied by John von Neumann. Almost periodicity is a property of dynamical systems that appear to retrace their paths through phase space, but not exactly. An example would be a planetary system, with planets in orbits moving with periods that are not commensurable (i.e., with a period vector that is not proportional to a vector of integers). A theorem of Kronecker from diophantine approximation can be used to show that any particular configuration that occurs once, will recur to within any specified accuracy: if we wai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Floquet Theory
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the form :\dot = A(t) x, with x\in and \displaystyle A(t) \in being a piecewise continuous periodic function with period T and defines the state of the stability of solutions. The main theorem of Floquet theory, Floquet's theorem, due to , gives a canonical form for each fundamental matrix solution of this common linear system. It gives a coordinate change \displaystyle y=Q^(t)x with \displaystyle Q(t+2T)=Q(t) that transforms the periodic system to a traditional linear system with constant, real coefficients. When applied to physical systems with periodic potentials, such as crystals in condensed matter physics, the result is known as Bloch's theorem. Note that the solutions of the linear differential equation form a vector space. A matrix \phi\,(t) is called a '' fundamental matrix solution'' if the columns form a basi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bloch's Theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, who discovered the theorem in 1929. Mathematically, they are written where \mathbf is position, \psi is the wave function, u is a periodic function with the same periodicity as the crystal, the wave vector \mathbf is the crystal momentum vector, e is Euler's number, and i is the imaginary unit. Functions of this form are known as Bloch functions or Bloch states, and serve as a suitable basis for the wave functions or states of electrons in crystalline solids. The description of electrons in terms of Bloch functions, termed Bloch electrons (or less often ''Bloch Waves''), underlies the concept of electronic band structures. These eigenstates are written with subscripts as \psi_, where n is a discrete index, called the band index, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Weierstrass Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions is also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions, i.e., meromorphic functions that are doubly periodic. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Motivation A cubic of the form C_^\mathbb=\ , where g_2,g_3\in\mathbb are complex numbers with g_2^3-27g_3^2\neq0, cannot be rationally parameterized. Yet one still wants to find a way to parameterize it. For the quadric K=\left\; the unit circle, there exists a (non-rational) parameterization using the sine function and its derivative the cosine functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |