|
Quadratic Model
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the Expression (mathematics), expression on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two complex number, c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the areas of mathematics, broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variable (mathematics), variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in mathematical education, education, to the study of algebraic structures such as group (mathematics), groups, ring (mathematics), rings, and field (mathematics), fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\ ex& = \underbrace_ \times \underbrace_ \\ ex& = b^n \times b^m \end In other words, when multiplying a base raised to one e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Muller's Method
Muller's method is a root-finding algorithm, a numerical method for solving equations of the form ''f''(''x'') = 0. It was first presented by David E. Muller in 1956. Muller's method is based on the secant method, which constructs at every iteration a line through two points on the graph of ''f''. Instead, Muller's method uses three points, constructs the parabola through these three points, and takes the intersection of the ''x''-axis with the parabola to be the next approximation. Recurrence relation Muller's method is a recursive method which generates an approximation of the root ξ of ''f'' at each iteration. Starting with the three initial values ''x''0, ''x''−1 and ''x''−2, the first iteration calculates the first approximation ''x''1, the second iteration calculates the second approximation ''x''2, the third iteration calculates the third approximation ''x''3, etc. Hence the ''k''''th'' iteration generates approximation ''x''''k''. Each iteration takes as input th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because . Every nonnegative real number has a unique nonnegative square root, called the ''principal square root'', which is denoted by \sqrt, where the symbol \sqrt is called the '' radical sign'' or ''radix''. For example, to express the fact that the principal square root of 9 is 3, we write \sqrt = 3. The term (or number) whose square root is being considered is known as the ''radicand''. The radicand is the number or expression underneath the radical sign, in this case 9. For nonnegative , the principal square root can also be written in exponent notation, as . Every positive number has two square roots: \sqrt, which is positive, and -\sqrt, which is negative. The two roots can be written more concisely using the ± sign as \plusmn\sq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
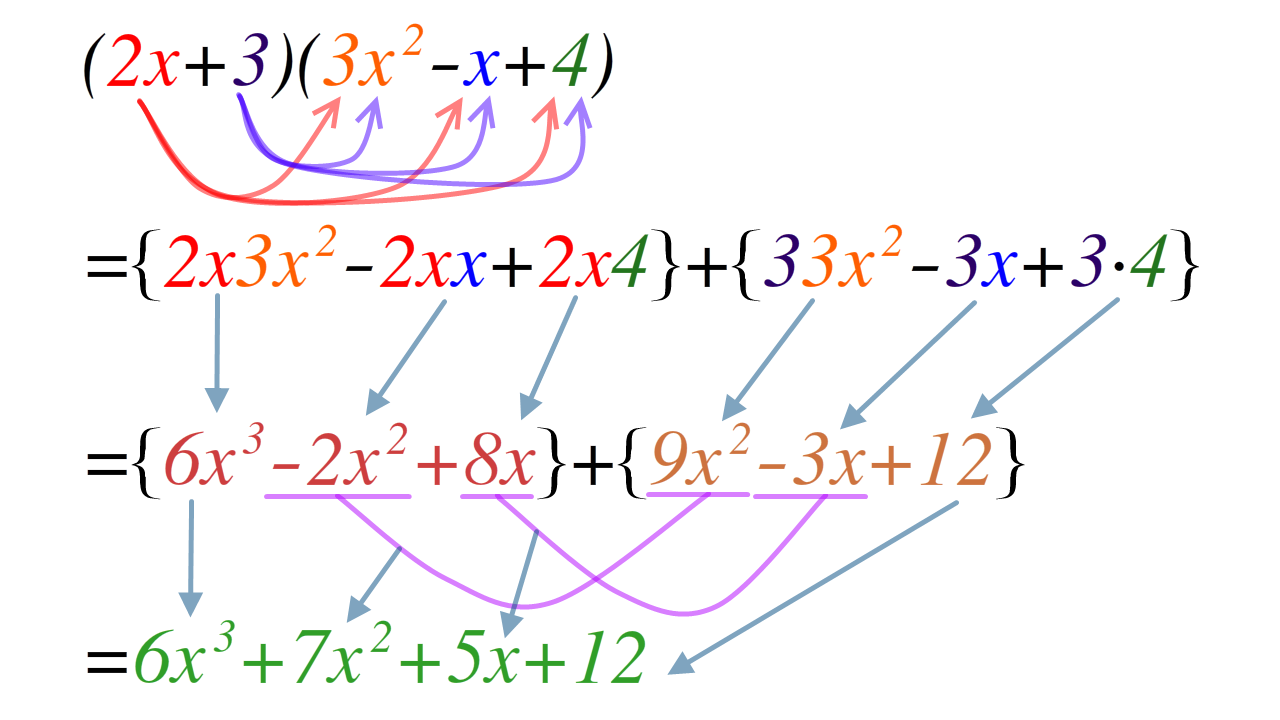
Polynomial Expansion
In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression becomes a sum of (repeated) products. During the expansion, simplifications such as grouping of like terms or cancellations of terms may also be applied. Instead of multiplications, the expansion steps could also involve replacing powers of a sum of terms by the equivalent expression obtained from the binomial formula; this is a shortened form of what would happen if the power were treated as a repeated multiplication, and expanded repeatedly. It is customary to reintroduce powers in the final result when terms involve products of identical symbols. Simple examples of polynomial expansions are the w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|