|
Pseudo-Riemannian
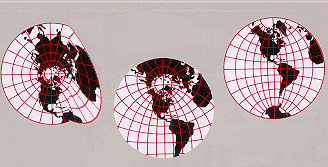
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed. Every tangent space of a pseudo-Riemannian manifold is a pseudo-Euclidean vector space. A special case used in general relativity is a four-dimensional Lorentzian manifold for modeling spacetime, where tangent vectors can be classified as timelike, null, and spacelike. Introduction Manifolds In differential geometry, a differentiable manifold is a space which is locally similar to a Euclidean space. In an ''n''-dimensional Euclidean space any point can be specified by ''n'' real numbers. These are called the coordinates of the point. An ''n''-dimensional differentiable manifold is a generalisation of ''n''-dimensional Euclidean space. In a manifold it may only be possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Levi-Civita Connection
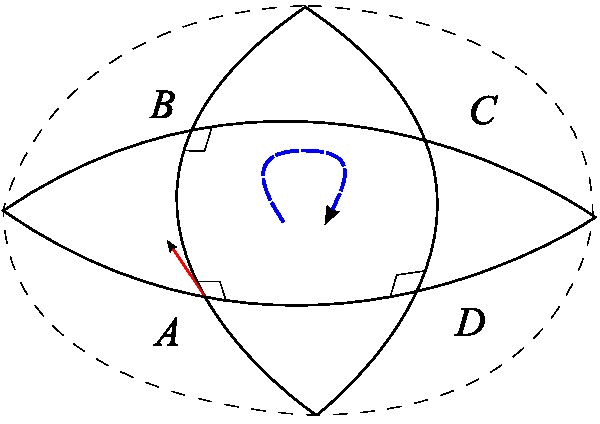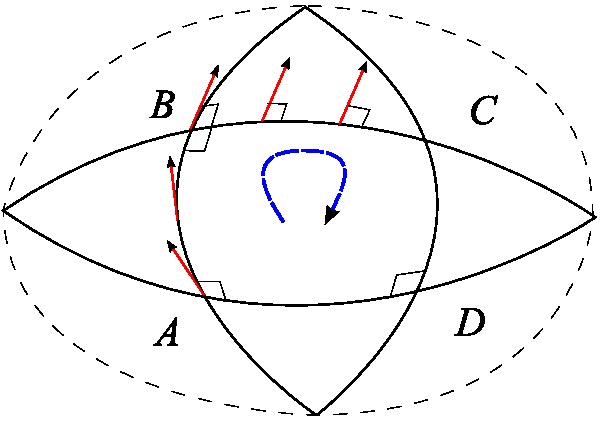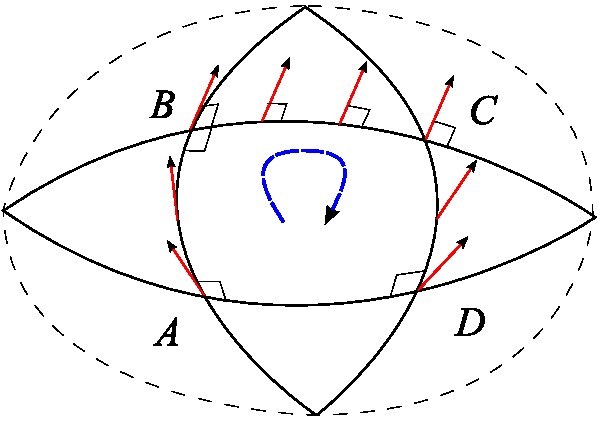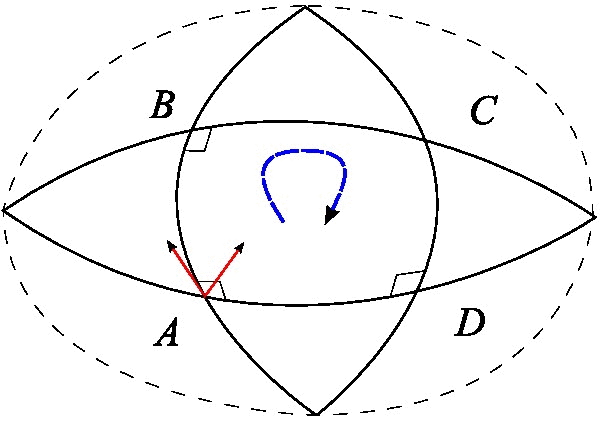
In Riemannian or pseudo Riemannian geometry (in particular the Lorentzian geometry of general relativity), the Levi-Civita connection is the unique affine connection on the tangent bundle of a manifold (i.e. affine connection) that preserves the ( pseudo-) Riemannian metric and is torsion-free. The fundamental theorem of Riemannian geometry states that there is a unique connection which satisfies these properties. In the theory of Riemannian and pseudo-Riemannian manifolds the term covariant derivative is often used for the Levi-Civita connection. The components (structure coefficients) of this connection with respect to a system of local coordinates are called Christoffel symbols. History The Levi-Civita connection is named after Tullio Levi-Civita, although originally "discovered" by Elwin Bruno Christoffel. Levi-Civita, along with Gregorio Ricci-Curbastro, used Christoffel's symbols to define the notion of parallel transport and explore the relationship of paral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point of is a bilinear form defined on the tangent space at (that is, a bilinear function that maps pairs of tangent vectors to real numbers), and a metric tensor on consists of a metric tensor at each point of that varies smoothly with . A metric tensor is ''positive-definite'' if for every nonzero vector . A manifold equipped with a positive-definite metric tensor is known as a Riemannian manifold. Such a metric tensor can be thought of as specifying ''infinitesimal'' distance on the manifold. On a Riemannian manifold , the length of a smooth curve between two points and can be defined by integration, and the distance between and can be defined ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Metric
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invariant. Beca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiable Manifold
In mathematics, a differentiable manifold (also differential manifold) is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible (namely, the transition from one chart to another is differentiable), then computations done in one chart are valid in any other differentiable chart. In formal terms, a differentiable manifold is a topological manifold with a globally defined differential structure. Any topological manifold can be given a differential structure locally by using the homeomorphisms in its atlas and the standard differential structure on a vector space. To induce a global differential structure on the local coordinate systems induced by the homeomorphisms, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Minkowski Space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invariant. Beca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Riemannian Geometry
In the mathematical field of Riemannian geometry, the fundamental theorem of Riemannian geometry states that on any Riemannian manifold (or pseudo-Riemannian manifold) there is a unique affine connection that is torsion-free and metric-compatible, called the ''Levi-Civita connection'' or ''Riemannian connection'' of the given metric. Because it is canonically defined by such properties, often this connection is automatically used when given a metric. Statement of the theorem Fundamental theorem of Riemannian Geometry. Let be a Riemannian manifold (or pseudo-Riemannian manifold). Then there is a unique connection which satisfies the following conditions: * for any vector fields , , and we have X \big(g(Y,Z)\big) = g( \nabla_X Y,Z ) + g( Y,\nabla_X Z ), where denotes the derivative of the function along vector field . * for any vector fields , , \nabla_XY-\nabla_YX= ,Y where denotes the Lie bracket of and . The first condition is called ''metric-compatibility'' of . It may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
General Relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics. General relativity generalizes special relativity and refines Newton's law of universal gravitation, providing a unified description of gravity as a geometric property of space and time or four-dimensional spacetime. In particular, the ' is directly related to the energy and momentum of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of second order partial differential equations. Newton's law of universal gravitation, which describes classical gravity, can be seen as a prediction of general relativity for the almost flat spacetime geometry around stationary mass distributions. Some predictions of general relativity, however, are beyond Newton's law of universal gra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Curvature Tensor
In the mathematical field of differential geometry, the Riemann curvature tensor or Riemann–Christoffel tensor (after Bernhard Riemann and Elwin Bruno Christoffel) is the most common way used to express the curvature of Riemannian manifolds. It assigns a tensor to each point of a Riemannian manifold (i.e., it is a tensor field). It is a local invariant of Riemannian metrics which measures the failure of the second covariant derivatives to commute. A Riemannian manifold has zero curvature if and only if it is ''flat'', i.e. locally isometric to the Euclidean space. The curvature tensor can also be defined for any pseudo-Riemannian manifold, or indeed any manifold equipped with an affine connection. It is a central mathematical tool in the theory of general relativity, the modern theory of gravity, and the curvature of spacetime is in principle observable via the geodesic deviation equation. The curvature tensor represents the tidal force experienced by a rigid body moving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metric Signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative and zero eigenvalues of the real symmetric matrix of the metric tensor with respect to a basis. In relativistic physics, the ''v'' represents the time or virtual dimension, and the ''p'' for the space and physical dimension. Alternatively, it can be defined as the dimensions of a maximal positive and null subspace. By Sylvester's law of inertia these numbers do not depend on the choice of basis. The signature thus classifies the metric up to a choice of basis. The signature is often denoted by a pair of integers implying ''r''= 0, or as an explicit list of signs of eigenvalues such as or for the signatures and , respectively. The signature is said to be indefinite or mixed if both ''v'' and ''p'' are nonzero, and degenerate if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-degenerate Bilinear Form
In mathematics, specifically linear algebra, a degenerate bilinear form on a vector space ''V'' is a bilinear form such that the map from ''V'' to ''V''∗ (the dual space of ''V'' ) given by is not an isomorphism. An equivalent definition when ''V'' is finite-dimensional is that it has a non-trivial kernel: there exist some non-zero ''x'' in ''V'' such that :f(x,y)=0\, for all \,y \in V. Nondegenerate forms A nondegenerate or nonsingular form is a bilinear form that is not degenerate, meaning that v \mapsto (x \mapsto f(x,v)) is an isomorphism, or equivalently in finite dimensions, if and only if :f(x,y)=0 for all y \in V implies that x = 0. The most important examples of nondegenerate forms are inner products and symplectic forms. Symmetric nondegenerate forms are important generalizations of inner products, in that often all that is required is that the map V \to V^* be an isomorphism, not positivity. For example, a manifold with an inner product structure on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |