|
Proper Class
Proper may refer to: Mathematics * Proper map, in topology, a property of continuous function between topological spaces, if inverse images of compact subsets are compact * Proper morphism, in algebraic geometry, an analogue of a proper map for algebraic varieties * Proper transfer function, a transfer function in control theory in which the degree of the numerator does not exceed the degree of the denominator * Proper equilibrium, in game theory, a refinement of the Nash equilibrium * Proper subset * Proper space * Proper complex random variable Other uses * Proper (liturgy), the part of a Christian liturgy that is specific to the date within the Liturgical Year * Proper frame, such system of reference in which object is stationary (non moving), sometimes also called a co-moving frame * Proper (heraldry), in heraldry, means depicted in natural colors * Proper Records, a UK record label * Proper (album), an album by Into It. Over It. released in 2011 * Proper (often capitaliz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Map
In mathematics, a function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism. Definition There are several competing definitions of a "proper function". Some authors call a function f : X \to Y between two topological spaces if the preimage of every compact set in Y is compact in X. Other authors call a map f if it is continuous and ; that is if it is a continuous closed map and the preimage of every point in Y is compact. The two definitions are equivalent if Y is locally compact and Hausdorff. Let f : X \to Y be a closed map, such that f^(y) is compact (in X) for all y \in Y. Let K be a compact subset of Y. It remains to show that f^(K) is compact. Let \left\ be an open cover of f^(K). Then for all k \in K this is also an open cover of f^(k). Since the latter is assumed to be compact, it has a finite subcover. In other words, for every k \in K, there exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Morphism
In algebraic geometry, a proper morphism between schemes is an analog of a proper map between complex analytic spaces. Some authors call a proper variety over a field ''k'' a complete variety. For example, every projective variety over a field ''k'' is proper over ''k''. A scheme ''X'' of finite type over the complex numbers (for example, a variety) is proper over C if and only if the space ''X''(C) of complex points with the classical (Euclidean) topology is compact and Hausdorff. A closed immersion is proper. A morphism is finite if and only if it is proper and quasi-finite. Definition A morphism ''f'': ''X'' → ''Y'' of schemes is called universally closed if for every scheme ''Z'' with a morphism ''Z'' → ''Y'', the projection from the fiber product :X \times_Y Z \to Z is a closed map of the underlying topological spaces. A morphism of schemes is called proper if it is separated, of finite type, and universally closed ( GAII, 5.4.. One also says that ''X'' is proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Transfer Function
In control theory, a proper transfer function is a transfer function in which the degree Degree may refer to: As a unit of measurement * Degree (angle), a unit of angle measurement ** Degree of geographical latitude ** Degree of geographical longitude * Degree symbol (°), a notation used in science, engineering, and mathematics ... of the numerator does not exceed the degree of the denominator. A strictly proper transfer function is a transfer function where the degree of the numerator is less than the degree of the denominator. The difference between the degree of the denominator (number of poles) and degree of the numerator (number of zeros) is the ''relative degree'' of the transfer function. Example The following transfer function: : \textbf(s) = \frac = \frac is proper, because : \deg(\textbf(s)) = 4 \leq \deg(\textbf(s)) = 4 . is biproper, because : \deg(\textbf(s)) = 4 = \deg(\textbf(s)) = 4 . but is not strictly proper, because : \deg(\textbf(s)) = 4 \nless \deg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Equilibrium
Proper equilibrium is a refinement of Nash Equilibrium due to Roger B. Myerson. Proper equilibrium further refines Reinhard Selten's notion of a trembling hand perfect equilibrium by assuming that more costly trembles are made with significantly smaller probability than less costly ones. Definition Given a normal form game and a parameter \epsilon > 0, a totally mixed strategy profile \sigma is defined to be \epsilon-proper if, whenever a player has two pure strategies s and s' such that the expected payoff of playing s is smaller than the expected payoff of playing s' (that is u(s,\sigma_) Example The game to the right is a var ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Subset
In mathematics, set ''A'' is a subset of a set ''B'' if all elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra under the subset relation, in which the join and meet are given by intersection and union, and the subset relation itself is the Boolean inclusion relation. Definition If ''A'' and ''B'' are sets and every element of ''A'' is also an element of ''B'', then: :*''A'' is a subset of ''B'', denoted by A \subseteq B, or equivalently, :* ''B'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Space
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology. The following articles may also be useful; they either contain specialised vocabulary or provide more detailed expositions of the definitions given below. * Connection * Curvature * Metric space * Riemannian manifold See also: * Glossary of general topology * Glossary of differential geometry and topology * List of differential geometry topics Unless stated otherwise, letters ''X'', ''Y'', ''Z'' below denote metric spaces, ''M'', ''N'' denote Riemannian manifolds, , ''xy'', or , xy, _X denotes the distance between points ''x'' and ''y'' in ''X''. Italic ''word'' denotes a self-reference to this glossary. ''A caveat'': many terms in Riemannian and metric geometry, such as ''convex function'', ''convex set'' and others, do not have exactly the same meaning as in general mathematical usage. __NOTOC__ A Alexandrov space a gene ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
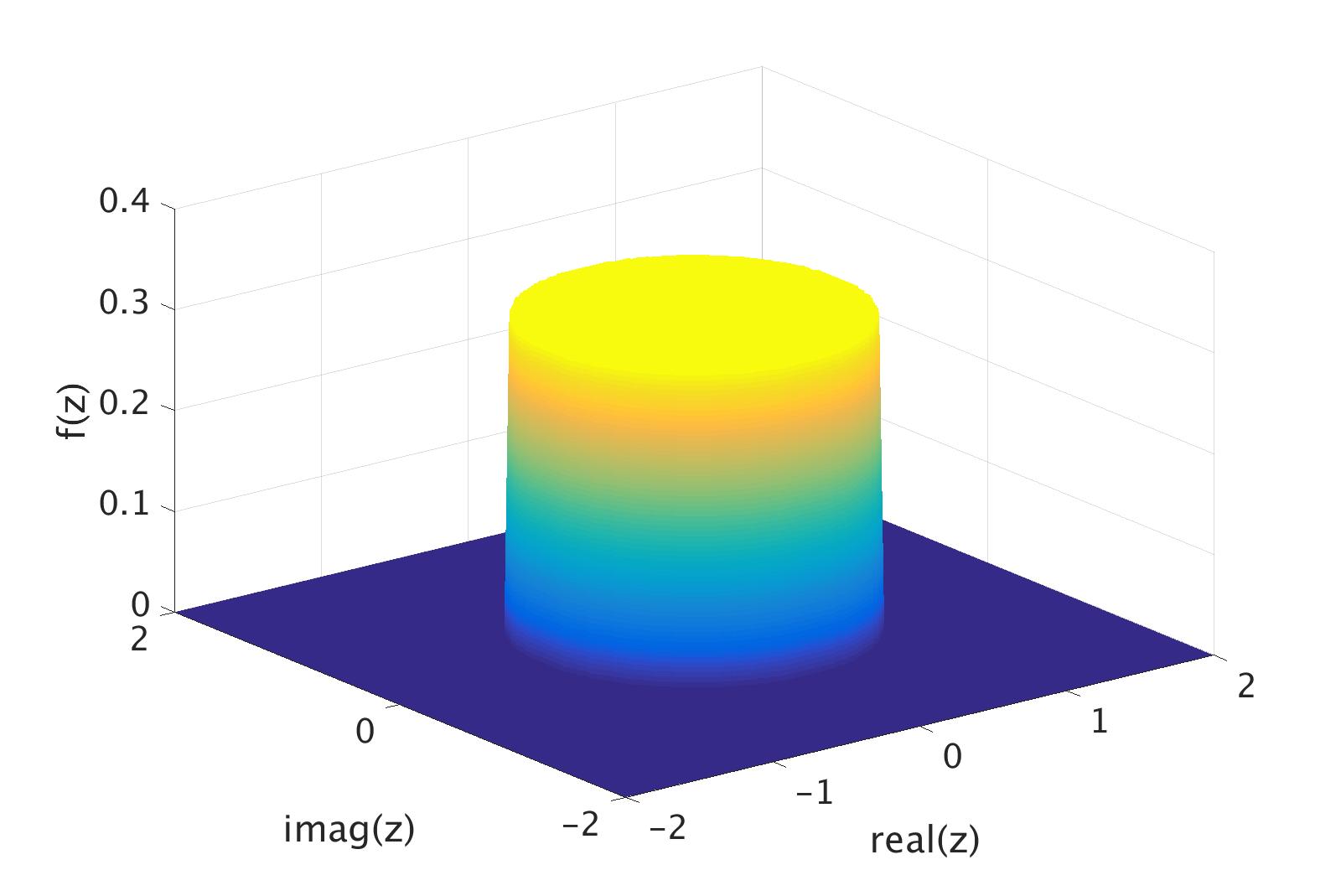
Complex Random Variable
In probability theory and statistics, complex random variables are a generalization of real-valued random variables to complex numbers, i.e. the possible values a complex random variable may take are complex numbers. Complex random variables can always be considered as pairs of real random variables: their real and imaginary parts. Therefore, the distribution of one complex random variable may be interpreted as the joint distribution of two real random variables. Some concepts of real random variables have a straightforward generalization to complex random variables—e.g., the definition of the mean of a complex random variable. Other concepts are unique to complex random variables. Applications of complex random variables are found in digital signal processing, quadrature amplitude modulation and information theory. Definition A complex random variable Z on the probability space (\Omega,\mathcal,P) is a function Z \colon \Omega \rightarrow \mathbb such that both its real part ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper (liturgy)
The proper (Latin: ''proprium'') is a part of the Christian liturgy that varies according to the date, either representing an observance within the liturgical year, or of a particular saint or significant event. The term is used in contrast to the '' ordinary'', which is that part of the liturgy that is reasonably constant, or at least selected without regard to date, or to the ''common'', which contains those parts of the liturgy that are common to an entire category of saints, such as apostles or martyrs. Propers may include hymns and prayers in the canonical hours and in the Eucharist. West The proper of the mass, strictly speaking, consists of the Introit, Gradual, Alleluia or Tract, Sequence, Offertory, and Communion - in other words, all the variable portions of a mass which are spoken or sung by the choir or the people. These are sometimes called the "minor propers" to distinguish them from the collect, secret, postcommunion, and readings - in other words, all the variab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Frame
A proper frame, or comoving frame, is a frame of reference that is attached to an object. The object in this frame is stationary within the frame, which is useful for many types of calculations. For example, a freely falling elevator is a proper frame for a free-falling object in the elevator, while the surface of the Earth is not. But, for an object on the Earth's surface, the Earth's surface is a proper frame while the falling elevator is not a proper frame. Proper frames can be inertial and non-inertial, as in the example above. The use of a proper frame is essential for the investigation of physical laws within the framework of general relativity. The term comoving frame is also a good description of a non-inertial frame, which is useful for many of the same uses as we mentioned previously. One advantage of proper frame and comoving frame is that the two frames must always maintain the same spatial position (i. "in the frame" - e.g. on the same frame of reference). This inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper (heraldry)
Tincture is the limited palette of colours and patterns used in heraldry. The need to define, depict, and correctly blazon the various tinctures is one of the most important aspects of heraldic art and design. Development and history The use of tinctures dates back to the formative period of European heraldry in the twelfth and thirteenth centuries. The range of tinctures and the manner of depicting and describing them has evolved over time, as new variations and practices have developed. The basic scheme and rules of applying the heraldic tinctures dates back to the 12th century. The earliest surviving coloured heraldic illustrations, from the mid-thirteenth century, show the standardized usage of two metals, five colours, and two furs. Since that time, the great majority of heraldic art has employed these nine tinctures. Over time, variations on these basic tinctures were developed, particularly with respect to the furs. Authorities differ as to whether these variations shou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper Records
Proper Records is an English record label founded by Proper Music Group Chairman - Malcolm Mills and Paul Riley. Commencing with a handful of releases, including the Balham Alligators and Chilli Willi and the Red Hot Peppers, the label grew in stature and renown through its reissue marque, 'Proper Box'. Featuring jazz, country, and rock and roll artists, these releases now total over 200. The label has become better known for releasing new albums by contemporary artists such as Bonnie Raitt, Joan Baez, Richard Thompson, Nick Lowe, Dr. John, Los Lobos, Willie Nelson & Asleep At The Wheel, The Blind Boys Of Alabama, Loudon Wainwright III and many more. Subsidiary labels include Specific Jazz and Navigator Records. The company was based on an industrial estate in south London but relocated to Surrey Quays in 2017. Sister company Proper Music Distribution has won the ''Music Week'' Distributor of the Year Award three times. Roster * Aimee Mann * Alison Moorer * Andy Fairweather ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proper (album)
Into It. Over It. is the indie rock solo project of the Chicago, Illinois-based musician Evan Thomas Weiss. It is considered one of the top acts in the emo revival scene of the 2010s. History Evan Weiss grew up in Cherry Hill, New Jersey. His first exposure to emo was hearing the band Sunny Day Real Estate in the seventh grade while browsing a record shop. He continued his interest in music by buying Jade Tree and Polyvinyl recordings and going to local shows in Philadelphia. In the fourth or fifth grade, Weiss started the band J.A.R. with school friends; it eventually became The Progress and garnered modest local success. The Progress released an album and two EPs before breaking up in 2008. The Progress later reunited sporadically to perform one-off live shows. However, Weiss could not convince his bandmates to play in the band full-time. Weiss started a solo project under the moniker ''Into It. Over It.'' He first released music through two unorthodox concept projects: ''52 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |