|
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Line
In mathematics, a projective line is, roughly speaking, the extension of a usual line by a point called a ''point at infinity''. The statement and the proof of many theorems of geometry are simplified by the resultant elimination of special cases; for example, two distinct projective lines in a projective plane meet in exactly one point (there is no "parallel" case). There are many equivalent ways to formally define a projective line; one of the most common is to define a projective line over a field ''K'', commonly denoted P1(''K''), as the set of one-dimensional subspaces of a two-dimensional ''K''-vector space. This definition is a special instance of the general definition of a projective space. The projective line over the reals is a manifold; see real projective line for details. Homogeneous coordinates An arbitrary point in the projective line P1(''K'') may be represented by an equivalence class of ''homogeneous coordinates'', which take the form of a pair : _1 : x_2/ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coplanar Lines
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. However, a set of four or more distinct points will, in general, not lie in a single plane. Two lines in three-dimensional space are coplanar if there is a plane that includes them both. This occurs if the lines are parallel, or if they intersect each other. Two lines that are not coplanar are called skew lines. Distance geometry provides a solution technique for the problem of determining whether a set of points is coplanar, knowing only the distances between them. Properties in three dimensions In three-dimensional space, two linearly independent vectors with the same initial point determine a plane through that point. Their cross product is a normal vector to that plane, and any vector orthogonal to this cross product through the initi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Space R3
Affine may describe any of various topics concerned with connections or affinities. It may refer to: * Affine, a relative by marriage in law and anthropology * Affine cipher, a special case of the more general substitution cipher * Affine combination, a certain kind of constrained linear combination * Affine connection, a connection on the tangent bundle of a differentiable manifold * Affine Coordinate System, a coordinate system that can be viewed as a Cartesian coordinate system where the axes have been placed so that they are not necessarily orthogonal to each other. See tensor. * Affine differential geometry, a geometry that studies differential invariants under the action of the special affine group * Affine gap penalty, the most widely used scoring function used for sequence alignment, especially in bioinformatics * Affine geometry, a geometry characterized by parallel lines * Affine group, the group of all invertible affine transformations from any affine space over a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-orientable Manifold
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is orientable if such a consistent definition exists. In this case, there are two possible definitions, and a choice between them is an orientation of the space. Real vector spaces, Euclidean spaces, and spheres are orientable. A space is non-orientable if "clockwise" is changed into "counterclockwise" after running through some loops in it, and coming back to the starting point. This means that a geometric shape, such as , that moves continuously along such a loop is changed into its own mirror image . A Möbius strip is an example of a non-orientable space. Various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifold ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold Theory
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a '' topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity e, a number ranging from e = 0 (the limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution. Analytically, the equation of a standard ellipse centered at the origin with width 2a and height 2b is: : \frac+\frac = 1 . Assuming a \ge b, the foci are (\pm c, 0) for c = \sqrt. The standard parametric equation is: : (x,y) = (a\cos(t),b\sin(t)) \quad \text \quad 0\leq t\leq 2\pi. Ellipses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Hyperbolas arise in many ways: * as the curve representing the reciprocal function y(x) = 1/x in the Cartesian plane, * as the path followed by the shadow of the tip of a sundial, * as the shape of an open orbit (as distinct from a closed elliptical orbit), such as the orbit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
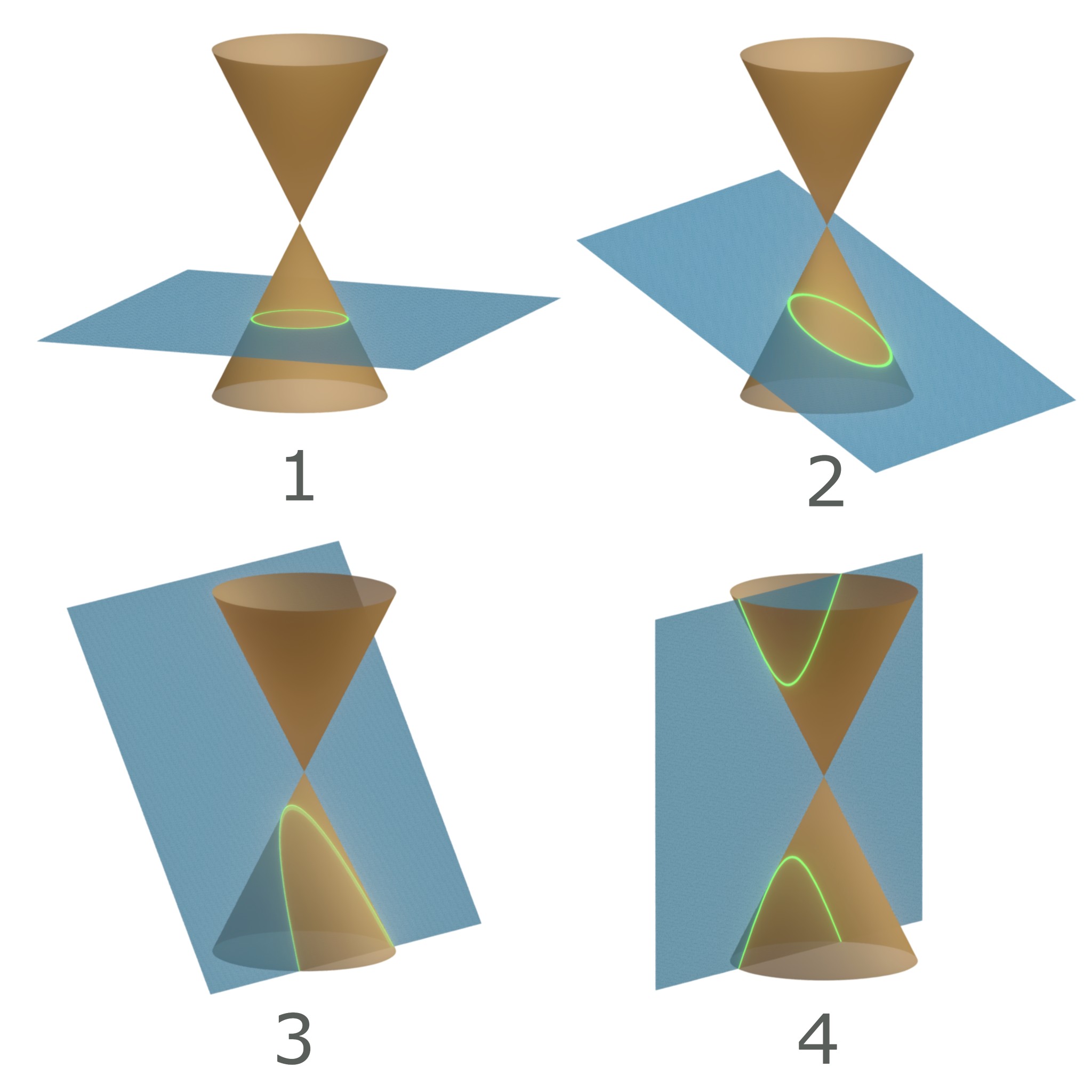
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called " points at infinity") to Euclidean points, and vice-versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. It is not possible to refer to angles in projective geometry as it is in Euclidean geometry, because a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |