|
Planetary Boundary Layer
In meteorology, the planetary boundary layer (PBL), also known as the atmospheric boundary layer (ABL) or peplosphere, is the lowest part of the atmosphere and its behaviour is directly influenced by its contact with a planetary surface. On Earth it usually responds to changes in surface radiative forcing in an hour or less. In this layer physical quantities such as flow velocity, temperature, and moisture display rapid fluctuations (turbulence) and vertical mixing is strong. Above the PBL is the "free atmosphere", where the wind is approximately geostrophic (parallel to the isobars), while within the PBL the wind is affected by surface drag and turns across the isobars (see Ekman layer for more detail). Cause of surface wind gradient Typically, due to aerodynamic drag, there is a wind gradient in the wind flow ~100 meters above the Earth's surface—the surface layer of the planetary boundary layer. Wind speed increases with increasing height above the ground, starting f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Air Over Los Angeles
''The'' () is a grammatical article in English, denoting persons or things already mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with pronouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of pronoun '' thee'') when followed by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixing (physics)
In physics, a dynamical system is said to be mixing if the phase space of the system becomes strongly intertwined, according to at least one of several mathematical definitions. For example, a measure-preserving transformation ''T'' is said to be strong mixing if : \lim_ \, \mu(T^A \cap B) = \mu(A) \cdot \mu(B) whenever ''A'' and ''B'' are any measurable sets and μ is the associated measure. Other definitions are possible, including weak mixing and topological mixing. The mathematical definition of mixing is meant to capture the notion of physical mixing. A canonical example is the Cuba libre: suppose one is adding rum (the set ''A'') to a glass of cola. After stirring the glass, the bottom half of the glass (the set ''B'') will contain rum, and it will be in equal proportion as it is elsewhere in the glass. The mixing is uniform: no matter which region ''B'' one looks at, some of ''A'' will be in that region. A far more detailed, but still informal description of mixin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
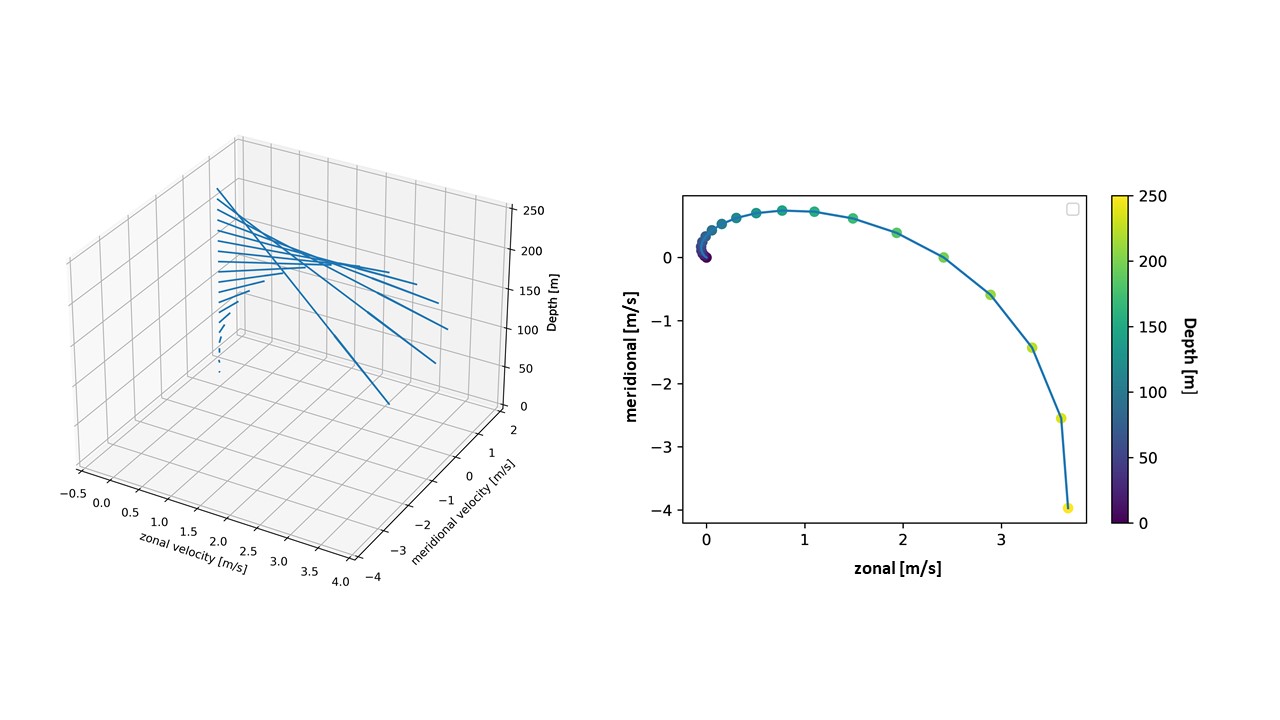
Ekman Spiral
The oceanic, wind driven Ekman spiral is the result of a force balance created by a shear stress force, Coriolis force and the water drag. This force balance gives a resulting current of the water different from the winds. In the ocean, there are two places where the Ekman spiral can be observed. At the surface of the ocean, the shear stress force corresponds with the wind stress force. At the bottom of the ocean, the shear stress force is created by friction with the ocean floor. This phenomenon was first observed at the surface by the Norwegian oceanographer Fridtjof Nansen during his Fram expedition. He noticed that icebergs did not drift in the same direction as the wind. His student, the Swedish oceanographer Vagn Walfrid Ekman, was the first person to physically explain this process. Bottom Ekman Spiral In order to derive the properties of an Ekman spiral a look is taken at a uniform, horizontal geostrophic interior flow in a homogeneous fluid. This flow will by denoted by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shearing (physics)
In continuum mechanics, shearing refers to the occurrence of a shear strain, which is a deformation of a material substance in which parallel internal surfaces slide past one another. It is induced by a shear stress in the material. Shear strain is distinguished from volumetric strain. The change in a material's volume in response to stress and change of angle is called the angle of shear. Overview Often, the verb ''shearing'' refers more specifically to a mechanical process that causes a plastic shear strain in a material, rather than causing a merely elastic one. A plastic shear strain is a continuous (non-fracturing) deformation that is irreversible, such that the material does not recover its original shape. It occurs when the material is yielding. The process of shearing a material may induce a volumetric strain along with the shear strain. In soil mechanics, the volumetric strain associated with shearing is known as Reynolds' dilation if it increases the volume, or c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Meteorological Society
The American Meteorological Society (AMS) is the premier scientific and professional organization in the United States promoting and disseminating information about the Atmospheric sciences, atmospheric, Oceanography, oceanic, and Hydrology, hydrologic sciences. Its mission is to advance the atmospheric and related sciences, technologies, applications, and services for the benefit of society. Background Founded on December 29, 1919, by Charles Franklin Brooks at a meeting of the American Association for the Advancement of Science in St. Louis and incorporated on January 21, 1920, the American Meteorological Society has a membership of more than 13,000 weather, water, and climate scientists, professionals, researchers, educators, students, and enthusiasts. AMS offers numerous programs and services in the sphere of water, weather and climate sciences. It publishes eleven atmospheric and related oceanic and hydrologic journals (in print and online), sponsors as many as twelve conf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Applied Meteorology
The ''Journal of Applied Meteorology and Climatology'' (JAMC; formerly ''Journal of Applied Meteorology'') is a scientific journal published by the American Meteorological Society. Applied research related to the physical meteorology, cloud physics, hydrology, weather modification, satellite meteorology, boundary layer processes, air pollution meteorology (including dispersion and chemical processes), agricultural and forest meteorology, and applied meteorological numerical models of all types. See also * List of scientific journals ** List of scientific journals in earth and atmospheric sciences A ''list'' is any set of items in a row. List or lists may also refer to: People * List (surname) Organizations * List College, an undergraduate division of the Jewish Theological Seminary of America * SC Germania List, German rugby union ... Atmospheric dispersion modeling Publications established in 1962 English-language journals American Meteorological Society academ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log Wind Profile
The log wind profile is a semi-empirical relationship commonly used to describe the vertical distribution of horizontal mean wind speeds within the lowest portion of the planetary boundary layer. The relationship is well described in the literature. The logarithmic profile of wind speeds is generally limited to the lowest 100 m of the atmosphere (i.e., the surface layer of the atmospheric boundary layer). The rest of the atmosphere is composed of the remaining part of the planetary boundary layer (up to around 1000 m) and the troposphere or free atmosphere. In the free atmosphere, geostrophic wind relationships should be used. Definition The equation to estimate the mean wind speed (u_z) at height z (meters) above the ground is: where u_* is the friction velocity (m s−1), \kappa is the Von Kármán constant (~0.41), d is the zero plane displacement (in metres), z_0 is the surface roughness (in meters), and \psi is a stability term where L is the Obukhov length from Monin- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of is , or . The logarithm of to ''base'' is denoted as , or without parentheses, , or even without the explicit base, , when no confusion is possible, or when the base does not matter such as in big O notation. The logarithm base is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number as its base; its use is widespread in mathematics and physics, because of its very simple derivative. The binary logarithm uses base and is frequently used in computer science. Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. They were rapidly adopted by navigators, scientists, engineers, surveyors and others to perform high-a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponent
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\ ex& = \underbrace_ \times \underbrace_ \\ ex& = b^n \times b^m \end In other words, when multiplying a base raised to one exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a Exponentiation, power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four. Empirical examples The distributions of a wide variety of physical, biological, and man-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the species richness in clades of organisms, the sizes of power outages, volcanic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Simple Shear
Simple shear is a deformation in which parallel planes in a material remain parallel and maintain a constant distance, while translating relative to each other. In fluid mechanics In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value: :V_x=f(x,y) :V_y=V_z=0 And the gradient of velocity is constant and perpendicular to the velocity itself: :\frac = \dot \gamma , where \dot \gamma is the shear rate and: :\frac = \frac = 0 The displacement gradient tensor Γ for this deformation has only one nonzero term: :\Gamma = \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end Simple shear with the rate \dot \gamma is the combination of pure shear strain with the rate of \dot \gamma and rotation with the rate of \dot \gamma: :\Gamma = \begin \underbrace \begin 0 & & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox\end = \begin \underbrace \begin 0 & & 0 \\ & 0 & 0 \\ 0 & 0 & 0 \end \\ \mbox \end + \begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more specialized List of engineering branches, fields of engineering, each with a more specific emphasis on particular areas of applied mathematics, applied science, and types of application. See glossary of engineering. The term ''engineering'' is derived from the Latin ''ingenium'', meaning "cleverness" and ''ingeniare'', meaning "to contrive, devise". Definition The American Engineers' Council for Professional Development (ECPD, the predecessor of Accreditation Board for Engineering and Technology, ABET) has defined "engineering" as: The creative application of scientific principles to design or develop structures, machines, apparatus, or manufacturing processes, or works utilizing them singly or in combination; or to construct o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.png)