|
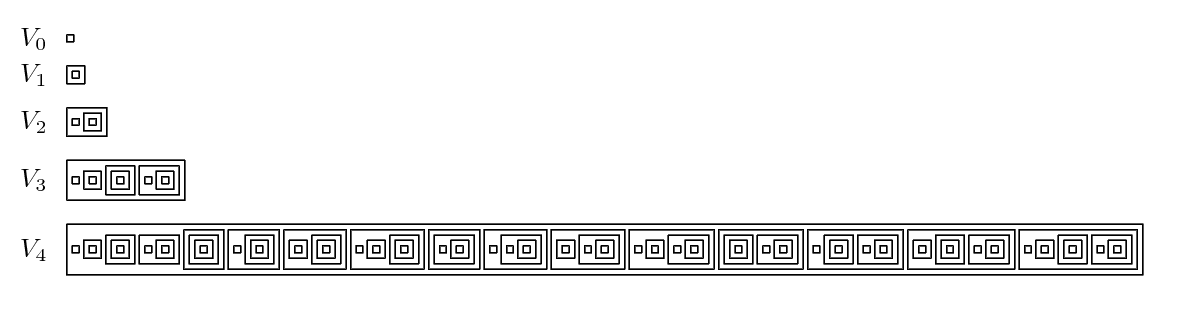
Pure Set
In set theory, a hereditary set (or pure set) is a set whose elements are all hereditary sets. That is, all elements of the set are themselves sets, as are all elements of the elements, and so on. Examples For example, it is vacuously true that the empty set is a hereditary set, and thus the set \ containing only the empty set \varnothing is a hereditary set. Similarly, a set \ that contains two elements: the empty set and the set that contains only the empty set, is a hereditary set. In formulations of set theory In formulations of set theory that are intended to be interpreted in the von Neumann universe or to express the content of Zermelo–Fraenkel set theory, ''all'' sets are hereditary, because the only sort of object that is even a candidate to be an element of a set is another set. Thus the notion of hereditary set is interesting only in a context in which there may be urelements. Assumptions The inductive definition of hereditary sets presupposes that set membership ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Set Theory
Set theory is the branch of mathematical logic that studies Set (mathematics), sets, which can be informally described as collections of objects. Although objects of any kind can be collected into a set, set theory – as a branch of mathematics – is mostly concerned with those that are relevant to mathematics as a whole. The modern study of set theory was initiated by the German mathematicians Richard Dedekind and Georg Cantor in the 1870s. In particular, Georg Cantor is commonly considered the founder of set theory. The non-formalized systems investigated during this early stage go under the name of ''naive set theory''. After the discovery of Paradoxes of set theory, paradoxes within naive set theory (such as Russell's paradox, Cantor's paradox and the Burali-Forti paradox), various axiomatic systems were proposed in the early twentieth century, of which Zermelo–Fraenkel set theory (with or without the axiom of choice) is still the best-known and most studied. Set the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Vacuously True
In mathematics and logic, a vacuous truth is a conditional or universal statement (a universal statement that can be converted to a conditional statement) that is true because the antecedent cannot be satisfied. It is sometimes said that a statement is vacuously true because it does not really say anything. For example, the statement "all cell phones in the room are turned off" will be true when no cell phones are present in the room. In this case, the statement "all cell phones in the room are turned ''on''" would also be vacuously true, as would the conjunction of the two: "all cell phones in the room are turned on ''and'' turned off", which would otherwise be incoherent and false. More formally, a relatively well-defined usage refers to a conditional statement (or a universal conditional statement) with a false antecedent. One example of such a statement is "if Tokyo is in Spain, then the Eiffel Tower is in Bolivia". Such statements are considered vacuous truths because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Empty Set
In mathematics, the empty set or void set is the unique Set (mathematics), set having no Element (mathematics), elements; its size or cardinality (count of elements in a set) is 0, zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set. Any set other than the empty set is called ''non-empty''. In some textbooks and popularizations, the empty set is referred to as the "null set". However, null set is a distinct notion within the context of measure theory, in which it describes a set of measure zero (which is not necessarily empty). Notation Common notations for the empty set include "", "\emptyset", and "∅". The latter two symbols were introduced by the Bourbaki group (specifically André Weil) in 1939, inspired by the letter Ø () in the Danish orthography, Danish and Norwegian orthography, Norwegian a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Von Neumann Universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Zermelo–Fraenkel Set Theory
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded. Informally, Zermelo–Fraenkel set theory is intended to formalize a single primitive notion, that of a hereditary well-founded set, so that all entities in the universe of discourse are such sets. Thus the axioms of Zermelo–Fraenkel set theory refer only to pure sets and prevent its models fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Urelement
In set theory, a branch of mathematics, an urelement or ur-element (from the German prefix ''ur-'', 'primordial') is an object that is not a set (has no elements), but that may be an element of a set. It is also referred to as an atom or individual. Ur-elements are also not identical with the empty set. Theory There are several different but essentially equivalent ways to treat urelements in a first-order theory. One way is to work in a first-order theory with two sorts, sets and urelements, with ''a'' ∈ ''b'' only defined when ''b'' is a set. In this case, if ''U'' is an urelement, it makes no sense to say X \in U, although U \in X is perfectly legitimate. Another way is to work in a one-sorted theory with a unary relation used to distinguish sets and urelements. As non-empty sets contain members while urelements do not, the unary relation is only needed to distinguish the empty set from urelements. Note that in this case, the axiom of extensionality must be formulated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Well-founded Relation
In mathematics, a binary relation is called well-founded (or wellfounded or foundational) on a set or, more generally, a class if every non-empty subset has a minimal element with respect to ; that is, there exists an such that, for every , one does not have . In other words, a relation is well-founded if: (\forall S \subseteq X)\; \neq \varnothing \implies (\exists m \in S) (\forall s \in S) \lnot(s \mathrel m) Some authors include an extra condition that is set-like, i.e., that the elements less than any given element form a set. Equivalently, assuming the axiom of dependent choice, a relation is well-founded when it contains no infinite descending chains, meaning there is no infinite sequence of elements of such that for every natural number . In order theory, a partial order is called well-founded if the corresponding strict order is a well-founded relation. If the order is a total order then it is called a well-order. In set theory, a set is called a well-fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Axiom Of Regularity
In mathematics, the axiom of regularity (also known as the axiom of foundation) is an axiom of Zermelo–Fraenkel set theory that states that every Empty set, non-empty Set (mathematics), set ''A'' contains an element that is Disjoint sets, disjoint from ''A''. In first-order logic, the axiom reads: \forall x\,(x \neq \varnothing \rightarrow (\exists y \in x) (y \cap x = \varnothing)). The axiom of regularity together with the axiom of pairing implies that Russell paradox, no set is an element of itself, and that there is no infinite sequence (a_n) such that a_ is an element of a_i for all i. With the axiom of dependent choice (which is a weakened form of the axiom of choice), this result can be reversed: if there are no such infinite sequences, then the axiom of regularity is true. Hence, in this context the axiom of regularity is equivalent to the sentence that there are no downward infinite membership chains. The axiom was originally formulated by von Neumann; it was adopted in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Transitive Set
In set theory, a branch of mathematics, a set A is called transitive if either of the following equivalent conditions holds: * whenever x \in A, and y \in x, then y \in A. * whenever x \in A, and x is not an urelement, then x is a subset of A. Similarly, a class M is transitive if every element of M is a subset of M. Examples Using the definition of ordinal numbers suggested by John von Neumann, ordinal numbers are defined as hereditarily transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals). The class of all ordinals is a transitive class. Any of the stages V_\alpha and L_\alpha leading to the construction of the von Neumann universe V and Gödel's constructible universe L are transitive sets. The universes V and L themselves are transitive classes. This is a complete list of all finite transitive sets with up to 20 brackets: * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \, * \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Non-well-founded Set Theories
Non-well-founded set theories are variants of axiomatic set theory that allow sets to be elements of themselves and otherwise violate the rule of well-foundedness. In non-well-founded set theories, the foundation axiom of ZFC is replaced by axioms implying its negation. The study of non-well-founded sets was initiated by Dmitry Mirimanoff in a series of papers between 1917 and 1920, in which he formulated the distinction between well-founded and non-well-founded sets; he did not regard well-foundedness as an axiom. Although a number of axiomatic systems of non-well-founded sets were proposed afterwards, they did not find much in the way of applications until the book Non-Well-Founded Sets by Peter Aczel introduces hyperset theory in 1988. The theory of non-well-founded sets has been applied in the logical modelling of non-terminating computational processes in computer science (process algebra and final semantics), linguistics and natural language semantics (situation theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hereditarily Countable Set
In set theory, a set is called hereditarily countable if it is a countable set of hereditarily countable sets. Results The inductive definition above is well-founded and can be expressed in the language of first-order set theory. Equivalent properties A set is hereditarily countable if and only if it is countable, and every element of its transitive closure is countable. by . See also * * |