|
Probability Management
The discipline of probability management communicates and calculates uncertainties as data structures that obey both the laws of arithmetic and probability, while preserving statistical coherence. The simplest approach is to use vector arrays of simulated or historical realizations and metadata called Stochastic Information Packets (SIPs). A set of SIPs, which preserve statistical relationships between variables, is said to be coherent and is referred to as a Stochastic Library Unit with Relationships Preserved (SLURP). SIPs and SLURPs allow stochastic simulations to communicate with one another. For example, see Analytica (Wikipedia), AnalyticaSIP page an Autobox The first large documented application of SIPs involved the explo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytica (software)
Analytica is a visual software developed by Lumina Decision Systems for creating, analyzing and communicating quantitative decision models. It combines hierarchical influence diagrams for visual creation and view of models, intelligent arrays for working with multidimensional data, Monte Carlo simulation for analyzing risk and uncertainty, and optimization, including linear and nonlinear programming. Its design, especially its influence diagrams and treatment of uncertainty, is based on ideas from the field of decision analysis. As a computer language, it combines a declarative (non-procedural) structure for referential transparency, array abstraction, and automatic dependency maintenance for efficient sequencing of computation. Hierarchical influence diagrams Analytica models are organized as influence diagrams. Variables (and other objects) appear as nodes of various shapes on a diagram, connected by arrows that provide a visual representation of dependencies. Analytica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrew Gelman
Andrew Eric Gelman (born February 11, 1965) is an American statistician and professor of statistics and political science at Columbia University. Gelman received bachelor of science degrees in mathematics and in physics from MIT, where he was a National Merit Scholar, in 1986. He then received a master of science in 1987 and a doctor of philosophy in 1990, both in statistics from Harvard University, under the supervision of Donald Rubin. Career Gelman is the Higgins Professor of Statistics and Professor of Political Science and the Director of the Applied Statistics Center at Columbia University. He is a major contributor to statistical philosophy and methods especially in Bayesian statistics and hierarchical models. He is one of the leaders of the development of the statistical programming framework Stan. Perspective on Statistical Inference and Hypothesis Testing Gelman's approach to statistical inference emphasizes studying variation and the associations between data, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
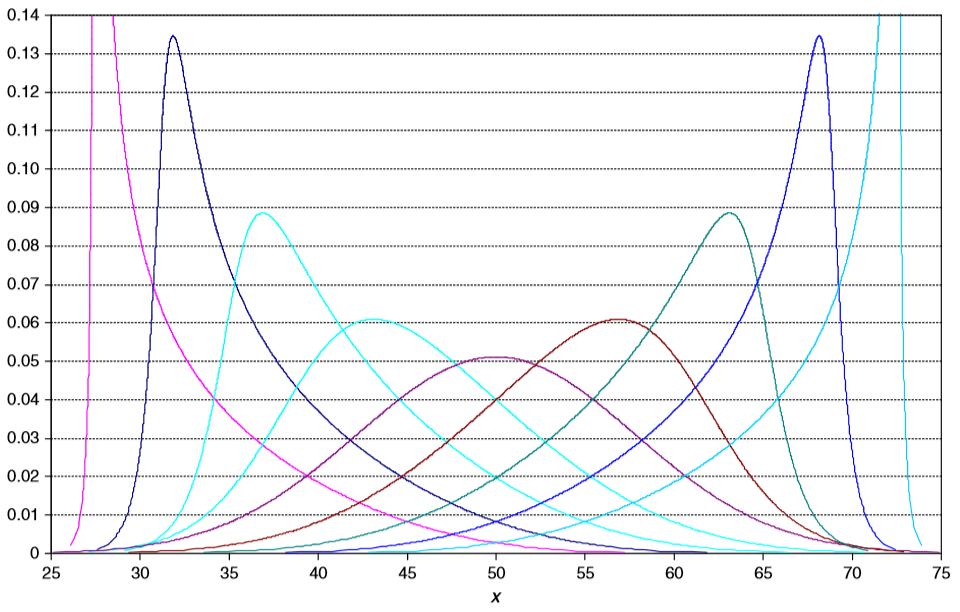
Metalog Distribution
The metalog distribution is a flexible continuous probability distribution designed for ease of use in practice. Together with its transforms, the metalog family of continuous distributions is unique because it embodies ''all'' of following properties: virtually unlimited shape flexibility; a choice among unbounded, semi-bounded, and bounded distributions; ease of fitting to data with linear least squares; simple, closed-form quantile function (inverse CDF) equations that facilitate simulation; a simple, closed-form PDF; and Bayesian updating in closed form in light of new data. Moreover, like a Taylor series, metalog distributions may have any number of terms, depending on the degree of shape flexibility desired and other application needs. Applications where metalog distributions can be useful typically involve fitting empirical data, simulated data, or expert-elicited quantiles to smooth, continuous probability distributions. Fields of application are wide-ranging, and include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Douglas W
Douglas may refer to: People * Douglas (given name) * Douglas (surname) Animals * Douglas (parrot), macaw that starred as the parrot ''Rosalinda'' in Pippi Longstocking * Douglas the camel, a camel in the Confederate Army in the American Civil War Businesses * Douglas Aircraft Company * Douglas (cosmetics), German cosmetics retail chain in Europe * Douglas (motorcycles), British motorcycle manufacturer Peerage and Baronetage * Duke of Douglas * Earl of Douglas, or any holder of the title * Marquess of Douglas, or any holder of the title * Douglas Baronets Peoples * Clan Douglas, a Scottish kindred * Dougla people, West Indians of both African and East Indian heritage Places Australia * Douglas, Queensland, a suburb of Townsville * Douglas, Queensland (Toowoomba Region), a locality * Port Douglas, North Queensland, Australia * Shire of Douglas, in northern Queensland Belize * Douglas, Belize Canada * Douglas, New Brunswick * Douglas Parish, New Brunswick ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harry Markowitz
Harry Max Markowitz (born August 24, 1927) is an American economist who received the 1989 John von Neumann Theory Prize and the 1990 Nobel Memorial Prize in Economic Sciences. Markowitz is a professor of finance at the Rady School of Management at the University of California, San Diego (UCSD). He is best known for his pioneering work in modern portfolio theory, studying the effects of asset risk, return, correlation and diversification on probable investment portfolio returns. Biography Harry Markowitz was born to a Jewish family, the son of Morris and Mildred Markowitz.Harry M. Markowitz �Autobiography The Nobel Prizes 1990, Editor Tore Frängsmyr, obel Foundation Stockholm, 1991 During high school, Markowitz developed an interest in physics and philosophy, in particular the ideas of David Hume, an interest he continued to follow during his undergraduate years at the University of Chicago. After receiving his Ph.B. in Liberal Arts, Markowitz decided to continue his ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Simulation
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.DLOUHÝ, M.; FÁBRY, J.; KUNCOVÁ, M.. Simulace pro ekonomy. Praha : VŠE, 2005. Realizations of these random variables are generated and inserted into a model of the system. Outputs of the model are recorded, and then the process is repeated with a new set of random values. These steps are repeated until a sufficient amount of data is gathered. In the end, the distribution of the outputs shows the most probable estimates as well as a frame of expectations regarding what ranges of values the variables are more or less likely to fall in. Often random variables inserted into the model are created on a computer with a random number generator (RNG). The U(0,1) uniform distribution outputs of the random number generator are then transformed into random variables with probability distributions that are used in the system model. Etymology ''Stoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Methods
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distributions
In probability theory and statistics, a probability distribution is the mathematical Function (mathematics), function that gives the probabilities of occurrence of different possible outcomes for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a Survey methodology, survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |