|
Prediction Error
In statistics the mean squared prediction error (MSPE), also known as mean squared error of the predictions, of a smoothing, curve fitting, or regression procedure is the expected value of the squared prediction errors (PE), the square difference between the fitted values implied by the predictive function \widehat and the values of the (unobservable) true value ''g''. It is an inverse measure of the ''explanatory power'' of \widehat, and can be used in the process of cross-validation of an estimated model. Knowledge of ''g'' would be required in order to calculate the MSPE exactly; in practice, MSPE is estimated. Formulation If the smoothing or fitting procedure has projection matrix (i.e., hat matrix) ''L'', which maps the observed values vector y to predicted values vector \hat=Ly, then PE and MSPE are formulated as: :\operatorname=g(x_i)-\widehat(x_i), :\operatorname=\operatorname\left operatorname_i^2\right\sum_^n \operatorname_i^2/n. The MSPE can be decomposed into two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Data Analyst
Data analysis is the process of inspecting, cleansing, transforming, and modeling data with the goal of discovering useful information, informing conclusions, and supporting decision-making. Data analysis has multiple facets and approaches, encompassing diverse techniques under a variety of names, and is used in different business, science, and social science domains. In today's business world, data analysis plays a role in making decisions more scientific and helping businesses operate more effectively. Data mining is a particular data analysis technique that focuses on statistical modeling and knowledge discovery for predictive rather than purely descriptive purposes, while business intelligence covers data analysis that relies heavily on aggregation, focusing mainly on business information. In statistical applications, data analysis can be divided into descriptive statistics, exploratory data analysis (EDA), and confirmatory data analysis (CDA). EDA focuses on discovering ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Point Estimation Performance
A point is a small dot or the sharp tip of something. Point or points may refer to: Mathematics * Point (geometry), an entity that has a location in space or on a plane, but has no extent; more generally, an element of some abstract topological space * Point, or Element (category theory), generalizes the set-theoretic concept of an element of a set to an object of any category * Critical point (mathematics), a stationary point of a function of an arbitrary number of variables * Decimal point * Point-free geometry * Stationary point, a point in the domain of a single-valued function where the value of the function ceases to change Places * Point, Cornwall, England, a settlement in Feock parish * Point, Lewis, a peninsula in the Outer Hebrides, Scotland * Point, Texas, a city in Rains County, Texas, United States * Point, the NE tip and a ferry terminal of Lismore, Inner Hebrides, Scotland * Points, West Virginia, an unincorporated community in the United States Business an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
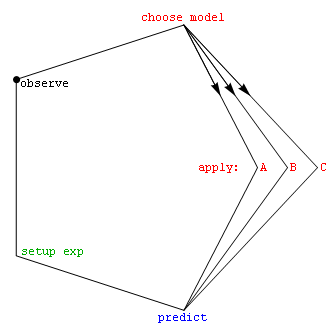
Model Selection
Model selection is the task of selecting a model from among various candidates on the basis of performance criterion to choose the best one. In the context of machine learning and more generally statistical analysis, this may be the selection of a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered. However, the task can also involve the design of experiments such that the data collected is well-suited to the problem of model selection. Given candidate models of similar predictive or explanatory power, the simplest model is most likely to be the best choice (Occam's razor). state, "The majority of the problems in statistical inference can be considered to be problems related to statistical modeling". Relatedly, has said, "How hetranslation from subject-matter problem to statistical model is done is often the most critical part of an analysis". Model selection may also refer to the problem of selecting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Law Of Total Variance
The law of total variance is a fundamental result in probability theory that expresses the variance of a random variable in terms of its conditional variances and conditional means given another random variable . Informally, it states that the overall variability of can be split into an “unexplained” component (the average of within-group variances) and an “explained” component (the variance of group means). Formally, if and are random variables on the same probability space, and has finite variance, then: \operatorname(Y) \;=\; \operatorname\bigl operatorname(Y \mid X)\bigr\;+\; \operatorname\!\bigl(\operatorname \mid Xbigr).\! This identity is also known as the variance decomposition formula, the conditional variance formula, the law of iterated variances, or colloquially as Eve’s law, in parallel to the “Adam’s law” naming for the law of total expectation. In actuarial science (particularly in credibility theory), the two terms \operatorname operatorna ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Errors And Residuals In Statistics
In statistics and optimization, errors and residuals are two closely related and easily confused measures of the deviation of an observed value of an element of a statistical sample from its "true value" (not necessarily observable). The error of an observation is the deviation of the observed value from the true value of a quantity of interest (for example, a population mean). The residual is the difference between the observed value and the '' estimated'' value of the quantity of interest (for example, a sample mean). The distinction is most important in regression analysis, where the concepts are sometimes called the regression errors and regression residuals and where they lead to the concept of studentized residuals. In econometrics, "errors" are also called disturbances. Introduction Suppose there is a series of observations from a univariate distribution and we want to estimate the mean of that distribution (the so-called location model). In this case, the errors a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mean Squared Error
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the true value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate. In machine learning, specifically empirical risk minimization, MSE may refer to the ''empirical'' risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution). The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the erro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Akaike Information Criterion
The Akaike information criterion (AIC) is an estimator of prediction error and thereby relative quality of statistical models for a given set of data. Given a collection of models for the data, AIC estimates the quality of each model, relative to each of the other models. Thus, AIC provides a means for model selection. AIC is founded on information theory. When a statistical model is used to represent the process that generated the data, the representation will almost never be exact; so some information will be lost by using the model to represent the process. AIC estimates the relative amount of information lost by a given model: the less information a model loses, the higher the quality of that model. In estimating the amount of information lost by a model, AIC deals with the trade-off between the goodness of fit of the model and the simplicity of the model. In other words, AIC deals with both the risk of overfitting and the risk of underfitting. The Akaike information crite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mallows's Cp
In statistics, Mallows's \boldsymbol, named for Colin Lingwood Mallows, is used to assess the goodness of fit, fit of a regression analysis, regression model that has been estimated using ordinary least squares. It is applied in the context of model selection, where a number of dependent and independent variables, predictor variables are available for predicting some outcome, and the goal is to find the best model involving a subset of these predictors. A small value of C_p means that the model is relatively precise. Mallows's ''Cp'' is ’essentially equivalent‘ to the Akaike Information Criterion in the case of linear regression. This equivalence is only asymptotic; Akaike notes that ''Cp'' requires some subjective judgment in the choice of \hat\sigma^2. Definition and properties Mallows's ''Cp'' addresses the issue of overfitting, in which model selection statistics such as the residual sum of squares always get smaller as more variables are added to a model. Thus, if we aim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Colin Mallows
Colin Lingwood Mallows (10 September 1930 – 4 November 2023) was an English statistician, who worked in the United States from 1960. He was known for Mallows's ''Cp'', a regression model diagnostic procedure, widely used in regression analysis and the Fowlkes–Mallows index, a popular clustering validation criterion. Education and career Mallows began studying at University College London (UCL) in 1948 and received in 1951 his bachelor's degree and in 1953 his PhD (at the age of 22) from under Florence Nightingale David and Norman Lloyd Johnson with thesis ''Some problems connected with distribution problems.'' Mallows joined the UCL faculty and taught there from 1955 to 1959 with a sabbatical year at Princeton University in the academic year 1957–1958. He worked for Bell Labs in Murray Hill, New Jersey from 1960 to 1995 and then for AT&T Labs in Florham Park, New Jersey from 1995 to 2000, when he retired. From 2000, Mallows was a consultant for Avaya Labs. He was t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Statistical Population
In statistics, a population is a set of similar items or events which is of interest for some question or experiment. A statistical population can be a group of existing objects (e.g. the set of all stars within the Milky Way galaxy) or a hypothetical and potentially infinite group of objects conceived as a generalization from experience (e.g. the set of all possible hands in a game of poker). A population with finitely many values N in the support of the population distribution is a finite population with population size N. A population with infinitely many values in the support is called infinite population. A common aim of statistical analysis is to produce information about some chosen population. In statistical inference, a subset of the population (a statistical '' sample'') is chosen to represent the population in a statistical analysis. Moreover, the statistical sample must be unbiased and accurately model the population. The ratio of the size of this statistical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |