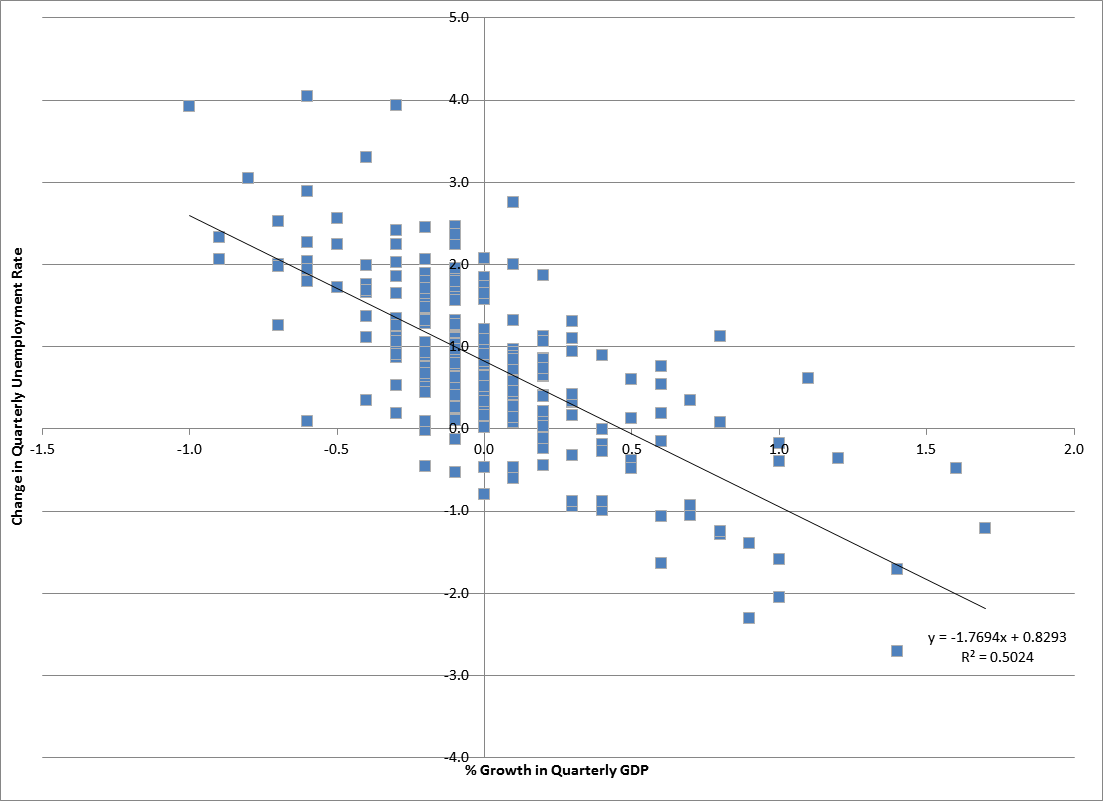
|
Path Analysis (statistics)
In statistics, path analysis is used to describe the directed dependencies among a set of variables. This includes models equivalent to any form of multiple regression analysis, factor analysis, canonical correlation analysis, discriminant analysis, as well as more general families of models in the multivariate analysis of variance and covariance analyses (MANOVA, ANOVA, ANCOVA). In addition to being thought of as a form of multiple regression focusing on causality, path analysis can be viewed as a special case of structural equation modeling (SEM) – one in which only single indicators are employed for each of the variables in the causal model. That is, path analysis is SEM with a structural model, but no measurement model. Other terms used to refer to path analysis include causal modeling and analysis of covariance structures. Path analysis is considered by Judea Pearl to be a direct ancestor to the techniques of Causal inference. History Path analysis was developed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Econometrics
Econometrics is the application of statistical methods to economic data in order to give empirical content to economic relationships.M. Hashem Pesaran (1987). "Econometrics," '' The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 p. 8–22 Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1p. 1–34Abstract (2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference". An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships". Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used today. A basic tool for econometrics is the multiple linear regression model. ''Econometric the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Structural Equation Models
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral sciences. A definition of SEM is difficult without reference to highly technical language, but a good starting place is the name itself. SEM involves the construction of a '' model'', to represent how various aspects of an observable or theoretical phenomenon are thought to be causally structurally related to one another. The '' structural'' aspect of the model implies theoretical associations between variables that represent the phenomenon under investigation. The postulated causal structuring is often depicted with arrows representing causal connections between variables (as in Figures 1 and 2) but these causal connections can be equivalently represented as equations. The causal structures imply that specific patterns of connections should ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Path Coefficient
Path coefficients are standardized versions of linear regression weights which can be used in examining the possible causal linkage between statistical variables in the structural equation modeling approach. The standardization involves multiplying the ordinary regression coefficient by the standard deviations of the corresponding explanatory variable: these can then be compared to assess the relative effects of the variables within the fitted regression model. The idea of standardization can be extended to apply to partial regression coefficients. The term "path coefficient" derives from Wright (1921), where a particular diagram-based approach was used to consider the relations between variables in a multivariate system.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. See also *Path analysis (statistics) In statistics, path analysis is used to describe the directed dependencies among a set of variables. This includes models equivalent to any form of multipl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Latent Variable Model
A latent variable model is a statistical model that relates a set of observable variables (also called ''manifest variables'' or ''indicators'') to a set of latent variables. It is assumed that the responses on the indicators or manifest variables are the result of an individual's position on the latent variable(s), and that the manifest variables have nothing in common after controlling for the latent variable (local independence). Different types of the latent variable models can be grouped according to whether the manifest and latent variables are categorical or continuous: The Rasch model represents the simplest form of item response theory. Mixture models are central to latent profile analysis. In factor analysis and latent trait analysis the latent variables are treated as continuous normally distributed variables, and in latent profile analysis and latent class analysis as from a multinomial distribution. The manifest variables in factor analysis and latent profil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Hidden Markov Model
A hidden Markov model (HMM) is a statistical Markov model in which the system being modeled is assumed to be a Markov process — call it X — with unobservable ("''hidden''") states. As part of the definition, HMM requires that there be an observable process Y whose outcomes are "influenced" by the outcomes of X in a known way. Since X cannot be observed directly, the goal is to learn about X by observing Y. HMM has an additional requirement that the outcome of Y at time t=t_0 must be "influenced" exclusively by the outcome of X at t=t_0 and that the outcomes of X and Y at t handwriting recognition, handwriting, gesture recognition, part-of-speech tagging, musical score following, partial discharges and bioinformatics. Definition Let X_n and Y_n be discrete-time stochastic processes and n\geq 1. The pair (X_n,Y_n) is a ''hidden Markov model'' if * X_n is a Markov process whose behavior is not directly observable ("hidden"); * \operatorname\bigl(Y_n \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Causal Loop Diagram
A causal loop diagram (CLD) is a causal diagram that aids in visualizing how different variables in a system are causally interrelated. The diagram consists of a set of words and arrows. Causal loop diagrams are accompanied by a narrative which describes the causally closed situation the CLD describes. Closed loops, or causal feedback loops, in the diagram are very important features of CLDs. The words with arrows coming in and out represent variables, or quantities whose value changes over time and the links represent a causal relationship between the two variables (i.e., they do not represent a material flow). A link marked + indicates a positive relation where an increase in the causal variable leads, all else equal, to an increase in the effect variable, or a decrease in the causal variable leads, all else equal, to a decrease in the effect variable. A link marked - indicates a negative relation where an increase in the causal variable leads, all else equal, to a decrease in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Bayesian Network
A Bayesian network (also known as a Bayes network, Bayes net, belief network, or decision network) is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases. Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (''e.g.'' speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams. Graphical m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Causality
Causality (also referred to as causation, or cause and effect) is influence by which one event, process, state, or object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cause is partly responsible for the effect, and the effect is partly dependent on the cause. In general, a process has many causes, which are also said to be ''causal factors'' for it, and all lie in its past. An effect can in turn be a cause of, or causal factor for, many other effects, which all lie in its future. Some writers have held that causality is metaphysically prior to notions of time and space. Causality is an abstraction that indicates how the world progresses. As such a basic concept, it is more apt as an explanation of other concepts of progression than as something to be explained by others more basic. The concept is like those of agency and efficacy. For this reason, a leap of intuition may be needed to grasp it. Acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Directed Acyclic Graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology (evolution, family trees, epidemiology) to information science (citation networks) to computation (scheduling). Directed acyclic graphs are sometimes instead called acyclic directed graphs or acyclic digraphs. Definitions A graph is formed by vertices and by edges connecting pairs of vertices, where the vertices can be any kind of object that is connected in pairs by edges. In the case of a directed graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Cycle (graph Theory)
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal. A graph without cycles is called an ''acyclic graph''. A directed graph without directed cycles is called a '' directed acyclic graph''. A connected graph without cycles is called a ''tree''. Definitions Circuit and cycle * A circuit is a non-empty trail in which the first and last vertices are equal (''closed trail''). : Let be a graph. A circuit is a non-empty trail with a vertex sequence . * A cycle or simple circuit is a circuit in which only the first and last vertices are equal. Directed circuit and directed cycle * A directed circuit is a non-empty directed trail in which the first and last vertices are equal (''closed directed trail''). : Let be a directed graph. A directed circuit is a non-empty directed trail with a vertex seq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |