|
Non-squeezing Theorem
The non-squeezing theorem, also called Gromov's non-squeezing theorem, is one of the most important theorems in symplectic geometry. It was first proven in 1985 by Mikhail Gromov. The theorem states that one cannot embed a ball into a cylinder via a symplectic map unless the radius of the ball is less than or equal to the radius of the cylinder. The theorem is important because formerly very little was known about the geometry behind symplectic maps. One easy consequence of a transformation being symplectic is that it preserves volume. One can easily embed a ball of any radius into a cylinder of any other radius by a volume-preserving transformation: just picture squeezing the ball into the cylinder (hence, the name non-squeezing theorem). Thus, the non-squeezing theorem tells us that, although symplectic transformations are volume-preserving, it is much more restrictive for a transformation to be symplectic than it is to be volume-preserving. Background and statement Consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symplectic Geometry
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the Hamiltonian formulation of classical mechanics where the phase space of certain classical systems takes on the structure of a symplectic manifold. The term "symplectic", introduced by Hermann Weyl, is a calque of "complex"; previously, the "symplectic group" had been called the "line complex group". "Complex" comes from the Latin ''com-plexus'', meaning "braided together" (co- + plexus), while symplectic comes from the corresponding Greek ''sym-plektikos'' (συμπλεκτικός); in both cases the stem comes from the Indo-European root *pleḱ- The name reflects the deep connections between complex and symplectic structures. By Darboux's theorem, symplectic manifolds are isomorphic to the standard symplectic vector space locally, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Maurice A
Maurice may refer to: * Maurice (name), a given name and surname, including a list of people with the name Places * or Mauritius Mauritius, officially the Republic of Mauritius, is an island country in the Indian Ocean, about off the southeastern coast of East Africa, east of Madagascar. It includes the main island (also called Mauritius), as well as Rodrigues, Ag ..., an island country in the Indian Ocean * Maurice, Iowa, a city * Maurice, Louisiana, a village * Maurice River, a tributary of the Delaware River in New Jersey Other uses * ''Maurice'' (2015 film), a Canadian short drama film * Maurice (horse), a Thoroughbred racehorse * ''Maurice'' (novel), a 1913 novel by E. M. Forster, published in 1971 ** ''Maurice'' (1987 film), a British film based on the novel * ''Maurice'' (Shelley), a children's story by Mary Shelley *Maurice, a character from the Madagascar ''franchise'' * Maurices, an American retail clothing chain *Maurice or Maryse, a type of cooking spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dusa McDuff
Dusa McDuff FRS CorrFRSE (born 18 October 1945) is an English mathematician who works on symplectic geometry. She was the first recipient of the Ruth Lyttle Satter Prize in Mathematics, was a Noether Lecturer, and is a Fellow of the Royal Society. She is currently the Helen Lyttle Kimmel '42 Professor of Mathematics at Barnard College. Personal life and education Margaret Dusa Waddington was born in London, England, on 18 October 1945 to Edinburgh architect Margaret Justin Blanco White, second wife of biologist Conrad Hal Waddington, her father. Her sister is the anthropologist Caroline Humphrey, and she has an elder half-brother C. Jake Waddington by her father's first marriage. Her mother was the daughter of Amber Reeves, the noted feminist, author and lover of H. G. Wells. McDuff grew up in Scotland where her father was Professor of Genetics at the University of Edinburgh. McDuff was educated at St George's School for Girls in Edinburgh and, although the standard was lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Canonical Coordinates
In mathematics and classical mechanics, canonical coordinates are sets of coordinates on phase space which can be used to describe a physical system at any given point in time. Canonical coordinates are used in the Hamiltonian formulation of classical mechanics. A closely related concept also appears in quantum mechanics; see the Stone–von Neumann theorem and canonical commutation relations for details. As Hamiltonian mechanics are generalized by symplectic geometry and canonical transformations are generalized by contact transformations, so the 19th century definition of canonical coordinates in classical mechanics may be generalized to a more abstract 20th century definition of coordinates on the cotangent bundle of a manifold (the mathematical notion of phase space). Definition in classical mechanics In classical mechanics, canonical coordinates are coordinates q^i and p_i in phase space that are used in the Hamiltonian formalism. The canonical coordinates satisfy the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Uncertainty Principle
The uncertainty principle, also known as Heisenberg's indeterminacy principle, is a fundamental concept in quantum mechanics. It states that there is a limit to the precision with which certain pairs of physical properties, such as position and momentum, can be simultaneously known. In other words, the more accurately one property is measured, the less accurately the other property can be known. More formally, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the product of the accuracy of certain related pairs of measurements on a quantum system, such as position, ''x'', and momentum, ''p''. Such paired-variables are known as complementary variables or canonically conjugate variables. First introduced in 1927 by German physicist Werner Heisenberg, the formal inequality relating the standard deviation of position ''σx'' and the standard deviation of momentum ''σp'' was derived by Earle Hesse Kennard later that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Liouville's Theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical mechanics, statistical and Hamiltonian mechanics. It asserts that ''the phase space, phase-space distribution function is constant along the Trajectory, trajectories of the system''—that is that the density of system points in the vicinity of a given system point traveling through phase-space is constant with time. This time-independent density is in statistical mechanics known as the classical a priori probability. Liouville's theorem applies to conservative systems, that is, systems in which the effects of friction are absent or can be ignored. The general mathematical formulation for such systems is the measure-preserving dynamical system. Liouville's theorem applies when there are degrees of freedom that can be interpreted as positions and momenta; not all measure-preserving dynamical systems have these, but Hamiltonian systems do. The general se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Canonical Transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates that preserves the form of Hamilton's equations. This is sometimes known as ''form invariance''. Although Hamilton's equations are preserved, it need not preserve the explicit form of the Hamiltonian itself. Canonical transformations are useful in their own right, and also form the basis for the Hamilton–Jacobi equations (a useful method for calculating conserved quantities) and Liouville's theorem (itself the basis for classical statistical mechanics). Since Lagrangian mechanics is based on generalized coordinates, transformations of the coordinates do not affect the form of Lagrange's equations and, hence, do not affect the form of Hamilton's equations if the momentum is simultaneously changed by a Legendre transformation into P_i = \frac\ , where \left\ are the new co‑ordinates, grouped in canonical conjugate pairs of momenta P_i and corresponding positions Q_i, for i = 1, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
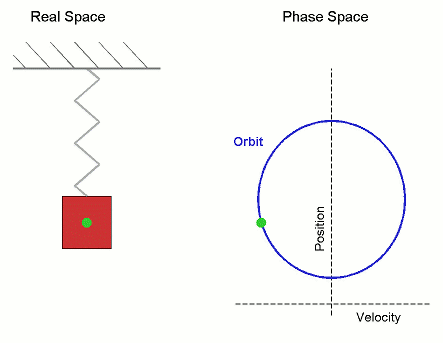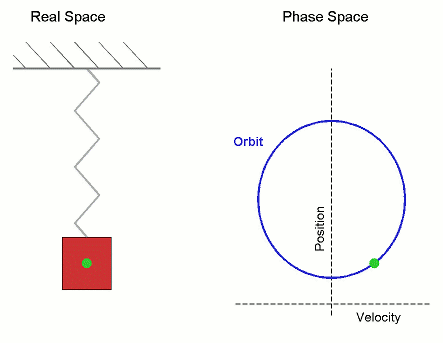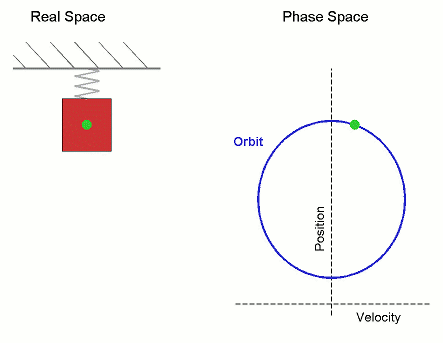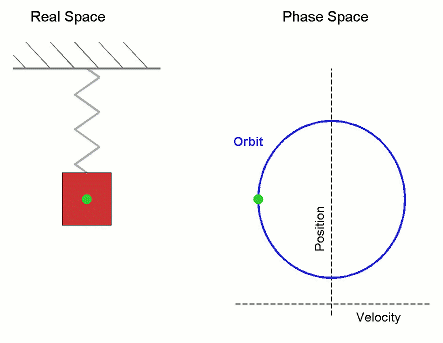
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Eye Of A Needle
The term "eye of a needle" is used as a metaphor for a very narrow opening. It occurs several times throughout the Talmud. The New Testament quotes Jesus as saying in Luke 18:25 that "it is easier for a camel to go through the eye of a needle than for a rich man to enter the kingdom of God" (Jesus and the rich young man); This is repeated in the same words in Matthew 19:24 and Mark 10:25. It also appears in the Qur'an 7:40, "Indeed, those who deny Our verses and are arrogant toward them – the gates of Heaven will not be opened for them, nor will they enter Paradise until a camel enters into the eye of a needle. And thus do We recompense the criminals." Aphorisms Judaism The Babylonian Talmud applies the aphorism to unthinkable thoughts. To explain that dreams reveal the thoughts of a man's heart and are the product of reason rather than the absence of it, some rabbis say: A midrash on the Song of Songs uses the phrase to speak of God's willingness and ability beyond compari ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mikhail Leonidovich Gromov
Mikhael Leonidovich Gromov (also Mikhail Gromov, Michael Gromov or Misha Gromov; ; born 23 December 1943) is a Russian-French mathematician known for his work in geometry, analysis and group theory. He is a permanent member of Institut des Hautes Études Scientifiques in France and a professor of mathematics at New York University. Gromov has won several prizes, including the Abel Prize in 2009 "for his revolutionary contributions to geometry". Early years, education and career Mikhail Gromov was born on 23 December 1943 in Boksitogorsk, Soviet Union. His father Leonid Gromov was Russian-Slavic and his mother Lea was of Jewish heritage. Both were pathologists. His mother was the cousin of World Chess Champion Mikhail Botvinnik, as well as of the mathematician Isaak Moiseevich Rabinovich. Gromov was born during World War II, and his mother, who worked as a medical doctor in the Soviet Army, had to leave the front line in order to give birth to him. When Gromov was nine years ol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ian Stewart (mathematician)
Ian Nicholas Stewart (born 24 September 1945) is a British mathematician and a popular-science and science-fiction writer. He is Emeritus Professor of Mathematics at the University of Warwick, England. Education and early life Stewart was born in 1945 in Folkestone, England. While in the sixth form at Harvey Grammar School in Folkestone he came to the attention of the mathematics teacher. The teacher had Stewart sit mock A-level examinations without any preparation along with the upper-sixth students; Stewart was placed first in the examination. He was awarded a scholarship to study at the University of Cambridge as an undergraduate student of Churchill College, Cambridge, where he studied the Mathematical Tripos and obtained a first-class Bachelor of Arts degree in mathematics in 1966. Stewart then went to the University of Warwick where his PhD on Lie algebras was supervised by Brian Hartley and completed in 1969. Career and research After his PhD, Stewart was offere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Embedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group (mathematics), group that is a subgroup. When some object X is said to be embedded in another object Y, the embedding is given by some Injective function, injective and structure-preserving map f:X\rightarrow Y. The precise meaning of "structure-preserving" depends on the kind of mathematical structure of which X and Y are instances. In the terminology of category theory, a structure-preserving map is called a morphism. The fact that a map f:X\rightarrow Y is an embedding is often indicated by the use of a "hooked arrow" (); thus: f : X \hookrightarrow Y. (On the other hand, this notation is sometimes reserved for inclusion maps.) Given X and Y, several different embeddings of X in Y may be possible. In many cases of interest there is a standard (or "canonical") embedding, like those of the natural numbers in the integers, the integers i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |