|
Negentropy
In information theory and statistics, negentropy is used as a measure of distance to normality. It is also known as negative entropy or syntropy. Etymology The concept and phrase "''negative entropy''" was introduced by Erwin Schrödinger in his 1944 book '' What is Life?.'' Later, French physicist Léon Brillouin shortened the phrase to (). In 1974, Albert Szent-Györgyi proposed replacing the term ''negentropy'' with ''syntropy''. That term may have originated in the 1940s with the Italian mathematician Luigi Fantappiè, who tried to construct a unified theory of biology and physics. Buckminster Fuller tried to popularize this usage, but ''negentropy'' remains common. In a note to ''What is Life?,'' Schrödinger explained his use of this phrase: Information theory In information theory and statistics, negentropy is used as a measure of distance to normality. Out of all probability distributions with a given mean and variance, the Gaussian or normal distribution is th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy And Life
Research concerning the relationship between the thermodynamic quantity entropy and both the origin and evolution of life began around the turn of the 20th century. In 1910 American historian Henry Adams printed and distributed to university libraries and history professors the small volume ''A Letter to American Teachers of History'' proposing a theory of history based on the second law of thermodynamics and on the principle of entropy. The 1944 book '' What is Life?'' by Nobel-laureate physicist Erwin Schrödinger stimulated further research in the field. In his book, Schrödinger originally stated that life feeds on negative entropy, or negentropy as it is sometimes called, but in a later edition corrected himself in response to complaints and stated that the true source is free energy. More recent work has restricted the discussion to Gibbs free energy because biological processes on Earth normally occur at a constant temperature and pressure, such as in the atmosphere or at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Léon Brillouin
Léon Nicolas Brillouin (; August 7, 1889 – October 4, 1969) was a French physicist. He made contributions to quantum mechanics, radio wave propagation in the atmosphere, solid-state physics, and information theory. Early life Brillouin was born in Sèvres, near Paris, France. His father, Marcel Brillouin, grandfather, Éleuthère Mascart, and great-grandfather, Charles Briot, were physicists as well. Education From 1908 to 1912, Brillouin studied physics at the École Normale Supérieure, in Paris. From 1911 he studied under Jean Perrin until he left for the Ludwig Maximilian University of Munich (LMU), in 1912. At LMU, he studied theoretical physics with Arnold Sommerfeld. Just a few months before Brillouin's arrival at LMU, Max von Laue had conducted his experiment showing X-ray diffraction in a crystal lattice. In 1913, he went back to France to study at the University of Paris and it was in this year that Niels Bohr submitted his first paper on the Bohr model of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Luigi Fantappiè
Luigi Fantappiè (15 September 1901 – 28 July 1956) was an Italian mathematician, known for work in mathematical analysis and for creating the theory of analytic functionals: he was a student and follower of Vito Volterra. Later in life, he proposed scientific theories of sweeping scope. Biography Luigi Fantappiè was born in Viterbo, and studied at the University of Pisa, graduating in mathematics in 1922. After time spent abroad, he was offered a chair by the University of Florence in 1926, and a year later by the University of Palermo. He spent the years 1934 to 1939 in the University of São Paulo, Brazil collaborating with Benedito Castrucci notorious Italian-Brazilian mathematician. In 1939 he was offered a chair at the University of Rome. In 1941 he discovered that negative entropy has qualities that are associated with life: The cause of processes driven by negative energy lies in the future, exactly such as living beings work for a better day tomorrow. A proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change and information systems including the transmission of information in telecommunication. Entropy is central to the second law of thermodynamics, which states that the entropy of an isolated system left to spontaneous evolution cannot decrease with time. As a result, isolated systems evolve toward thermodynamic equilibrium, where the entropy is highest. A consequence of the second law of thermodynamics is that certain processes are irreversible. The thermodynami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis. In 1863, Yale University awarded Gibbs the firs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Free Enthalpy
In thermodynamics, the Gibbs free energy (or Gibbs energy as the recommended name; symbol is a thermodynamic potential that can be used to calculate the maximum amount of work, other than pressure–volume work, that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy is expressed as G(p,T) = U + pV - TS = H - TS where: * U is the internal energy of the system * H is the enthalpy of the system * S is the entropy of the system * T is the temperature of the system * V is the volume of the system * p is the pressure of the system (which must be equal to that of the surroundings for mechanical equilibrium). The Gibbs free energy change (, measured in joules in SI) is the ''maximum'' amount of non-volume expansion work that can be extracted from a closed system (one that can exchange heat and work with i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
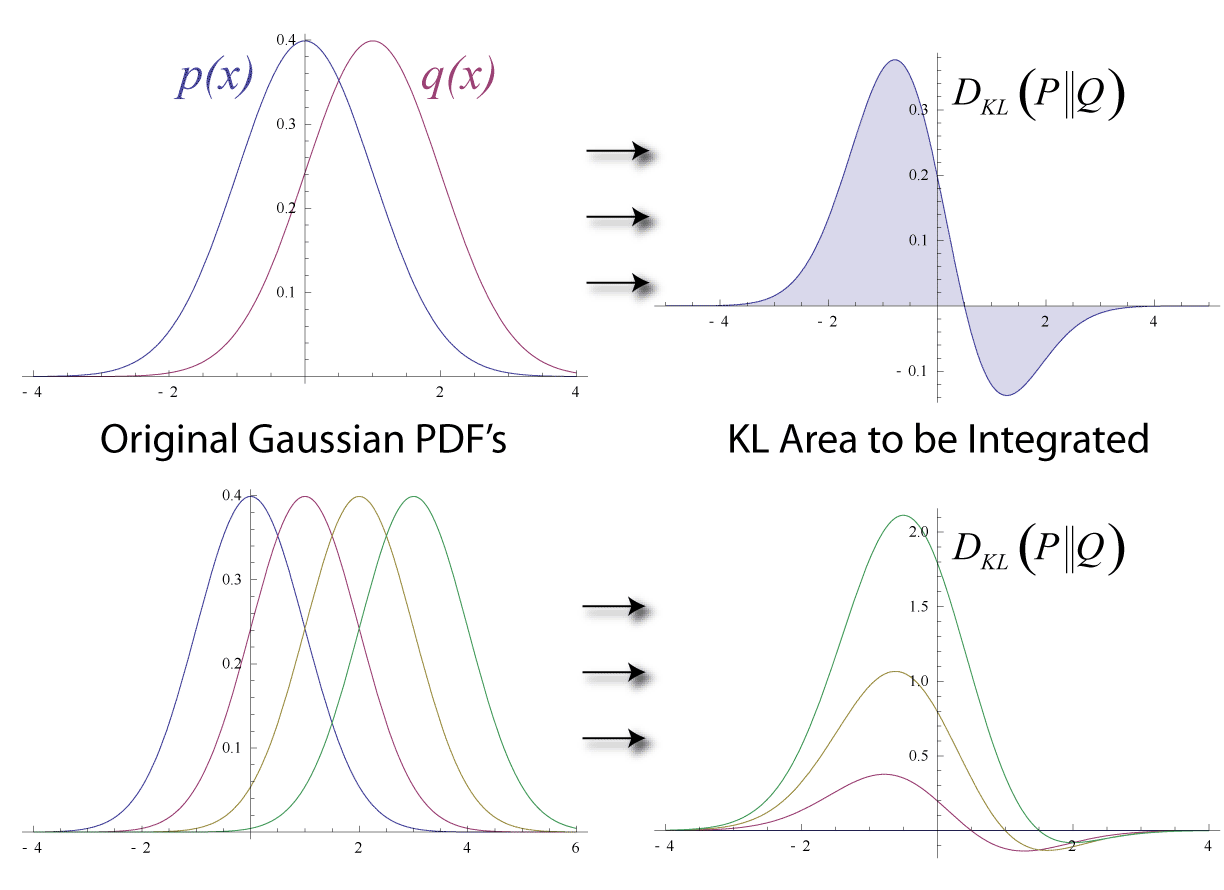
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Component Analysis
In signal processing, independent component analysis (ICA) is a computational method for separating a multivariate statistics, multivariate signal into additive subcomponents. This is done by assuming that at most one subcomponent is Gaussian and that the subcomponents are Statistical independence, statistically independent from each other. ICA was invented by Jeanny Hérault and Christian Jutten in 1985. ICA is a special case of blind source separation. A common example application of ICA is the "cocktail party problem" of listening in on one person's speech in a noisy room. Introduction Independent component analysis attempts to decompose a multivariate signal into independent non-Gaussian signals. As an example, sound is usually a signal that is composed of the numerical addition, at each time t, of signals from several sources. The question then is whether it is possible to separate these contributing sources from the observed total signal. When the statistical independence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Entropy
In network science, the network entropy is a disorder measure derived from information theory to describe the level of randomness and the amount of information encoded in a graph. It is a relevant metric to quantitatively characterize real complex networks and can also be used to quantify network complexity Formulations According to a 2018 publication by Zenil ''et al.'' there are several formulations by which to calculate network entropy and, as a rule, they all require a particular property of the graph to be focused, such as the adjacency matrix, degree sequence, degree distribution or number of bifurcations, what might lead to values of entropy that aren't invariant to the chosen network description. Degree Distribution Shannon Entropy The Shannon entropy can be measured for the network degree probability distribution as an average measurement of the heterogeneity of the network. \mathcal = - \sum_^ P(k) \ln This formulation has limited use with regards to complexity, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |