|
Microcontinuity
In nonstandard analysis, a discipline within classical mathematics, microcontinuity (or ''S''-continuity) of an internal function ''f'' at a point ''a'' is defined as follows: :for all ''x'' infinitely close to ''a'', the value ''f''(''x'') is infinitely close to ''f''(''a''). Here ''x'' runs through the domain of ''f''. In formulas, this can be expressed as follows: :if x\approx a then f(x)\approx f(a). For a function ''f'' defined on \mathbb, the definition can be expressed in terms of the halo as follows: ''f'' is microcontinuous at c\in\mathbb if and only if f(hal(c))\subseteq hal(f(c)), where the natural extension of ''f'' to the hyperreals is still denoted ''f''. Alternatively, the property of microcontinuity at ''c'' can be expressed by stating that the composition \text\circ f is constant on the halo of ''c'', where "st" is the standard part function. History The modern property of continuity of a function was first defined by Bolzano in 1817. However, Bolzano's work ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonstandard Analysis
The history of calculus is fraught with philosophical debates about the meaning and logical validity of fluxions or infinitesimal numbers. The standard way to resolve these debates is to define the operations of calculus using (ε, δ)-definition of limit, epsilon–delta procedures rather than infinitesimals. Nonstandard analysis instead reformulates the calculus using a logically rigorous notion of infinitesimal numbers. Nonstandard analysis originated in the early 1960s by the mathematician Abraham Robinson. He wrote: ... the idea of infinitely small or ''infinitesimal'' quantities seems to appeal naturally to our intuition. At any rate, the use of infinitesimals was widespread during the formative stages of the Differential and Integral Calculus. As for the objection ... that the distance between two distinct real numbers cannot be infinitely small, Gottfried Wilhelm Leibniz argued that the theory of infinitesimals implies the introduction of ideal numbers which might be inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Part Function
In nonstandard analysis, the standard part function is a function from the limited (finite) hyperreal numbers to the real numbers. Briefly, the standard part function "rounds off" a finite hyperreal to the nearest real. It associates to every such hyperreal x, the unique real x_0 infinitely close to it, i.e. x-x_0 is infinitesimal. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de Fermat,Karin Usadi Katz and Mikhail G. Katz (2011) A Burgessian Critique of Nominalistic Tendencies in Contemporary Mathematics and its Historiography. Foundations of Science.Searxiv The authors refer to the Fermat-Robinson standard part. as well as Leibniz's Transcendental law of homogeneity. The standard part function was first defined by Abraham Robinson who used the notation ^x for the standard part of a hyperreal x (see Robinson 1974). This concept plays a key role in defining the concepts of the calculus, such as continuity, the deri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
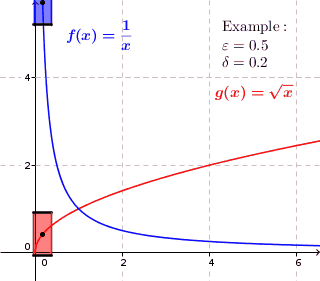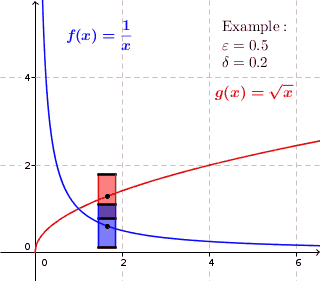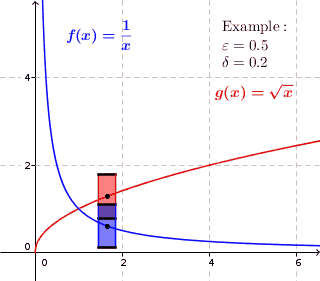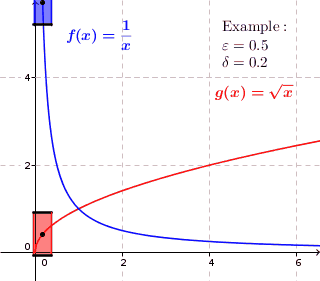
Uniformly Continuous
In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number \epsilon, then there is a positive real number \delta such that , f(x) - f(y), 0 there exists a real number \delta > 0 such that for every x,y \in X with d_1(x,y) 0 such that for every x,y \in X , , x - y, 0 \; \forall x \in X \; \forall y \in X : \, d_1(x,y) 0 , \forall x \in X , and \forall y \in X ) are used. * Alternatively, f is said to be uniformly continuous if there is a function of all positive real numbers \varepsilon, \delta(\varepsilon) representing the maximum positive real number, such that for every x,y \in X if d_1(x,y) 0 such that for every y \in X wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Convergence
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions (f_n) converges uniformly to a limiting function f on a set E if, given any arbitrarily small positive number \epsilon, a number N can be found such that each of the functions f_N, f_,f_,\ldots differs from f by no more than \epsilon ''at every point'' x ''in'' E. Described in an informal way, if f_n converges to f uniformly, then the rate at which f_n(x) approaches f(x) is "uniform" throughout its domain in the following sense: in order to guarantee that f_n(x) falls within a certain distance \epsilon of f(x), we do not need to know the value of x\in E in question — there can be found a single value of N=N(\epsilon) ''independent of x'', such that choosing n\geq N will ensure that f_n(x) is within \epsilon of f(x) ''for all x\in E''. In contrast, pointwise convergence of f_n to f merely guarantees that for any x\in E giv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Part Function
In nonstandard analysis, the standard part function is a function from the limited (finite) hyperreal numbers to the real numbers. Briefly, the standard part function "rounds off" a finite hyperreal to the nearest real. It associates to every such hyperreal x, the unique real x_0 infinitely close to it, i.e. x-x_0 is infinitesimal. As such, it is a mathematical implementation of the historical concept of adequality introduced by Pierre de Fermat,Karin Usadi Katz and Mikhail G. Katz (2011) A Burgessian Critique of Nominalistic Tendencies in Contemporary Mathematics and its Historiography. Foundations of Science.Searxiv The authors refer to the Fermat-Robinson standard part. as well as Leibniz's Transcendental law of homogeneity. The standard part function was first defined by Abraham Robinson who used the notation ^x for the standard part of a hyperreal x (see Robinson 1974). This concept plays a key role in defining the concepts of the calculus, such as continuity, the deri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Mathematics
In the foundations of mathematics, classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. It stands in contrast to other types of mathematics such as constructive mathematics or predicative mathematics. In practice, the most common non-classical systems are used in constructive mathematics. Classical mathematics is sometimes attacked on philosophical grounds, due to constructivist and other objections to the logic, set theory, etc., chosen as its foundations, such as have been expressed by L. E. J. Brouwer. Almost all mathematics, however, is done in the classical tradition, or in ways compatible with it. Defenders of classical mathematics, such as David Hilbert, have argued that it is easier to work in, and is most fruitful; although they acknowledge non-classical mathematics has at times led to fruitful results that classical mathematics could not (or could not so easily) attain, they argue t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Internal Function
In mathematical logic, in particular in model theory and nonstandard analysis, an internal set is a set that is a member of a model. The concept of internal sets is a tool in formulating the transfer principle, which concerns the logical relation between the properties of the real numbers R, and the properties of a larger field denoted *R called the hyperreal numbers. The field *R includes, in particular, infinitesimal ("infinitely small") numbers, providing a rigorous mathematical justification for their use. Roughly speaking, the idea is to express analysis over R in a suitable language of mathematical logic, and then point out that this language applies equally well to *R. This turns out to be possible because at the set-theoretic level, the propositions in such a language are interpreted to apply only to internal sets rather than to all sets (note that the term "language" is used in a loose sense in the above). Edward Nelson's internal set theory is an axiomatic approach ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halo (mathematics)
In nonstandard analysis, a monad (also called halo) is the set of points infinitesimally close to a given point. Given a hyperreal number ''x'' in R∗, the monad of ''x'' is the set :\text(x)=\. If ''x'' is finite (limited), the unique real number in the monad of ''x'' is called the standard part of ''x''. See also *Infinitesimal In mathematics, an infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally re ... Notes References H. Jerome Keisler: Foundations of Infinitesimal Calculus, available for downloading Nonstandard analysis {{mathanalysis-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperreal Number
In mathematics, the system of hyperreal numbers is a way of treating infinite and infinitesimal (infinitely small but non-zero) quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form :1 + 1 + \cdots + 1 (for any finite number of terms). Such numbers are infinite, and their reciprocals are infinitesimals. The term "hyper-real" was introduced by Edwin Hewitt in 1948. The hyperreal numbers satisfy the transfer principle, a rigorous version of Leibniz's heuristic law of continuity. The transfer principle states that true first-order statements about R are also valid in *R. For example, the commutative law of addition, , holds for the hyperreals just as it does for the reals; since R is a real closed field, so is *R. Since \sin()=0 for all integers ''n'', one also has \sin()=0 for all hyperintegers H. The transfer principle for ultrapowers is a consequence of Łoś' theorem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy
Baron Augustin-Louis Cauchy (, ; ; 21 August 178923 May 1857) was a French mathematician, engineer, and physicist who made pioneering contributions to several branches of mathematics, including mathematical analysis and continuum mechanics. He was one of the first to state and rigorously prove theorems of calculus, rejecting the heuristic principle of the generality of algebra of earlier authors. He almost singlehandedly founded complex analysis and the study of permutation groups in abstract algebra. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific writer; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. Bio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cours D'Analyse
''Cours d'Analyse de l’École Royale Polytechnique; I.re Partie. Analyse algébrique'' is a seminal textbook in infinitesimal calculus published by Augustin-Louis Cauchy in 1821. The article follows the translation by Bradley and Sandifer in describing its contents. Introduction On page 1 of the Introduction, Cauchy writes: "In speaking of the continuity of functions, I could not dispense with a treatment of the principal properties of infinitely small quantities, properties which serve as the foundation of the infinitesimal calculus." The translators comment in a footnote: "It is interesting that Cauchy does not also mention limits here." Cauchy continues: "As for the methods, I have sought to give them all the rigor which one demands from geometry, so that one need never rely on arguments drawn from the generality of algebra." Preliminaries On page 6, Cauchy first discusses variable quantities and then introduces the limit notion in the following terms: "When the value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal
In mathematics, an infinitesimal number is a quantity that is closer to zero than any standard real number, but that is not zero. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " infinity- th" item in a sequence. Infinitesimals do not exist in the standard real number system, but they do exist in other number systems, such as the surreal number system and the hyperreal number system, which can be thought of as the real numbers augmented with both infinitesimal and infinite quantities; the augmentations are the reciprocals of one another. Infinitesimal numbers were introduced in the development of calculus, in which the derivative was first conceived as a ratio of two infinitesimal quantities. This definition was not rigorously formalized. As calculus developed further, infinitesimals were replaced by limits, which can be calculated using the standard real numbers. Infinitesimals regained pop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |