|
Multiply-with-carry
In computer science, multiply-with-carry (MWC) is a method invented by George Marsaglia for generating sequences of random integers based on an initial set from two to many thousands of randomly chosen seed values. The main advantages of the MWC method are that it invokes simple computer integer arithmetic and leads to very fast generation of sequences of random numbers with immense periods, ranging from around 2^ to 2^. As with all pseudorandom number generators, the resulting sequences are functions of the supplied seed values. General theory An MWC generator is a special form of Lehmer random number generator x_n = bx_ \bmod p which allows efficient implementation of a prime modulus p much larger than the machine word size. Normal Lehmer generator implementations choose a modulus close to the machine word size. An MWC generator instead maintains its state in base b, so multiplying by b is done implicitly by shifting one word. The base b is typically chosen to equal the compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Random Number Generators
Random number generators are important in many kinds of technical applications, including physics, engineering or mathematical computer studies (e.g., Monte Carlo simulations), cryptography and gambling (on game servers). This list includes many common types, regardless of quality or applicability to a given use case. Pseudorandom number generators (PRNGs) The following algorithms are pseudorandom number generators. Cryptographic algorithms Cipher algorithms and cryptographic hashes can be used as very high-quality pseudorandom number generators. However, generally they are considerably slower (typically by a factor 2–10) than fast, non-cryptographic random number generators. These include: * Stream ciphers. Popular choices are Salsa20 or ChaCha (often with the number of rounds reduced to 8 for speed), ISAAC, HC-128 and RC4. * Block ciphers in counter mode. Common choices are AES (which is very fast on systems supporting it in hardware), TwoFish, Serpent and Camel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
George Marsaglia
George Marsaglia (March 12, 1924 – February 15, 2011) was an American mathematician and computer scientist. He is best known for creating the diehard tests, a suite of software for measuring statistical randomness. Research on random numbers George Marsaglia established the lattice structure of linear congruential generators in the paper "Random numbers fall mainly in the planes", later termed Marsaglia's theorem. This phenomenon means that ''n''-tuples with coordinates obtained from consecutive use of the generator will lie on a small number of equally spaced hyperplanes in ''n''-dimensional space. He also developed the diehard tests, a series of tests to determine whether or not a sequence of numbers have the statistical properties that could be expected from a random sequence. In 1995 he published a CD-ROM of random numbers, which included the diehard tests. His diehard paper came with the quotation "Nothing is random, only uncertain" attributed to ''Gail Gasram'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mersenne Twister
The Mersenne Twister is a general-purpose pseudorandom number generator (PRNG) developed in 1997 by and . Its name derives from the choice of a Mersenne prime as its period length. The Mersenne Twister was created specifically to address most of the flaws found in earlier PRNGs. The most commonly used version of the Mersenne Twister algorithm is based on the Mersenne prime 2^-1. The standard implementation of that, MT19937, uses a 32-bit word length. There is another implementation (with five variants) that uses a 64-bit word length, MT19937-64; it generates a different sequence. ''k''-distribution A pseudorandom sequence x_i of ''w''-bit integers of period ''P'' is said to be ''k-distributed'' to ''v''-bit accuracy if the following holds. : Let trunc''v''(''x'') denote the number formed by the leading ''v'' bits of ''x'', and consider ''P'' of the ''kv''-bit vectors :: (\operatorname_v(x_i), \operatorname_v(x_), \, \ldots, \operatorname_v(x_)) \quad (0\leq i. The Mersenn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Roguelike
Roguelike (or rogue-like) is a style of role-playing game traditionally characterized by a dungeon crawl through procedurally generated levels, turn-based gameplay, grid-based movement, and permanent death of the player character. Most roguelikes are based on a high fantasy narrative, reflecting the influence of tabletop role-playing games such as ''Dungeons & Dragons''. Though '' Beneath Apple Manor'' predates it, the 1980 game '' Rogue'', which is an ASCII based game that runs in terminal or terminal emulator, is considered the forerunner and the namesake of the genre, with derivative games mirroring ''Rogue''s Text-based game, character- or Sprite (computer graphics), sprite-based graphics. These games were popularized among college students and computer programmers of the 1980s and 1990s, leading to hundreds of variants. Some of the better-known variants include ''Hack (video game), Hack'', ''NetHack'', ''Ancient Domains of Mystery'', ''Moria (1983 video game), Moria' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
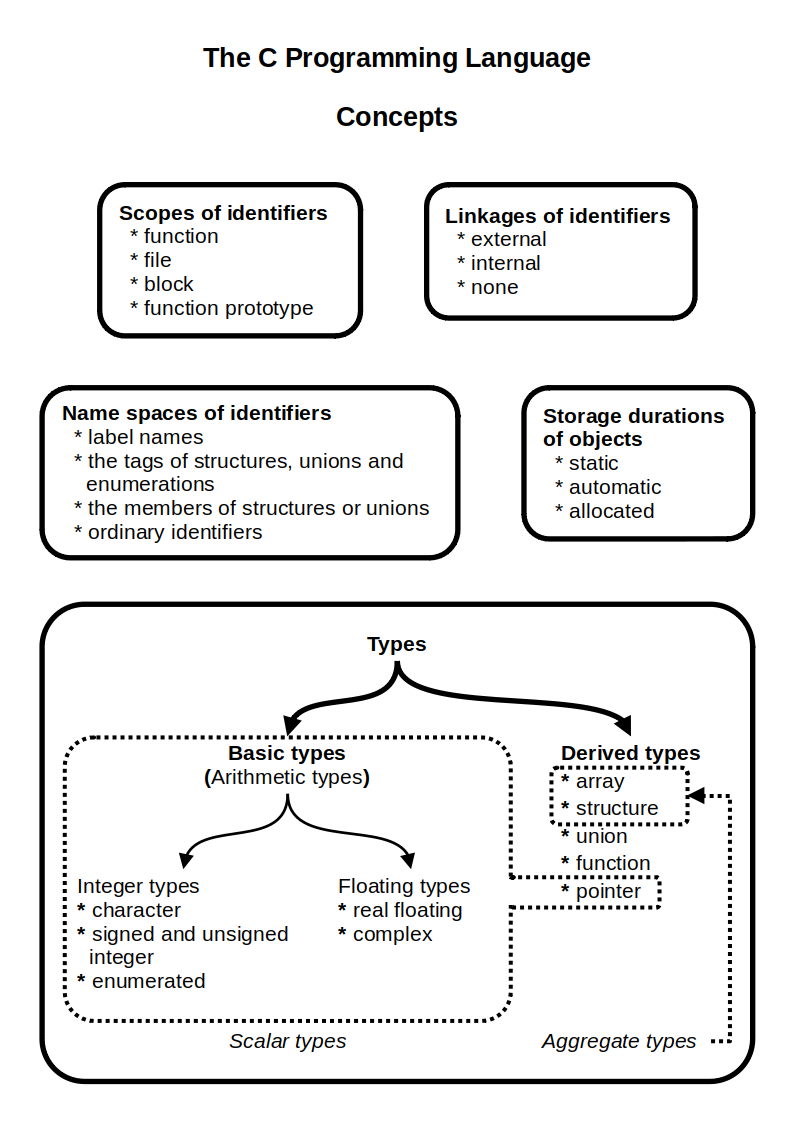
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Relatively Prime
In number theory, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also ''is prime to'' or ''is coprime with'' . The numbers 8 and 9 are coprime, despite the fact that neither—considered individually—is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing When the integers and are coprime, the standard way of expressing this fact in mathematical notation is to indicate that their greatest common divisor is one, by the formula or . In their 1989 textbook '' Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed an alter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Equidistributed
In mathematics, a sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be equidistributed, or uniformly distributed, if the proportion of terms falling in a subinterval is proportional to the length of that subinterval. Such sequences are studied in Diophantine approximation theory and have applications to Monte Carlo integration. Definition A sequence (''s''1, ''s''2, ''s''3, ...) of real numbers is said to be ''equidistributed'' on a non-degenerate interval 'a'', ''b''if for every subinterval 'c'', ''d''of 'a'', ''b''we have :\lim_= . (Here, the notation , ∩ 'c'', ''d'' denotes the number of elements, out of the first ''n'' elements of the sequence, that are between ''c'' and ''d''.) For example, if a sequence is equidistributed in , 2 since the interval .5, 0.9occupies 1/5 of the length of the interval , 2 as ''n'' becomes large, the proportion of the first ''n'' members of the sequence which fall between 0.5 and 0.9 must approach 1/5. L ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Repeating Decimal
A repeating decimal or recurring decimal is a decimal representation of a number whose digits are eventually periodic (that is, after some place, the same sequence of digits is repeated forever); if this sequence consists only of zeros (that is if there is only a finite number of nonzero digits), the decimal is said to be ''terminating'', and is not considered as repeating. It can be shown that a number is rational if and only if its decimal representation is repeating or terminating. For example, the decimal representation of becomes periodic just after the decimal point, repeating the single digit "3" forever, i.e. 0.333.... A more complicated example is , whose decimal becomes periodic at the ''second'' digit following the decimal point and then repeats the sequence "144" forever, i.e. 5.8144144144.... Another example of this is , which becomes periodic after the decimal point, repeating the 13-digit pattern "1886792452830" forever, i.e. 11.18867924528301886792452830.... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Radix
In a positional numeral system, the radix (radices) or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal system (the most common system in use today) the radix is ten, because it uses the ten digits from 0 through 9. In any standard positional numeral system, a number is conventionally written as with ''x'' as the string of digits and ''y'' as its base. For base ten, the subscript is usually assumed and omitted (together with the enclosing parentheses), as it is the most common way to express value. For example, (the decimal system is implied in the latter) and represents the number one hundred, while (100)2 (in the binary system with base 2) represents the number four. Etymology ''Radix'' is a Latin word for "root". ''Root'' can be considered a synonym for ''base,'' in the arithmetical sense. In numeral systems Generally, in a system with radix ''b'' (), a string of digits denotes the number , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Safe Prime
In number theory, a prime number ''p'' is a if 2''p'' + 1 is also prime. The number 2''p'' + 1 associated with a Sophie Germain prime is called a . For example, 11 is a Sophie Germain prime and 2 × 11 + 1 = 23 is its associated safe prime. Sophie Germain primes and safe primes have applications in public key cryptography and primality testing. It has been conjectured that there are infinitely many Sophie Germain primes, but this remains unproven. Sophie Germain primes are named after French mathematician Sophie Germain, who used them in her investigations of Fermat's Last Theorem. One attempt by Germain to prove Fermat’s Last Theorem was to let ''p'' be a prime number of the form 8''k'' + 7 and to let ''n'' = ''p'' – 1. In this case, x^n + y^n = z^n is unsolvable. Germain’s proof, however, remained unfinished. Through her attempts to solve Fermat's Last Theorem, Germain developed a result now known as Germain's Theore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fermat's Little Theorem
In number theory, Fermat's little theorem states that if is a prime number, then for any integer , the number is an integer multiple of . In the notation of modular arithmetic, this is expressed as a^p \equiv a \pmod p. For example, if and , then , and is an integer multiple of . If is not divisible by , that is, if is coprime to , then Fermat's little theorem is equivalent to the statement that is an integer multiple of , or in symbols: a^ \equiv 1 \pmod p. For example, if and , then , and is a multiple of . Fermat's little theorem is the basis for the Fermat primality test and is one of the fundamental results of elementary number theory. The theorem is named after Pierre de Fermat, who stated it in 1640. It is called the "little theorem" to distinguish it from Fermat's Last Theorem.. History Pierre de Fermat first stated the theorem in a letter dated October 18, 1640, to his friend and confidant Frénicle de Bessy. His formulation is equivalent to the following ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |