|
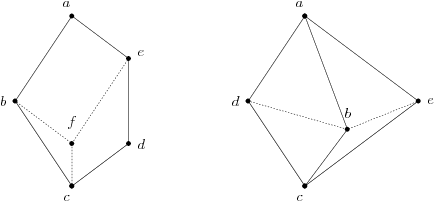
Modular Lattice
In the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self- dual condition, ;Modular law: implies where are arbitrary elements in the lattice, ≤ is the partial order, and ∨ and ∧ (called join and meet respectively) are the operations of the lattice. This phrasing emphasizes an interpretation in terms of projection onto the sublattice , a fact known as the diamond isomorphism theorem. An alternative but equivalent condition stated as an equation (see below) emphasizes that modular lattices form a variety in the sense of universal algebra. Modular lattices arise naturally in algebra and in many other areas of mathematics. In these scenarios, modularity is an abstraction of the 2nd Isomorphism Theorem. For example, the subspaces of a vector space (and more generally the submodules of a module over a ring) form a modular lattice. In a not necessarily modular lattice, there may ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2d Modular Lattice
D, or d, is the fourth Letter (alphabet), letter of the Latin alphabet, used in the English alphabet, modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is English alphabet#Letter names, ''dee'' (pronounced ), plural ''dees''. History The Semitic languages, Semitic letter Daleth, Dāleth may have developed from the logogram for a fish or a door. There are many different Egyptian hieroglyphs that might have inspired this. In Semitic, Ancient Greek and Latin, the letter represented ; in the Etruscan alphabet the letter was archaic but still retained. The equivalent Greek letter is delta, Delta (letter), Δ. The lower case, minuscule (lower-case) form of 'd' consists of a lower-story left Typeface anatomy#Strokes, bowl and a Typeface anatomy#Strokes, stem ascender. It most likely developed by gradual variations on the upper case, majuscule (capital) form 'D', and is now composed as a stem with a full Typeface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sublattice
A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every pair of elements has a unique supremum (also called a least upper bound or join) and a unique infimum (also called a greatest lower bound or meet). An example is given by the power set of a set, partially ordered by inclusion, for which the supremum is the union and the infimum is the intersection. Another example is given by the natural numbers, partially ordered by divisibility, for which the supremum is the least common multiple and the infimum is the greatest common divisor. Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities. Since the two definitions are equivalent, lattice theory draws on both order theory and universal algebra. Semilattices include lattices, which in turn include Heyting and Boolean algebras. These ''lattice-like'' structures all admi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ascending Chain Condition
In mathematics, the ascending chain condition (ACC) and descending chain condition (DCC) are finiteness properties satisfied by some algebraic structures, most importantly Ideal (ring theory), ideals in certain commutative rings. These conditions played an important role in the development of the structure theory of commutative rings in the works of David Hilbert, Emmy Noether, and Emil Artin. The conditions themselves can be stated in an abstract form, so that they make sense for any partially ordered set. This point of view is useful in abstract algebraic dimension theory due to Gabriel and Rentschler. Definition A partially ordered set (poset) ''P'' is said to satisfy the ascending chain condition (ACC) if no infinite strictly ascending sequence : a_1 < a_2 < a_3 < \cdots of elements of ''P'' exists. Equivalently, every weakly ascending sequence : of elements of ''P'' eventually stabilizes, meaning that there exists a pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
French Language
French ( or ) is a Romance languages, Romance language of the Indo-European languages, Indo-European family. Like all other Romance languages, it descended from the Vulgar Latin of the Roman Empire. French evolved from Northern Old Gallo-Romance, a descendant of the Latin spoken in Northern Gaul. Its closest relatives are the other langues d'oïl—languages historically spoken in northern France and in southern Belgium, which French (Francien language, Francien) largely supplanted. It was also substratum (linguistics), influenced by native Celtic languages of Northern Roman Gaul and by the Germanic languages, Germanic Frankish language of the post-Roman Franks, Frankish invaders. As a result of French and Belgian colonialism from the 16th century onward, it was introduced to new territories in the Americas, Africa, and Asia, and numerous French-based creole languages, most notably Haitian Creole, were established. A French-speaking person or nation may be referred to as Fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Theorem
In group theory, the correspondence theorem (also the lattice theorem,W.R. Scott: ''Group Theory'', Prentice Hall, 1964, p. 27. and variously and ambiguously the third and fourth isomorphism theorem ) states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G containing N, onto the set of all subgroups of the quotient group G/N. Loosely speaking, the structure of the subgroups of G/N is exactly the same as the structure of the subgroups of G containing N, with N collapsed to the identity element. Specifically, if : G is a group, : N \triangleleft G, a normal subgroup of G, : \mathcal = \, the set of all subgroups A of G that contain N, and : \mathcal = \, the set of all subgroups of G/N, then there is a bijective map \phi: \mathcal \to \mathcal such that : \phi(A) = A/N for all A \in \mathcal. One further has that if A and B are in \mathcal then * A \subseteq B if and only if A/N \subseteq B/N; * if A \subsete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isomorphism Theorem
In mathematics, specifically abstract algebra, the isomorphism theorems (also known as Noether's isomorphism theorems) are theorems that describe the relationship among quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and other algebraic structures. In universal algebra, the isomorphism theorems can be generalized to the context of algebras and congruences. History The isomorphism theorems were formulated in some generality for homomorphisms of modules by Emmy Noether in her paper ''Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern'', which was published in 1927 in Mathematische Annalen. Less general versions of these theorems can be found in work of Richard Dedekind and previous papers by Noether. Three years later, B.L. van der Waerden published his influential '' Moderne Algebra'', the first abstract algebra textbook that took the groups- rings- fields ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annals Of Mathematics
The ''Annals of Mathematics'' is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study. History The journal was established as ''The Analyst'' in 1874 and with Joel E. Hendricks as the founding editor-in-chief. It was "intended to afford a medium for the presentation and analysis of any and all questions of interest or importance in pure and applied Mathematics, embracing especially all new and interesting discoveries in theoretical and practical astronomy, mechanical philosophy, and engineering". It was published in Des Moines, Iowa, and was the earliest American mathematics journal to be published continuously for more than a year or two. This incarnation of the journal ceased publication after its tenth year, in 1883, giving as an explanation Hendricks' declining health, but Hendricks made arrangements to have it taken over by new management, and it was continued from March 1884 as the ''Annals of Mathematics''. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributive Lattice
In mathematics, a distributive lattice is a lattice (order), lattice in which the operations of join and meet distributivity, distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union (set theory), union and intersection (set theory), intersection. Indeed, these lattices of sets describe the scenery completely: every distributive lattice is—up to order isomorphism, isomorphism—given as such a lattice of sets. Definition As in the case of arbitrary lattices, one can choose to consider a distributive lattice ''L'' either as a structure of order theory or of universal algebra. Both views and their mutual correspondence are discussed in the article on lattice (order), lattices. In the present situation, the algebraic description appears to be more convenient. A lattice (''L'',∨,∧) is distributive if the following additional identity holds for all ''x'', ''y'', and ''z'' i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the n-gon, -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition The word "dihedral" comes from "di-" and "-hedron". The latter comes from the Greek word hédra, which means "face of a geometrical solid". Overall it thus refers to the two faces of a polygon. Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetry, rotational symmetries and n reflection symmetry, reflection symmetries. Usually, we take n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice Of Subgroups
In mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial ordering being set inclusion. In this lattice, the join of two subgroups is the subgroup generated by their union, and the meet of two subgroups is their intersection. Example The dihedral group Dih4 has ten subgroups, counting itself and the trivial subgroup. Five of the eight group elements generate subgroups of order two, and the other two non- identity elements both generate the same cyclic subgroup of order four. In addition, there are two subgroups of the form Z2 × Z2, generated by pairs of elements. The lattice formed by these ten subgroups is shown in the illustration. This example also shows that the lattice of all subgroups of a group is not a modular lattice in general. Indeed, this particular lattice contains the forbidden "pentagon" N5 as a sublattice. Properties For any ''A'', ''B'', and ''C'' subgroups of a group with '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |