|
Model Collapse
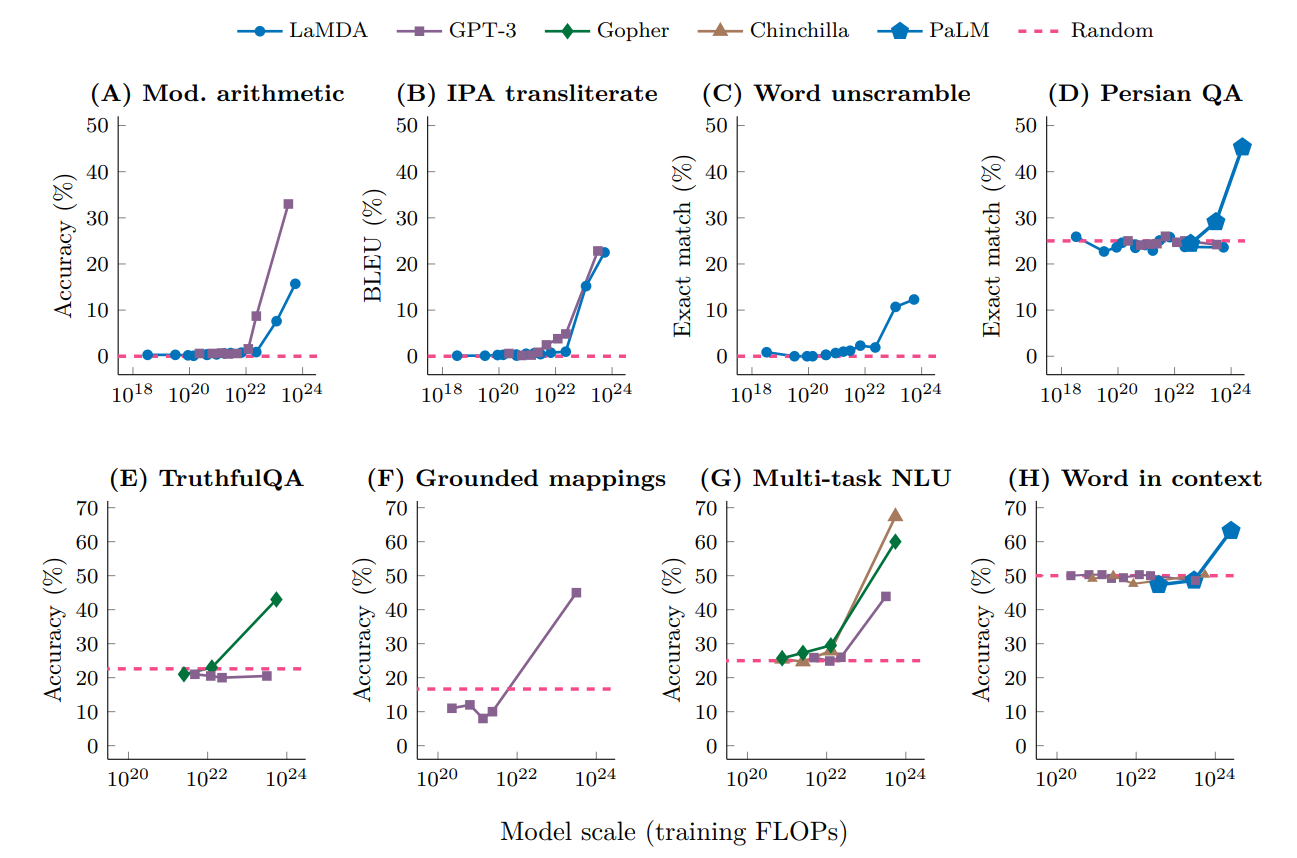
Model collapse is a phenomenon where machine learning models gradually degrade due to errors coming from uncurated training on the outputs of another model, such as prior versions of itself. Such outputs are known as synthetic data. It is a possible mechanism for mode collapse. Shumailov et al. coined the term and described two specific stages to the degradation: ''early model collapse'' and ''late model collapse'': * In early model collapse, the model begins losing information about the tails of the distribution – mostly affecting minority data. Later work highlighted that early model collapse is hard to notice, since overall performance may appear to improve, while the model loses performance on minority data. * In late model collapse, the model loses a significant proportion of its performance, confusing concepts and losing most of its variance. Mechanism Using synthetic data as training data can lead to issues with the quality and reliability of the trained model. Model c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inbreeding
Inbreeding is the production of offspring from the mating or breeding of individuals or organisms that are closely related genetically. By analogy, the term is used in human reproduction, but more commonly refers to the genetic disorders and other consequences that may arise from expression of deleterious or recessive traits resulting from incestuous sexual relationships and consanguinity. Animals avoid incest only rarely. Inbreeding results in homozygosity, which can increase the chances of offspring being affected by recessive traits. In extreme cases, this usually leads to at least temporarily decreased biological fitness of a population (called inbreeding depression), which is its ability to survive and reproduce. An individual who inherits such deleterious traits is colloquially referred to as ''inbred''. The avoidance of expression of such deleterious recessive alleles caused by inbreeding, via inbreeding avoidance mechanisms, is the main selective reason for ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance-gamma Distribution
The variance-gamma distribution, generalized Laplace distribution or Bessel function distribution is a continuous probability distribution that is defined as the normal variance-mean mixture where the mixing density is the gamma distribution. The tails of the distribution decrease more slowly than the normal distribution. It is therefore suitable to model phenomena where numerically large values are more probable than is the case for the normal distribution. Examples are returns from financial assets and turbulent wind speeds. The distribution was introduced in the financial literature by Madan and Seneta. The variance-gamma distributions form a subclass of the generalised hyperbolic distributions. The fact that there is a simple expression for the moment generating function implies that simple expressions for all moments are available. The class of variance-gamma distributions is closed under convolution in the following sense. If X_1 and X_2 are independent random variabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generation Loss
Generation loss is the loss of quality between subsequent copies or transcodes of data. Anything that reduces the quality of the representation when copying, and would cause further reduction in quality on making a copy of the copy, can be considered a form of generation loss. File size increases are a common result of generation loss, as the introduction of artifacts may actually increase the entropy of the data through each generation. Analog generation loss In analog systems (including systems that use digital recording but make the copy over an analog connection), generation loss is mostly due to noise and bandwidth issues in cables, amplifiers, mixers, recording equipment and anything else between the source and the destination. Poorly adjusted distribution amplifiers and mismatched impedances can make these problems even worse. Repeated conversion between analog and digital can also cause loss. Generation loss was a major consideration in complex analog audio and vid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Large Language Model
A large language model (LLM) is a language model consisting of a neural network with many parameters (typically billions of weights or more), trained on large quantities of unlabelled text using self-supervised learning. LLMs emerged around 2018 and perform well at a wide variety of tasks. This has shifted the focus of natural language processing research away from the previous paradigm of training specialized supervised models for specific tasks. Properties Though the term ''large language model'' has no formal definition, it often refers to deep learning models having a parameter count on the order of billions or more. LLMs are general purpose models which excel at a wide range of tasks, as opposed to being trained for one specific task (such as sentiment analysis, named entity recognition, or mathematical reasoning). The skill with which they accomplish tasks, and the range of tasks at which they are capable, seems to be a function of the amount of resources (data, parameter-si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Softmax
The softmax function, also known as softargmax or normalized exponential function, converts a vector of real numbers into a probability distribution of possible outcomes. It is a generalization of the logistic function to multiple dimensions, and used in multinomial logistic regression. The softmax function is often used as the last activation function of a neural network to normalize the output of a network to a probability distribution over predicted output classes, based on Luce's choice axiom. Definition The softmax function takes as input a vector of real numbers, and normalizes it into a probability distribution consisting of probabilities proportional to the exponentials of the input numbers. That is, prior to applying softmax, some vector components could be negative, or greater than one; and might not sum to 1; but after applying softmax, each component will be in the interval (0, 1), and the components will add up to 1, so that they can be interpreted as proba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four. Empirical examples The distributions of a wide variety of physical, biological, and man-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words in most languages, frequencies of family names, the species richness in clades of organisms, the sizes of power outages, volcanic eruptions, human judgments of stimulus intensity and many other quantit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables (also known as dependent and independent variables). The case of one explanatory variable is called '' simple linear regression''; for more than one, the process is called multiple linear regression. This term is distinct from multivariate linear regression, where multiple correlated dependent variables are predicted, rather than a single scalar variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimated from the data. Such models are called linear models. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, linear regressio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Empirical Risk Minimization
Empirical risk minimization (ERM) is a principle in statistical learning theory which defines a family of learning algorithms and is used to give theoretical bounds on their performance. The core idea is that we cannot know exactly how well an algorithm will work in practice (the true "risk") because we don't know the true distribution of data that the algorithm will work on, but we can instead measure its performance on a known set of training data (the "empirical" risk). Background Consider the following situation, which is a general setting of many supervised learning problems. We have two spaces of objects X and Y and would like to learn a function \ h: X \to Y (often called ''hypothesis'') which outputs an object y \in Y, given x \in X. To do so, we have at our disposal a ''training set'' of n examples \ (x_1, y_1), \ldots, (x_n, y_n) where x_i \in X is an input and y_i \in Y is the corresponding response that we wish to get from h(x_i). To put it more formally, we assu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wasserstein Distance
In mathematics, the Wasserstein distance or Kantorovich– Rubinstein metric is a distance function defined between probability distributions on a given metric space M. It is named after Leonid Vaseršteĭn. Intuitively, if each distribution is viewed as a unit amount of earth (soil) piled on ''M'', the metric is the minimum "cost" of turning one pile into the other, which is assumed to be the amount of earth that needs to be moved times the mean distance it has to be moved. This problem was first formalised by Gaspard Monge in 1781. Because of this analogy, the metric is known in computer science as the earth mover's distance. The name "Wasserstein distance" was coined by R. L. Dobrushin in 1970, after learning of it in the work of Leonid Vaseršteĭn on Markov processes describing large systems of automata (Russian, 1969). However the metric was first defined by Leonid Kantorovich in ''The Mathematical Method of Production Planning and Organization'' (Russian original 1939) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Walk
In mathematics, a random walk is a random process that describes a path that consists of a succession of random steps on some mathematical space. An elementary example of a random walk is the random walk on the integer number line \mathbb Z which starts at 0, and at each step moves +1 or −1 with equal probability. Other examples include the path traced by a molecule as it travels in a liquid or a gas (see Brownian motion), the search path of a foraging animal, or the price of a fluctuating stock and the financial status of a gambler. Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology, economics, and sociology. The term ''random walk'' was first introduced by Karl Pearson in 1905. Lattice random walk A popular random walk model is that of a random walk on a regular lattice, where at each step the location jumps to another site according to some probability distribution. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Distribution
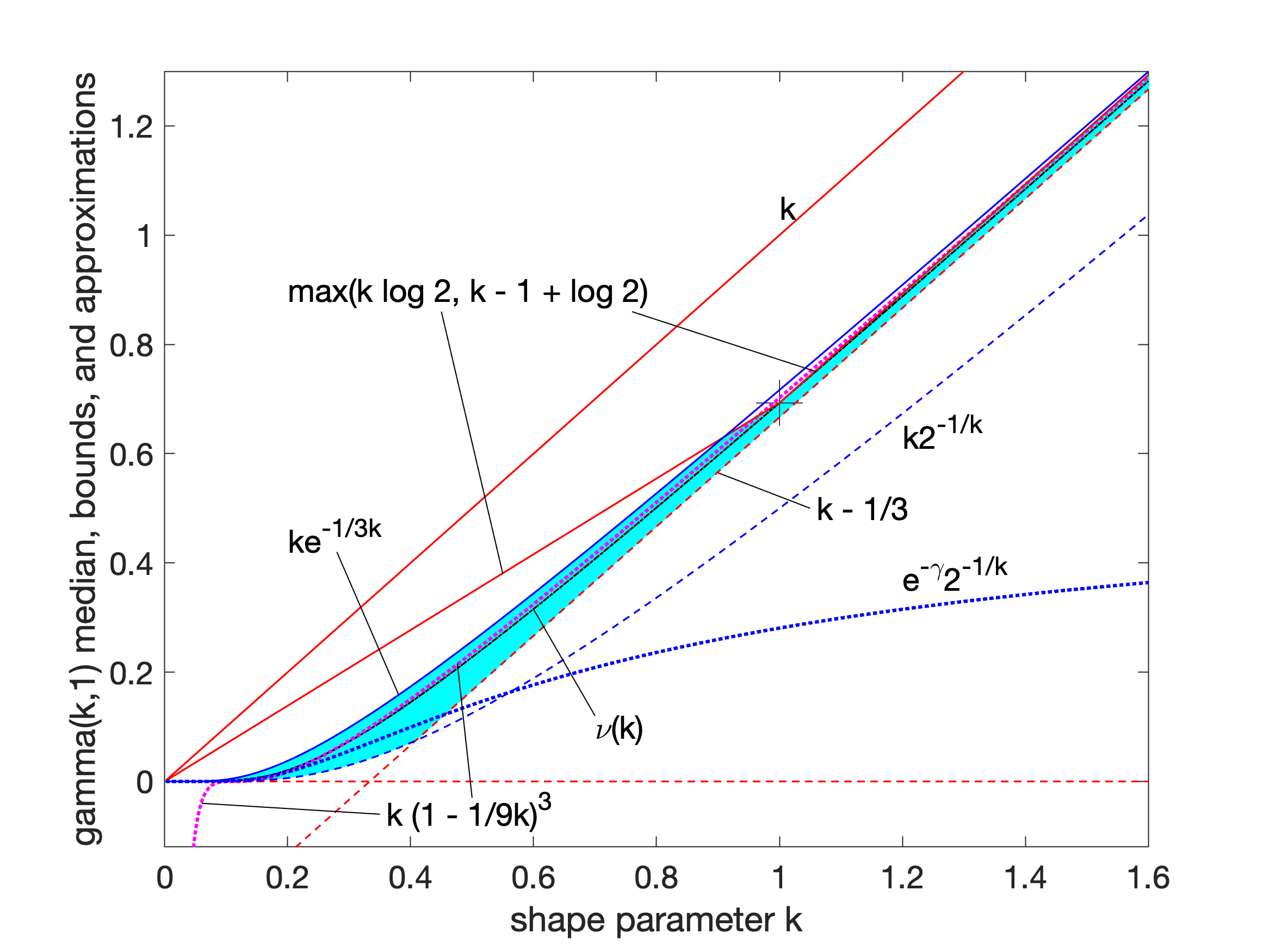
In probability theory and statistics, the gamma distribution is a two- parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-square distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: #With a shape parameter k and a scale parameter \theta. #With a shape parameter \alpha = k and an inverse scale parameter \beta = 1/ \theta , called a rate parameter. In each of these forms, both parameters are positive real numbers. The gamma distribution is the maximum entropy probability distribution (both with respect to a uniform base measure and a 1/x base measure) for a random variable X for which E 'X''= ''kθ'' = ''α''/''β'' is fixed and greater than zero, and E n(''X'')= ''ψ''(''k'') + ln(''θ'') = ''ψ''(''α'') − ln(''β'') is fixed (''ψ'' is the digamma function). Definitions The parameterization with ''k'' and ''θ'' appears to be more common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cochran's Theorem
In statistics, Cochran's theorem, devised by William G. Cochran, is a theorem used to justify results relating to the probability distributions of statistics that are used in the analysis of variance. Statement Let ''U''1, ..., ''U''''N'' be i.i.d. standard normally distributed random variables, and U = _1, ..., U_NT. Let B^,B^,\ldots, B^be symmetric matrices. Define ''r''''i'' to be the rank of B^. Define Q_i=U^T B^U, so that the ''Q''i are quadratic forms. Further assume \sum_i Q_i = U^T U. Cochran's theorem states that the following are equivalent: * r_1+\cdots +r_k=N, * the ''Q''''i'' are independent * each ''Q''''i'' has a chi-squared distribution with ''r''''i'' degrees of freedom. Often it's stated as \sum_i A_i = A, where A is idempotent, and \sum_i r_i = N is replaced by \sum_i r_i = rank(A). But after an orthogonal transform, A = diag(I_M, 0), and so we reduce to the above theorem. Proof Claim: Let X be a standard Gaussian in \R^n, then for any symmetric matric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)