|
Mean-periodic Function
In mathematical analysis, the concept of a mean-periodic function is a generalization introduced in 1935 by Jean Delsarte of the concept of a periodic function. Further results were made by Laurent Schwartz and J-P Kahane. Definition Consider a continuous complex number, complex-valued function of a real number, real variable. The function is periodic with period precisely if for all real , we have . This can be written as : \int f(x-t) \, d\mu(t) = 0\qquad\qquad(1) where \mu is the difference between the Dirac delta function, Dirac measures at 0 and ''a''. The function is mean-periodic if it satisfies the same equation (1), but where \mu is some arbitrary nonzero measure with compact (hence bounded) support. Equation (1) can be interpreted as a convolution, so that a mean-periodic function is a function for which there exists a compactly supported (signed) Borel measure \mu for which f*\mu = 0. There are several well-known equivalent definitions. Relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean Delsarte
Jean Frédéric Auguste Delsarte (19 October 1903, in Fourmies – 28 November 1968, in Nancy) was a French mathematician known for his work in mathematical analysis, in particular, for introducing mean-periodic functions and generalised shift operators. He was one of the founders of the Bourbaki group. He was an invited speaker at the International Congress of Mathematicians in 1932 at Zürich Zurich (; ) is the list of cities in Switzerland, largest city in Switzerland and the capital of the canton of Zurich. It is in north-central Switzerland, at the northwestern tip of Lake Zurich. , the municipality had 448,664 inhabitants. The .... Selected publications * * Application de la théorie des fonctions moyenne-périodiques à la résolution de certaines équations intégrales (1934) * Application de la théorie des fonctions moyenne-périodiques à la résolution des équations de Fredholm-Nörlund (1935) * * Fonctions moyenne-périodiques sur un groupe abstrait (193 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function that is not periodic is called ''aperiodic''. Definition A function is said to be periodic if, for some nonzero constant , it is the case that :f(x+P) = f(x) for all values of in the domain. A nonzero constant for which this is the case is called a period of the function. If there exists a least positive constant with this property, it is called the fundamental period (also primitive period, basic period, or prime period.) Often, "the" period of a function is used to mean its fundamental period. A funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Schwartz
Laurent-Moïse Schwartz (; 5 March 1915 – 4 July 2002) was a French mathematician. He pioneered the theory of Distribution (mathematics), distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields Medal in 1950 for his work on the theory of distributions. For several years he taught at the École polytechnique. Biography Family Laurent Schwartz came from a Jewish family of Alsace, Alsatian origin, with a strong scientific background: his father was a well-known surgeon, his uncle Robert Debré (who contributed to the creation of UNICEF) was a famous Pediatrics, pediatrician, and his great-uncle-in-law, Jacques Hadamard, was a famous mathematician. During his training at Lycée Louis-le-Grand to enter the École Normale Supérieure, he fell in love with Marie-Hélène Schwartz, Marie-Hélène Lévy, daughter of the probabilist Paul Lévy (mathematician), Paul Lévy who was then teaching at the École polytechniqu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature, "imaginary" complex numbers have a mathematical existence as firm as that of the real numbers, and they are fundamental tools in the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with real or complex coefficie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and in many other branches of mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers, sometimes called "the reals", is traditionally denoted by a bold , often using blackboard bold, . The adjective ''real'', used in the 17th century by René Descartes, distinguishes real numbers from imaginary numbers such as the square roots of . The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real numbers are called irrational numbers. Some irrational numbers (as well as all the rationals) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematical analysis, the Dirac delta function (or distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be Heuristic, represented heuristically as \delta (x) = \begin 0, & x \neq 0 \\ , & x = 0 \end such that \int_^ \delta(x) dx=1. Since there is no function having this property, modelling the delta "function" rigorously involves the use of limit (mathematics), limits or, as is common in mathematics, measure theory and the theory of distribution (mathematics), distributions. The delta function was introduced by physicist Paul Dirac, and has since been applied routinely in physics and engineering to model point masses and instantaneous impulses. It is called the delta function because it is a continuous analogue of the Kronecker delta function, which is usually defined on a discrete domain and takes values ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convolution
In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two functions after one is reflected about the y-axis and shifted. The term ''convolution'' refers to both the resulting function and to the process of computing it. The integral is evaluated for all values of shift, producing the convolution function. The choice of which function is reflected and shifted before the integral does not change the integral result (see #Properties, commutativity). Graphically, it expresses how the 'shape' of one function is modified by the other. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, convolution f*g differs from cross-correlation f \star g only in that either f(x) or g(x) is reflected about the y-axis in convolution; thus i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Periodic Function
In mathematics, an almost periodic function is, loosely speaking, a function of a real variable that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov, Hermann Weyl and Abram Samoilovitch Besicovitch, amongst others. There is also a notion of almost periodic functions on locally compact abelian groups, first studied by John von Neumann. Almost periodicity is a property of dynamical systems that appear to retrace their paths through phase space, but not exactly. An example would be a planetary system, with planets in orbits moving with periods that are not commensurable (i.e., with a period vector that is not proportional to a vector of integers). A theorem of Kronecker from diophantine approximation can be used to show that any particular configuration that occurs once, will recur to within any specified accuracy: if we wai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
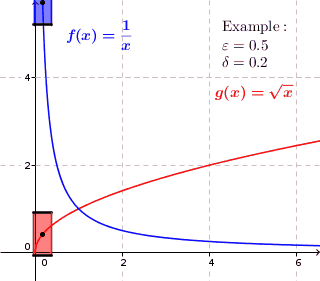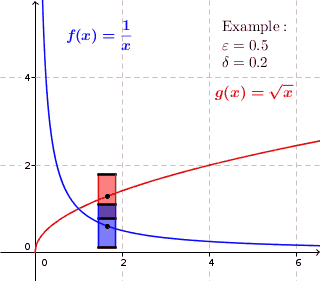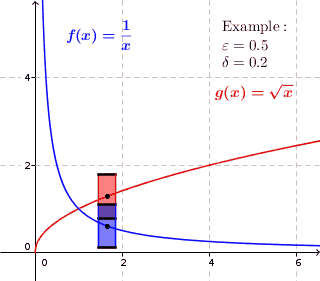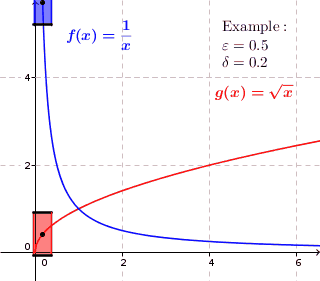
Uniformly Continuous
In mathematics, a real function f of real numbers is said to be uniformly continuous if there is a positive real number \delta such that function values over any function domain interval of the size \delta are as close to each other as we want. In other words, for a uniformly continuous real function of real numbers, if we want function value differences to be less than any positive real number \varepsilon, then there is a positive real number \delta such that , f(x) - f(y), 0 there exists a real number \delta > 0 such that for every x,y \in X with d_1(x,y) 0 such that for every x,y \in X , , x - y, 0 \; \forall x \in X \; \forall y \in X : \, d_1(x,y) 0 , \forall x \in X , and \forall y \in X ) are used. * Equivalently, f is uniformly continuous if it admits a modulus of continuity. Definition of (ordinary) continuity * f is called continuous \underline if for every real number \varepsilon > 0 there exists a real number \delta > 0 such that for every y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Langlands Correspondence
In mathematics, the Langlands program is a set of conjectures about connections between number theory, the theory of automorphic forms, and geometry. It was proposed by . It seeks to relate the structure of Galois groups in algebraic number theory to automorphic forms and, more generally, the representation theory of algebraic groups over local fields and adeles. It was described by Edward Frenkel as the "grand unified theory of mathematics." Background The Langlands program is built on existing ideas: the philosophy of cusp forms formulated a few years earlier by Harish-Chandra and , the work and Harish-Chandra's approach on semisimple Lie groups, and in technical terms the trace formula of Selberg and others. What was new in Langlands' work, besides technical depth, was the proposed connection to number theory, together with its rich organisational structure hypothesised (so-called functoriality). Harish-Chandra's work exploited the principle that what can be done for one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic Scheme
In mathematics, Arakelov theory (or Arakelov geometry) is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions. Background The main motivation behind Arakelov geometry is that there is a correspondence between prime ideals \mathfrak \in \text(\mathbb) and finite places v_p : \mathbb^* \to \mathbb, but there also exists a place at infinity v_\infty, given by the Archimedean valuation, which doesn't have a corresponding prime ideal. Arakelov geometry gives a technique for compactifying \text(\mathbb) into a complete space \overline which has a prime lying at infinity. Arakelov's original construction studies one such theory, where a definition of divisors is constructed for a scheme \mathfrak of relative dimension 1 over \text(\mathcal_K) such that it extends to a Riemann surface X_\infty = \mathfrak(\mathbb) for every valuation at infinity. In addition, he equips these Riemann surfaces with Hermitian metrics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |