|
Mathematical Puzzles
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions. Mathematical puzzles require mathematics to solve them. Logic puzzles are a common type of mathematical puzzle. Conway's Game of Life and fractals, as two examples, may also be considered mathematical puzzles even though the solver interacts with them only at the beginning by providing a set of initial conditions. After these conditions are set, the rules of the puzzle determine all subsequent changes and moves. Many of the puzzles are well known because they were discussed by Martin Gardner in his "Mathematical Games" column in Scientific American. Mathematical puzzles are sometimes used to motivate students in teaching elementary school math problem solving techniques.Kulkarni, DEnjoying Math: Learning Proble ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recreational Mathematics
Recreational mathematics is mathematics carried out for recreation (entertainment) rather than as a strictly research-and-application-based professional activity or as a part of a student's formal education. Although it is not necessarily limited to being an endeavor for amateurs, many topics in this field require no knowledge of advanced mathematics. Recreational mathematics involves mathematical puzzles and games, often appealing to children and untrained adults and inspiring their further study of the subject. The Mathematical Association of America (MAA) includes recreational mathematics as one of its seventeen Special Interest Groups, commenting: Mathematical competitions (such as those sponsored by mathematical associations) are also categorized under recreational mathematics. Topics Some of the more well-known topics in recreational mathematics are Rubik's Cubes, magic squares, fractals, logic puzzles and mathematical chess problems, but this area of mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
24 (puzzle)
The 24 puzzle is an arithmetical puzzle in which the objective is to find a way to manipulate four integers so that the end result is 24. For example, for the numbers 4, 7, 8, 8, a possible solution is (7-(8\div8))\times4=24. Note that all four numbers must be used exactly once. The problem has been played as a card game in Shanghai since the 1960s, using playing cards. It has been known by other names, including Maths24. A proprietary version of the game has been created which extends the concept of the basic game to more complex mathematical operations. Original version The original version of 24 is played with an ordinary deck of playing cards with all the face cards removed. The aces are taken to have the value 1 and the basic game proceeds by having 4 cards dealt and the first player that can achieve the number 24 exactly using only allowed operations (addition, subtraction, multiplication, Division (mathematics), division, and Order of operations, parentheses) wins the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
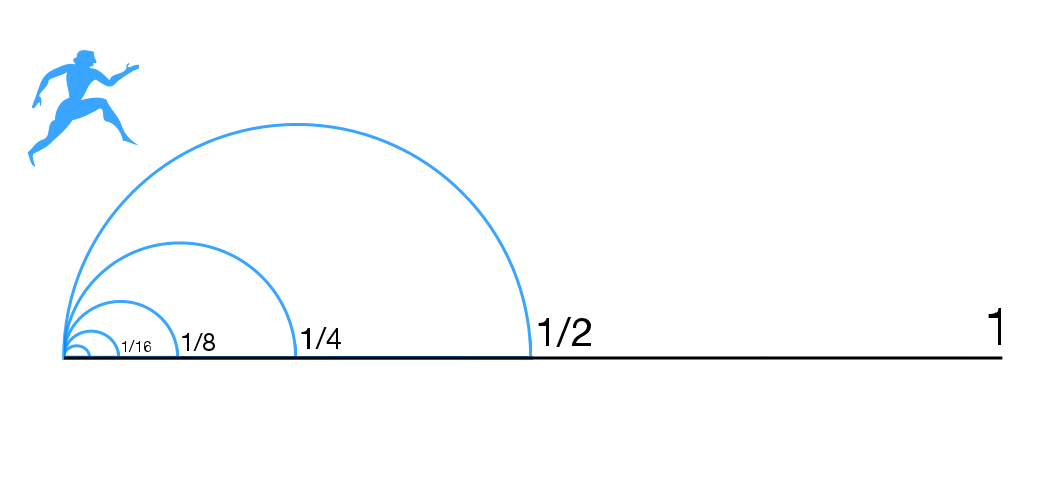
Zeno's Paradoxes
Zeno's paradoxes are a series of philosophical arguments presented by the ancient Greek philosopher Zeno of Elea (c. 490–430 BC), primarily known through the works of Plato, Aristotle, and later commentators like Simplicius of Cilicia. Zeno devised these paradoxes to support his teacher Parmenides's philosophy of monism, which posits that despite people's sensory experiences, reality is singular and unchanging. The paradoxes famously challenge the notions of plurality (the existence of many things), motion, space, and time by suggesting they lead to logical contradictions. Zeno's work, primarily known from second-hand accounts since his original texts are lost, comprises forty "paradoxes of plurality," which argue against the coherence of believing in multiple existences, and several arguments against motion and change. Of these, only a few are definitively known today, including the renowned "Achilles Paradox", which illustrates the problematic concept of infinite divisibi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ant On A Rubber Rope
The ant on a rubber rope is a mathematical puzzle with a solution that appears counterintuitive or paradoxical. It is sometimes given as a worm, or inchworm, on a rubber or elastic band, but the principles of the puzzle remain the same. The details of the puzzle can vary, but a typical form is as follows: At first consideration it seems that the ant will never reach the end of the rope, but whatever the length of the rope and the speeds, provided that the length and speeds remain steady, the ant will always be able to reach the end given sufficient time — in the form stated above, it would take years. There are two key principles: first, since the rubber rope is stretching both in front of and behind the ant, the proportion of the rope the ant has already walked is conserved, and, second, the proportional speed of the ant is inversely proportional to the length of the rubber rope, so the distance the ant can travel is unbounded like the harmonic series. A formal sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bridges Game
''Hashiwokakero'' (橋をかけろ ''Hashi o kakero''; lit. "build bridges!") is a type of logic puzzle published by Nikoli. It has also been published in English under the name ''Bridges'' or ''Chopsticks'' (based on a mistranslation: the ''hashi'' of the title, 橋, means ''bridge''; ''hashi'' written with another character, 箸, means ''chopsticks''). It has also appeared in ''The Times'' under the name ''Hashi''. In France, Denmark, the Netherlands, and Belgium it is published under the name Ai-Ki-Ai. Rules ''Hashiwokakero'' is played on a rectangular grid with no standard size, although the grid itself is not usually drawn. Some cells start out with (usually encircled) numbers from 1 to 8 inclusive; these are the "islands". The rest of the cells are empty. The goal is to connect all of the islands by drawing a series of bridges between the islands. The bridges must follow certain criteria:. * They must begin and end at distinct islands, travelling a straight line ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Think-a-Dot
The Think-a-Dot was a mathematical toy invented by Joseph Weisbecker and manufactured by E.S.R., Inc. during the 1960s that demonstrated automata theory. It had eight coloured disks on its front, and three holes on its top – left, right, and center – through which a ball bearing could be dropped. Each disk would display either a yellow or blue face, depending on whether the mechanism behind it was tipped to the right or the left. The Think-a-Dot thus had 28=256 internal states. When the ball fell to the bottom it would exit either to a hole on the left or the right of the device. As the ball passed through the Think-a-Dot, it would flip the disk mechanisms that it passed, and they in turn would determine whether the ball would be deflected to the left or to the right. Various puzzles and games were possible with the Think-a-Dot, such as flipping the colours of all cells in the minimum number of moves, or reaching a given state from a monochrome state or vice versa. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sujiko
Sujiko is a logic-based, combinatorial number-placement puzzle created by Jai Gomer of Kobayaashi Studios. The puzzle takes place on a 3x3 grid with four circled number clues at the centre of each quadrant which indicate the sum of the four numbers in that quadrant. The numbers 1-9 must be placed in the grid, in accordance with the circled clues, to complete the puzzle. Sujiko is featured in UK newspapers including ''The Times'', The Daily Telegraph, ''The Telegraph'', and The Sun (United Kingdom), ''The Sun''. References [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sudoku
Sudoku (; ; originally called Number Place) is a logic puzzle, logic-based, combinatorics, combinatorial number-placement puzzle. In classic Sudoku, the objective is to fill a 9 × 9 grid with digits so that each column, each row, and each of the nine 3 × 3 subgrids that compose the grid (also called "boxes", "blocks", or "regions") contains all of the digits from 1 to 9. The puzzle setter provides a partially completed grid, which for a well-posed problem, well-posed puzzle has a single solution. French newspapers featured similar puzzles in the 19th century, and the modern form of the puzzle first appeared in 1979 puzzle books by Dell Magazines under the name Number Place. However, the puzzle type only began to gain widespread popularity in 1986 when it was published by the Japanese puzzle company Nikoli (publisher), Nikoli under the name Sudoku, meaning "single number". In newspapers outside of Japan, it first appeared in ''The Conway Daily Sun'' (New Hamp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Str8ts
Str8ts is a logic-based number-placement puzzle, invented by Jeff Widderich in 2008. It is distinct from, but shares some properties and rules with, Sudoku. The name is derived from the poker straight. The puzzle is published in a number of newspapers internationally, in two book collections, and in downloadable apps. It was featured on the Canadian television show ''Dragons' Den'' on November 24, 2010. History A hand made prototype of Str8ts which used black cells and the new rule of straights in compartments was invented by Canadian puzzle designer Jeff Widderich in 2007. He approached Andrew Stuart, a UK-based puzzle maker and programmer, to make the puzzle. Their collaboration settled how the clues would be determined and finalized the rules. The first puzzle was presented at the Nuremberg International Toy Fair in February 2008. A daily puzzle has been published at their website since 24 November 2008, and more recently, a weekly "extreme" puzzle has appeared, which incorpo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanical Puzzle
A mechanical puzzle is a puzzle presented as a set of mechanically interlinked pieces in which the solution is to manipulate the whole object or parts of it. While puzzles of this type have been in use by humanity as early as the 3rd century BC, one of the most well-known mechanical puzzles of modern day is the Rubik's Cube, invented by the Hungarian architect Ernő Rubik in 1974. The puzzles are typically designed for a single player, where the goal is for the player to discover the principle of the object, rather than accidentally coming up with the right solution through trial and error. With this in mind, they are often used as an intelligence test or in problem solving training. History The oldest known mechanical puzzle comes from Greece and appeared in the 3rd century BC. The game consists of a square divided into 14 parts, and the aim was to create different shapes from these pieces. This is not easy to do. (see Ostomachion loculus Archimedius) In Iran "puzzle-locks" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |