|
Locally Finite Group
In mathematics, in the field of group theory, a locally finite group is a type of group that can be studied in ways analogous to a finite group. Sylow subgroups, Carter subgroups, and abelian subgroups of locally finite groups have been studied. The concept is credited to work in the 1930s by Russian mathematician Sergei Chernikov. Definition and first consequences A locally finite group is a group for which every finitely generated subgroup is finite. Since the cyclic subgroups of a locally finite group are finitely generated hence finite, every element has finite order, and so the group is periodic. Examples and non-examples Examples: * Every finite group is locally finite * Every infinite direct sum of finite groups is locally finite (Although the direct product may not be.) * Omega-categorical groups * The Prüfer groups are locally finite abelian groups * Every Hamiltonian group is locally finite * Every periodic solvable group is locally finite . * Every subgroup of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Group
In group theory, a Dedekind group is a group ''G'' such that every subgroup of ''G'' is normal. All abelian groups are Dedekind groups. A non-abelian Dedekind group is called a Hamiltonian group. The most familiar (and smallest) example of a Hamiltonian group is the quaternion group of order 8, denoted by Q8. Dedekind and Baer have shown (in the finite and respectively infinite order case) that every Hamiltonian group is a direct product of the form , where ''B'' is an elementary abelian 2-group, and ''D'' is a torsion abelian group with all elements of odd order. Dedekind groups are named after Richard Dedekind, who investigated them in , proving a form of the above structure theorem (for finite groups). He named the non-abelian ones after William Rowan Hamilton Sir William Rowan Hamilton LL.D, DCL, MRIA, FRAS (3/4 August 1805 – 2 September 1865) was an Irish mathematician, astronomer, and physicist. He was the Andrews Professor of Astronomy at Trinity College Dublin, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer-Verlag
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business international ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feit–Thompson Theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by . History conjectured that every nonabelian finite simple group has even order. suggested using the centralizers of involutions of simple groups as the basis for the classification of finite simple groups, as the Brauer–Fowler theorem shows that there are only a finite number of finite simple groups with given centralizer of an involution. A group of odd order has no involutions, so to carry out Brauer's program it is first necessary to show that non-cyclic finite simple groups never have odd order. This is equivalent to showing that odd order groups are solvable, which is what Feit and Thompson proved. The attack on Burnside's conjecture was started by , who studied CA groups; these are groups such that the Centralizer of every non-trivial element is Abelian. In a pioneering paper he showed that all CA groups of odd order ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip Hall
Philip Hall FRS (11 April 1904 – 30 December 1982), was an English mathematician. His major work was on group theory, notably on finite groups and solvable groups. Biography He was educated first at Christ's Hospital, where he won the Thompson Gold Medal for mathematics, and later at King's College, Cambridge. He was elected a Fellow of the Royal Society in 1951 and awarded its Sylvester Medal in 1961. He was President of the London Mathematical Society in 1955–1957, and awarded its Berwick Prize in 1958 and De Morgan Medal in 1965. Publications * * * See also * Abstract clone * Commutator collecting process * Isoclinism of groups * Regular p-group * Three subgroups lemma * Hall algebra, and Hall polynomials * Hall subgroup * Hall–Higman theorem * Hall–Littlewood polynomial * Hall's universal group * Hall's marriage theorem * Hall word * Hall–Witt identity * Irwin–Hall distribution * Zappa–Szép product In mathematics, especially group theory, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Abelian Group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel. The concept of an abelian group underlies many fundamental algebraic structures, such as fields, rings, vector spaces, and algebras. The theory of abelian groups is generally simpler than that of their non-abelian counterparts, and finite abelian groups are very well understood and fully classified. Definition An abelian group is a set A, together with an operation \cdot that combines any two elements a and b of A to form another element of A, denoted a \cdot b. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Burnside Problem
The Burnside problem asks whether a finitely generated group in which every element has finite order must necessarily be a finite group. It was posed by William Burnside in 1902, making it one of the oldest questions in group theory and was influential in the development of combinatorial group theory. It is known to have a negative answer in general, as Evgeny Golod and Igor Shafarevich provided a counter-example in 1964. The problem has many refinements and variants (see bounded and restricted below) that differ in the additional conditions imposed on the orders of the group elements, some of which are still open questions. Brief history Initial work pointed towards the affirmative answer. For example, if a group ''G'' is finitely generated and the order of each element of ''G'' is a divisor of 4, then ''G'' is finite. Moreover, A. I. Kostrikin was able to prove in 1958 that among the finite groups with a given number of generators and a given prime exponent, there exis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-group
In mathematics, specifically group theory, given a prime number ''p'', a ''p''-group is a group in which the order of every element is a power of ''p''. That is, for each element ''g'' of a ''p''-group ''G'', there exists a nonnegative integer ''n'' such that the product of ''pn'' copies of ''g'', and not fewer, is equal to the identity element. The orders of different elements may be different powers of ''p''. Abelian ''p''-groups are also called ''p''-primary or simply primary. A finite group is a ''p''-group if and only if its order (the number of its elements) is a power of ''p''. Given a finite group ''G'', the Sylow theorems guarantee the existence of a subgroup of ''G'' of order ''pn'' for every prime power ''pn'' that divides the order of ''G''. Every finite ''p''-group is nilpotent. The remainder of this article deals with finite ''p''-groups. For an example of an infinite abelian ''p''-group, see Prüfer group, and for an example of an infinite simple ''p' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sylow's Theorems
In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Peter Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains. The Sylow theorems form a fundamental part of finite group theory and have very important applications in the classification of finite simple groups. For a prime number p, a Sylow ''p''-subgroup (sometimes ''p''-Sylow subgroup) of a group G is a maximal p-subgroup of G, i.e., a subgroup of G that is a ''p''-group (meaning its cardinality is a power of p, or equivalently, the order of every group element is a power of p) that is not a proper subgroup of any other p-subgroup of G. The set of all Sylow p-subgroups for a given prime p is sometimes written \text_p(G). The Sylow theorems assert a partial converse to Lagrange's theorem. Lagrange's theorem states that for any finite group G the orde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
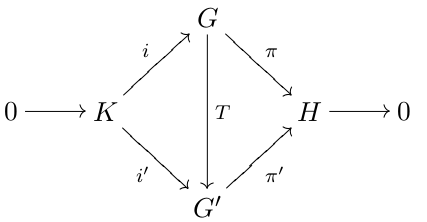
Group Extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence :1\to N\;\overset\;G\;\overset\;Q \to 1. If G is an extension of Q by N, then G is a group, \iota(N) is a normal subgroup of G and the quotient group G/\iota(N) is isomorphic to the group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined. Note that the phrasing "G is an extension of N by Q" is also used by some. Since any finite group G possesses a maximal normal subgroup N with simple factor group G/N, all finite groups may be constructed as a series of extensions with finite simple groups. This fact was a motivation for completing the classification of finite simple groups. An extension is called a central extension if the subgroup N lies in the cente ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quotient Group
A quotient group or factor group is a mathematical group obtained by aggregating similar elements of a larger group using an equivalence relation that preserves some of the group structure (the rest of the structure is "factored" out). For example, the cyclic group of addition modulo ''n'' can be obtained from the group of integers under addition by identifying elements that differ by a multiple of n and defining a group structure that operates on each such class (known as a congruence class) as a single entity. It is part of the mathematical field known as group theory. For a congruence relation on a group, the equivalence class of the identity element is always a normal subgroup of the original group, and the other equivalence classes are precisely the cosets of that normal subgroup. The resulting quotient is written G\,/\,N, where G is the original group and N is the normal subgroup. (This is pronounced G\bmod N, where \mbox is short for modulo.) Much of the importa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tarski Monster Group
In the area of modern algebra known as group theory, a Tarski monster group, named for Alfred Tarski, is an infinite group ''G'', such that every proper subgroup ''H'' of ''G'', other than the identity subgroup, is a cyclic group of order a fixed prime number ''p''. A Tarski monster group is necessarily simple. It was shown by Alexander Yu. Olshanskii in 1979 that Tarski groups exist, and that there is a Tarski ''p''-group for every prime ''p'' > 1075. They are a source of counterexamples to conjectures in group theory, most importantly to Burnside's problem and the von Neumann conjecture. Definition Let p be a fixed prime number. An infinite group G is called a Tarski monster group for p if every nontrivial subgroup (i.e. every subgroup other than 1 and G itself) has p elements. Properties * G is necessarily finitely generated. In fact it is generated by every two non-commuting elements. * G is simple. If N\trianglelefteq G and U\leq G is any subgroup distinct from N the su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |