|
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Segment Definition
Segment, segmentation, segmented, or segmental may refer to: Biology *Segmentation (biology), the division of body plans into a series of repetitive segments **Segmentation in the human nervous system *Internodal segment, the portion of a nerve fiber between two Nodes of Ranvier *Segment, in fruit anatomy, a section of a citrus fruit *Parts of a Genome#Viral genomes, genome, especially in virology Computing and communications *Episode#Segment (radio and television), Episode§Segment (radio and television), sub-unit of an episode of radio or television or podcast *Memory segmentation, the division of computer memory into segments **Segment descriptor **Data segment **Code segment *Image segmentation, the process of partitioning a digital image into multiple segments *Time-series segmentation, the process of partitioning a time-series into a sequence of discrete segments in order to reveal the underlying properties of its source *Network segmentation, splitting a computer network in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-dimensional Space
A one-dimensional space (1D space) is a mathematical space in which location can be specified with a single coordinate. An example is the number line, each point of which is described by a single real number. Any straight line or smooth curve is a one-dimensional space, regardless of the dimension of the ambient space in which the line or curve is embedded. Examples include the circle on a plane, or a parametric space curve. In physical space, a 1D subspace is called a "linear dimension" ( rectilinear or curvilinear), with units of length (e.g., metre). In algebraic geometry there are several structures that are one-dimensional spaces but are usually referred to by more specific terms. Any field K is a one-dimensional vector space over itself. The projective line over K, denoted \mathbf P^1(K), is a one-dimensional space. In particular, if the field is the complex numbers \mathbb, then the complex projective line \mathbf P^1(\mathbb) is one-dimensional with respect to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Subset
In mathematics, an open set is a generalization of an open interval in the real line. In a metric space (a set with a distance defined between every two points), an open set is a set that, with every point in it, contains all points of the metric space that are sufficiently near to (that is, all points whose distance to is less than some value depending on ). More generally, an open set is a member of a given collection of subsets of a given set, a collection that has the property of containing every union of its members, every finite intersection of its members, the empty set, and the whole set itself. A set in which such a collection is given is called a topological space, and the collection is called a topology. These conditions are very loose, and allow enormous flexibility in the choice of open sets. For example, ''every'' subset can be open (the discrete topology), or ''no'' subset can be open except the space itself and the empty set (the indiscrete topology). In pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Set
In geometry, topology, and related branches of mathematics, a closed set is a Set (mathematics), set whose complement (set theory), complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points. In a complete metric space, a closed set is a set which is Closure (mathematics), closed under the limit of a sequence, limit operation. This should not be confused with closed manifold. Sets that are both open and closed and are called clopen sets. Definition Given a topological space (X, \tau), the following statements are equivalent: # a set A \subseteq X is in X. # A^c = X \setminus A is an open subset of (X, \tau); that is, A^ \in \tau. # A is equal to its Closure (topology), closure in X. # A contains all of its limit points. # A contains all of its Boundary (topology), boundary points. An alternative characterization (mathematics), characterization of closed sets is available via sequences and Net (mathematics), net ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topological Vector Space
In mathematics, a topological vector space (also called a linear topological space and commonly abbreviated TVS or t.v.s.) is one of the basic structures investigated in functional analysis. A topological vector space is a vector space that is also a topological space with the property that the vector space operations (vector addition and scalar multiplication) are also continuous functions. Such a topology is called a and every topological vector space has a uniform topological structure, allowing a notion of uniform convergence and completeness. Some authors also require that the space is a Hausdorff space (although this article does not). One of the most widely studied categories of TVSs are locally convex topological vector spaces. This article focuses on TVSs that are not necessarily locally convex. Other well-known examples of TVSs include Banach spaces, Hilbert spaces and Sobolev spaces. Many topological vector spaces are spaces of functions, or linear operators ac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
In mathematics, a set is a collection of different things; the things are '' elements'' or ''members'' of the set and are typically mathematical objects: numbers, symbols, points in space, lines, other geometric shapes, variables, or other sets. A set may be finite or infinite. There is a unique set with no elements, called the empty set; a set with a single element is a singleton. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. Context Before the end of the 19th century, sets were not studied specifically, and were not clearly distinguished from sequences. Most mathematicians considered infinity as potentialmeaning that it is the result of an endless processand were reluctant to consider infinite sets, that is sets whose number of members is not a natural number. Specific ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-empty
In mathematics, the empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, while in other theories, its existence can be deduced. Many possible properties of sets are vacuously true for the empty set. Any set other than the empty set is called ''non-empty''. In some textbooks and popularizations, the empty set is referred to as the "null set". However, null set is a distinct notion within the context of measure theory, in which it describes a set of measure zero (which is not necessarily empty). Notation Common notations for the empty set include "", "\emptyset", and "∅". The latter two symbols were introduced by the Bourbaki group (specifically André Weil) in 1939, inspired by the letter Ø () in the Danish and Norwegian alphabets. In the past, "0" (the numeral zero) was occasionally used as a symbol fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Connected Set
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties that distinguish topological spaces. A subset of a topological space X is a if it is a connected space when viewed as a subspace of X. Some related but stronger conditions are path connected, simply connected, and n-connected. Another related notion is locally connected, which neither implies nor follows from connectedness. Formal definition A topological space X is said to be if it is the union of two disjoint non-empty open sets. Otherwise, X is said to be connected. A subset of a topological space is said to be connected if it is connected under its subspace topology. Some authors exclude the empty set (with its unique topology) as a connected space, but this article does not follow that practice. For a topological space X the fol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
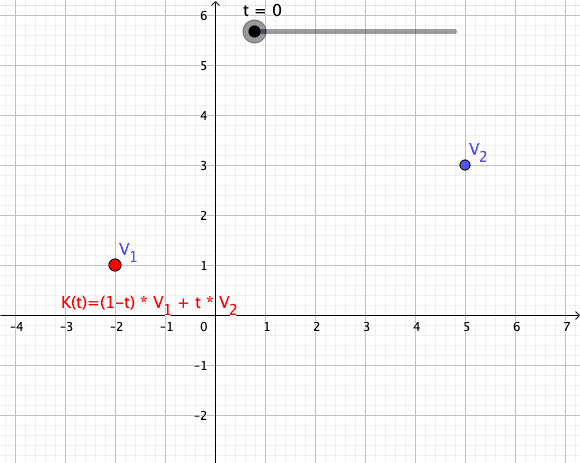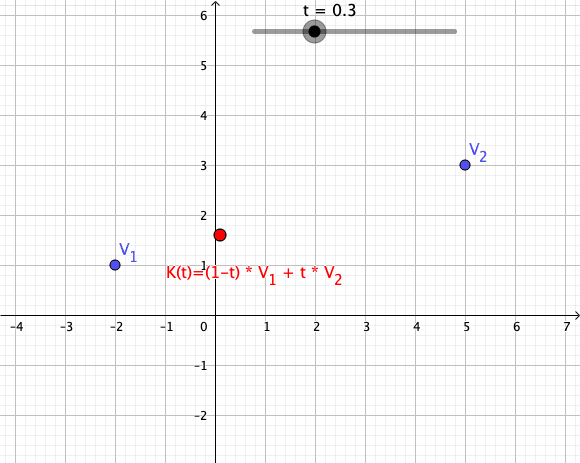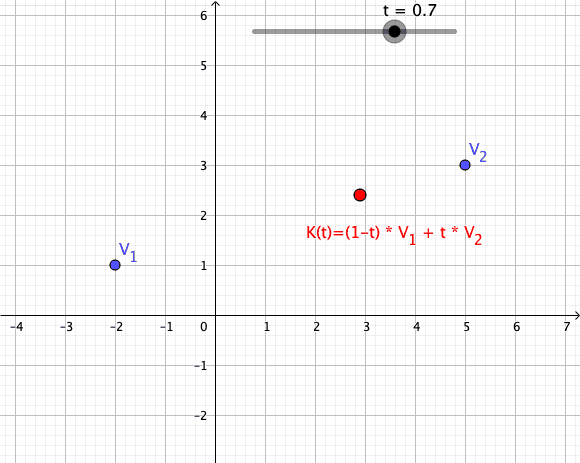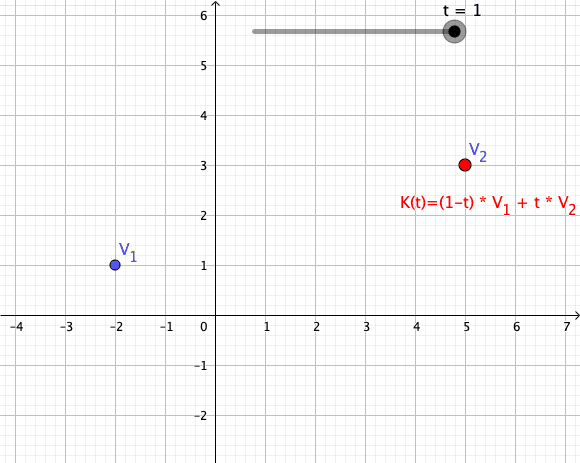
Convex Combination
In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. Formal definition More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex set, convex if it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a Bounded set, bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its projective duality, dual problem of intersecting Half-space (geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |