|
Linear Discriminant Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), canonical variates analysis (CVA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later statistical classification, classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical variable, categorical independent variables and a continuous variable, continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
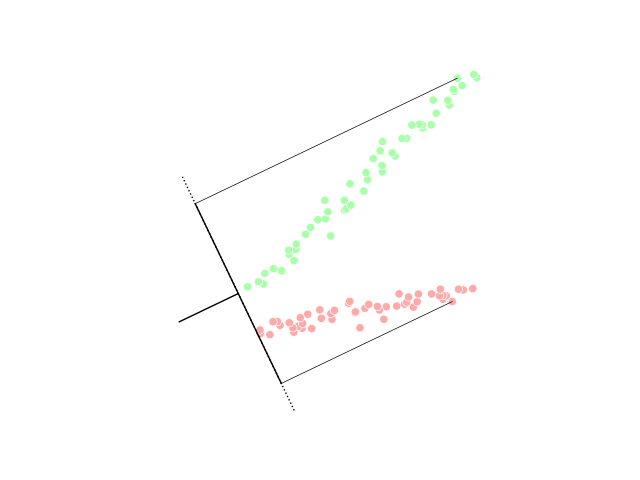
Linear Discriminant Analysis Plot
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a ''polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor (Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are ''nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that its degree ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Factor Analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus "error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models. Simply put, the factor loading of a variable quantifies the extent to which the variable is related to a given factor. A common rationale behind factor analytic methods is that the information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset. Factor analysis is commonly used in psychometrics, pers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quadratic Classifier
In statistics, a quadratic classifier is a statistical classifier that uses a quadratic decision surface to separate measurements of two or more classes of objects or events. It is a more general version of the linear classifier. The classification problem Statistical classification considers a set of vectors of observations of an object or event, each of which has a known type . This set is referred to as the training set. The problem is then to determine, for a given new observation vector, what the best class should be. For a quadratic classifier, the correct solution is assumed to be quadratic in the measurements, so will be decided based on \mathbf + \mathbf + c In the special case where each observation consists of two measurements, this means that the surfaces separating the classes will be conic sections (i.e., either a line, a circle or ellipse, a parabola or a hyperbola). In this sense, we can state that a quadratic model is a generalization of the linear model ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bayes Classifier
In statistical classification, the Bayes classifier is the classifier having the smallest probability of misclassification of all classifiers using the same set of features. Definition Suppose a pair (X,Y) takes values in \mathbb^d \times \, where Y is the class label of an element whose features are given by X. Assume that the conditional distribution of ''X'', given that the label ''Y'' takes the value ''r'' is given by (X\mid Y=r) \sim P_r \quad \text \quad r=1,2,\dots,K where "\sim" means "is distributed as", and where P_r denotes a probability distribution. A classifier is a rule that assigns to an observation ''X''=''x'' a guess or estimate of what the unobserved label ''Y''=''r'' actually was. In theoretical terms, a classifier is a measurable function C: \mathbb^d \to \, with the interpretation that ''C'' classifies the point ''x'' to the class ''C''(''x''). The probability of misclassification, or risk, of a classifier ''C'' is defined as \mathcal(C) = \operatorname\. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one variable mainly correspond with greater values of the other variable, and the same holds for lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when greater values of one variable mainly correspond to lesser values of the other (that is, the variables tend to show opposite behavior), the covariance is negative. The magnitude of the covariance is the geometric mean of the variances that are in common for the two random variables. The Pearson product-moment correlation coefficient, correlation coefficient normalizes the covariance by dividing by the geometric mean of the total variances for the two random variables. A distinction must be made between (1) the covariance of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables, each of which clusters around a mean value. Definitions Notation and parametrization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Supervised Learning
In machine learning, supervised learning (SL) is a paradigm where a Statistical model, model is trained using input objects (e.g. a vector of predictor variables) and desired output values (also known as a ''supervisory signal''), which are often human-made labels. The training process builds a function that maps new data to expected output values. An optimal scenario will allow for the algorithm to accurately determine output values for unseen instances. This requires the learning algorithm to Generalization (learning), generalize from the training data to unseen situations in a reasonable way (see inductive bias). This statistical quality of an algorithm is measured via a ''generalization error''. Steps to follow To solve a given problem of supervised learning, the following steps must be performed: # Determine the type of training samples. Before doing anything else, the user should decide what kind of data is to be used as a Training, validation, and test data sets, trainin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Training Set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from input data. These input data used to build the model are usually divided into multiple data sets. In particular, three data sets are commonly used in different stages of the creation of the model: training, validation, and test sets. The model is initially fit on a training data set, which is a set of examples used to fit the parameters (e.g. weights of connections between neurons in artificial neural networks) of the model. The model (e.g. a naive Bayes classifier) is trained on the training data set using a supervised learning method, for example using optimization methods such as gradient descent or stochastic gradient descent. In practice, the training data set often consists of pairs of an input vector (or scalar) and the correspondi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
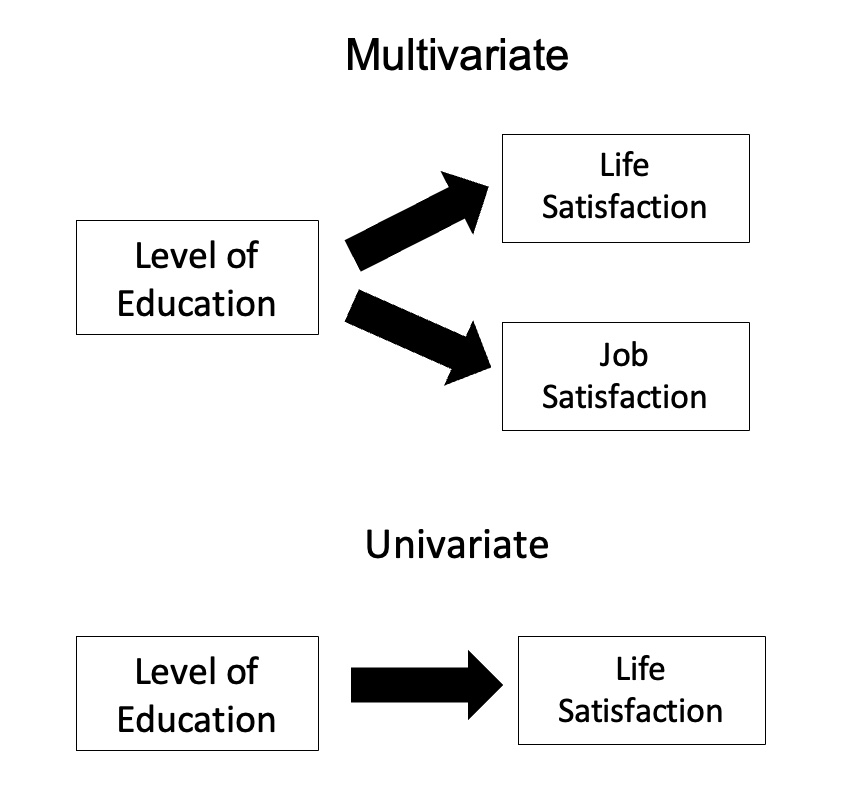
MANOVA
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately. Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers. Model Assume n q-dimensional observations, where the i’th observation y_i is assigned to the group g(i)\in \ and is distributed around the group center \mu^\in \mathbb R^q with multivariate Gaussian noise: y_i = \mu^ + \varepsilon_i\quad \varepsilon_i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
ANOVA
Analysis of variance (ANOVA) is a family of statistical methods used to compare the means of two or more groups by analyzing variance. Specifically, ANOVA compares the amount of variation ''between'' the group means to the amount of variation ''within'' each group. If the between-group variation is substantially larger than the within-group variation, it suggests that the group means are likely different. This comparison is done using an F-test. The underlying principle of ANOVA is based on the law of total variance, which states that the total variance in a dataset can be broken down into components attributable to different sources. In the case of ANOVA, these sources are the variation between groups and the variation within groups. ANOVA was developed by the statistician Ronald Fisher. In its simplest form, it provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. History While the analysis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, Fisher was the one to most comprehensively combine the ideas of Gregor Mendel and Charles Darwin, as his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the Modern synthesis (20th century), modern synthesis. For his contributions to biology, Richard Dawkins declared Fisher to be the greatest of Darwin's successors. He is also considered one of the founding fathers of Neo-Darwinism. According to statistician Jeffrey T. Leek, Fisher is the most in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |