Intermediate Value Theorem

picture info	Intermediate Value Theorem In mathematical analysis, the intermediate value theorem states that if f is a continuous function whose domain contains the interval , then it takes on any given value between f(a) and f(b) at some point within the interval. This has two important corollaries: # If a continuous function has values of opposite sign inside an interval, then it has a root in that interval (Bolzano's theorem). # The image of a continuous function over an interval is itself an interval. Motivation This captures an intuitive property of continuous functions over the real numbers: given ''f'' continuous on ,2/math> with the known values f(1) = 3 and f(2) = 5, then the graph of y = f(x) must pass through the horizontal line y = 4 while x moves from 1 to 2. It represents the idea that the graph of a continuous function on a closed interval can be drawn without lifting a pencil from the paper. Theorem The intermediate value theorem states the following: Consider the closed interval I = ,b/math> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
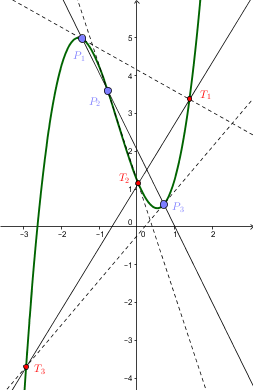
picture info	Illustration For The Intermediate Value Theorem An illustration is a decoration, interpretation, or visual explanation of a text, concept, or process, designed for integration in print and digitally published media, such as posters, Flyer (pamphlet), flyers, magazines, books, teaching materials, animations, video games and films. An illustration is typically created by an illustrator. Digital illustrations are often used to make websites and apps more user-friendly, such as the use of emojis to accompany digital type. Illustration also means providing an example; either in writing or in picture form. The origin of the word "illustration" is late Middle English (in the sense ‘illumination; spiritual or intellectual enlightenment’): via Old French from Latin ''illustratio''(n-), from the verb ''illustrare''. Illustration styles Contemporary illustration uses a wide range of styles and techniques, including drawing, painting, printmaking, collage, Photomontage, montage, Interaction design, digital design, multimedia, 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Weierstrass Nullstellensatz In mathematics, the Weierstrass Nullstellensatz is a version of the intermediate value theorem over a real closed field. It says: :Given a polynomial In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ... f in one variable with coefficients in a real closed field ''F'' and a < b in $F$ , if $f(a) < 0 < f(b)$ , then there exists a $c$ in $F$ such that $a < c < b$ and $f(c) = 0$ . Proof Since ''F'' is real-closed, ''F''(''i'') is algebraically closed, hence ''f''(''x'') can be written as $u\prod_i(x-\alpha_i)$ , where $u\in F$ is the leading coefficient and $\alpha_j\in F(i)$ are the roots of ''f''. Since each nonreal root $\alpha_j=a_j+ib_j$ can be paired ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Cubic Function In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. The derivative of a cubic function is a quadratic function. A cubic function with real coefficients has either one or three real roots ( which may not be distinct); all odd-degree polynomials with real coefficients have at least one real root. The graph of a cubic function always has a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Polynomial In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problem (mathematics education), word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Simon Stevin Simon Stevin (; 1548–1620), sometimes called Stevinus, was a County_of_Flanders, Flemish mathematician, scientist and music theorist. He made various contributions in many areas of science and engineering, both theoretical and practical. He also translated various mathematical terms into Dutch language, Dutch, making it one of the few European languages in which the word for mathematics, ''wikt:en:wiskunde#Dutch, wiskunde'' (''wikt:en:wis#Dutch, wis'' and ''wikt:en:kunde#Dutch, kunde'', i.e., "the knowledge of what is certain"), was not a loanword from Greek language, Greek but a calque via Latin. He also replaced the word ''wikt:en:chemie#Dutch, chemie'', the Dutch for chemistry, by ''wikt:en:scheikunde#Dutch, scheikunde'' ("the art of separating"), made in analogy#Linguistics, analogy with ''wikt:en:wiskunde#Dutch, wiskunde''. Biography Very little is known with certainty about Simon Stevin's life, and what we know is mostly inferred from other recorded facts.E. J. Dijkste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Joseph-Louis Lagrange Joseph-Louis Lagrange (born Giuseppe Luigi LagrangiaJoseph-Louis Lagrange, comte de l’Empire ''Encyclopædia Britannica'' or Giuseppe Ludovico De la Grange Tournier; 25 January 1736 – 10 April 1813), also reported as Giuseppe Luigi Lagrange or Lagrangia, was an Italian and naturalized French mathematician, physicist and astronomer. He made significant contributions to the fields of mathematical analysis, analysis, number theory, and both classical mechanics, classical and celestial mechanics. In 1766, on the recommendation of Leonhard Euler and Jean le Rond d'Alembert, d'Alembert, Lagrange succeeded Euler as the director of mathematics at the Prussian Academy of Sciences in Berlin, Prussia, where he stayed for over twenty y ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Augustin-Louis Cauchy Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real analysis), pioneered the field complex analysis, and the study of permutation groups in abstract algebra. Cauchy also contributed to a number of topics in mathematical physics, notably continuum mechanics. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: : "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific worker; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. Biography Youth and education Cauchy was the son of Lou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Constant Function In mathematics, a constant function is a function whose (output) value is the same for every input value. Basic properties As a real-valued function of a real-valued argument, a constant function has the general form or just For example, the function is the specific constant function where the output value is . The domain of this function is the set of all real numbers. The image of this function is the singleton set . The independent variable does not appear on the right side of the function expression and so its value is "vacuously substituted"; namely , , , and so on. No matter what value of is input, the output is . The graph of the constant function is a ''horizontal line'' in the plane that passes through the point . In the context of a polynomial in one variable , the constant function is called ''non-zero constant function'' because it is a polynomial of degree 0, and its general form is , where is nonzero. This function has no intersection point with the a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Bernard Bolzano Bernard Bolzano (, ; ; ; born Bernardus Placidus Johann Nepomuk Bolzano; 5 October 1781 – 18 December 1848) was a Bohemian mathematician, logician, philosopher, theologian and Catholic priest of Italian extraction, also known for his liberal views. Bolzano wrote in German, his native language. For the most part, his work came to prominence posthumously. Family Bolzano was the son of two pious Catholics. His father, Bernard Pompeius Bolzano, was an Italian who had moved to Prague, where he married Maria Cecilia Maurer who came from Prague's German-speaking family Maurer. Only two of their twelve children lived to adulthood. Career When he was ten years old, Bolzano entered the Gymnasium of the Piarists in Prague, which he attended from 1791 to 1796. Bolzano entered the University of Prague in 1796 and studied mathematics, philosophy and physics. Starting in 1800, he also began studying theology, becoming a Catholic priest in 1804. He was appointed to the new chair of p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Squaring The Circle Squaring the circle is a problem in geometry first proposed in Greek mathematics. It is the challenge of constructing a square (geometry), square with the area of a circle, area of a given circle by using only a finite number of steps with a compass and straightedge. The difficulty of the problem raised the question of whether specified axioms of Euclidean geometry concerning the existence of Line (geometry), lines and circles implied the existence of such a square. In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem, which proves that pi (\pi) is a transcendental number. That is, \pi is not the zero of a function, root of any polynomial with Rational number, rational coefficients. It had been known for decades that the construction would be impossible if \pi were transcendental, but that fact was not proven until 1882. Approximate constructions with any given non-perfect accuracy exist, and many such constructions have been f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Bryson Of Heraclea Bryson of Heraclea (, ''gen''.: Βρύσωνος; fl. late 5th-century BCE) was an ancient Greek mathematician and sophist who studied the solving the problems of squaring the circle and calculating pi. Life and work Little is known about the life of Bryson; he came from Heraclea Pontica, and he may have been a pupil of Socrates. He is mentioned in the '' 13th Platonic Epistle'', and Theopompus even claimed in his ''Attack upon Plato'' that Plato stole many ideas for his dialogues from Bryson of Heraclea. He is known principally from Aristotle, who criticizes his method of squaring the circle. He also upset Aristotle by asserting that obscene language does not exist. Diogenes Laërtius and the Suda refer several times to a Bryson as a teacher of various philosophers, but since some of the philosophers mentioned lived in the late 4th-century BCE, it is possible that Bryson became confused with Bryson of Achaea, who may have lived around that time. Pi and squaring the circle Bryso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Non-standard Analysis The history of calculus is fraught with philosophical debates about the meaning and logical validity of fluxions or infinitesimal numbers. The standard way to resolve these debates is to define the operations of calculus using (ε, δ)-definition of limit, limits rather than infinitesimals. Nonstandard analysis instead reformulates the calculus using a logically rigorous notion of infinitesimal numbers. Nonstandard analysis originated in the early 1960s by the mathematician Abraham Robinson. He wrote: ... the idea of infinitely small or ''infinitesimal'' quantities seems to appeal naturally to our intuition. At any rate, the use of infinitesimals was widespread during the formative stages of the Differential and Integral Calculus. As for the objection ... that the distance between two distinct real numbers cannot be infinitely small, Gottfried Wilhelm Leibniz argued that the theory of infinitesimals implies the introduction of ideal numbers which might be infinitely small or inf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]

Proof