|
Isoperimetric Ratio
In analytic geometry, the isoperimetric ratio of a simple closed curve in the Euclidean plane is the ratio , where is the length of the curve and is its area. It is a dimensionless quantity that is invariant under similarity transformations of the curve. According to the isoperimetric inequality, the isoperimetric ratio has its minimum value, 4, for a circle; any other curve has a larger value. Thus, the isoperimetric ratio can be used to measure how far from circular a shape is. The curve-shortening flow decreases the isoperimetric ratio of any smooth convex curve so that, in the limit as the curve shrinks to a point, the ratio becomes 4. For higher-dimensional bodies of dimension ''d'', the isoperimetric ratio can similarly be defined as where ''B'' is the surface area of the body (the measure of its boundary) and ''V'' is its volume (the measure of its interior). Other related quantities include the Cheeger constant of a Riemannian manifold In differential geometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytic Geometry
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry. Analytic geometry is used in physics and engineering, and also in aviation, Aerospace engineering, rocketry, space science, and spaceflight. It is the foundation of most modern fields of geometry, including Algebraic geometry, algebraic, Differential geometry, differential, Discrete geometry, discrete and computational geometry. Usually the Cartesian coordinate system is applied to manipulate equations for planes, straight lines, and circles, often in two and sometimes three dimensions. Geometrically, one studies the Euclidean plane (two dimensions) and Euclidean space. As taught in school books, analytic geometry can be explained more simply: it is concerned with defining and representing geometric shapes in a numerical way and extracting numerical information from shapes' numerical definitions and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
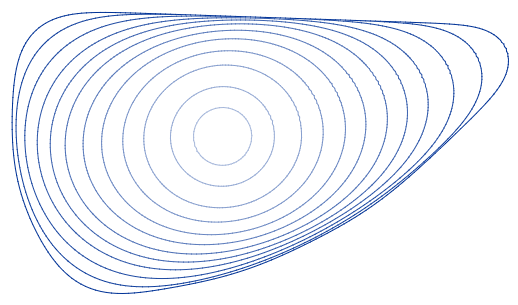
Curve-shortening Flow
In mathematics, the curve-shortening flow is a process that modifies a smooth curve in the Euclidean plane by moving its points perpendicularly to the curve at a speed proportional to the curvature. The curve-shortening flow is an example of a geometric flow, and is the one-dimensional case of the mean curvature flow. Other names for the same process include the Euclidean shortening flow, geometric heat flow, and arc length evolution. As the points of any smooth simple closed curve move in this way, the curve remains simple and smooth. It loses area at a constant rate, and its perimeter decreases as quickly as possible for any continuous curve evolution. If the curve is non-convex, its total absolute curvature decreases monotonically, until it becomes convex. Once convex, the isoperimetric ratio of the curve decreases as the curve converges to a circular shape, before collapsing to a singularity. If two disjoint simple smooth closed curves evolve, they remain disjoint until ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemannian Manifold
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the N-sphere, n-sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifold, manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them. Formally, a Riemannian metric (or just a metric) on a smooth manifold is a choice of inner product for each tangent space of the manifold. A Riemannian manifold is a smooth manifold together with a Riemannian metric. The techniques of differential and integral calculus are used to pull geometric data out of the Riemannian metric. For example, integration leads to the Riemannian distance function, whereas differentiation is used to define curvature and parallel transport. Any smooth surface in three-dimensional Eucl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cheeger Constant
In Riemannian geometry, the Cheeger isoperimetric constant of a compact Riemannian manifold ''M'' is a positive real number ''h''(''M'') defined in terms of the minimal area of a hypersurface that divides ''M'' into two disjoint pieces. In 1971, Jeff Cheeger proved an inequality that related the first nontrivial eigenvalue of the Laplace–Beltrami operator on ''M'' to ''h''(''M''). In 1982, Peter Buser proved a reverse version of this inequality, and the two inequalities put together are sometimes called the ''Cheeger-Buser inequality''. These inequalities were highly influential not only in Riemannian geometry and global analysis, but also in the theory of Markov chains and in graph theory, where they have inspired the analogous Cheeger constant of a graph and the notion of conductance. Definition Let ''M'' be an ''n''-dimensional closed Riemannian manifold. Let ''V''(''A'') denote the volume of an ''n''-dimensional submanifold ''A'' and ''S''(''E'') denote the ''n''&mi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume
Volume is a measure of regions in three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The definition of length and height (cubed) is interrelated with volume. The volume of a container is generally understood to be the capacity of the container; i.e., the amount of fluid (gas or liquid) that the container could hold, rather than the amount of space the container itself displaces. By metonymy, the term "volume" sometimes is used to refer to the corresponding region (e.g., bounding volume). In ancient times, volume was measured using similar-shaped natural containers. Later on, standardized containers were used. Some simple three-dimensional shapes can have their volume easily calculated using arithmetic formulas. Volumes of more complicated shapes can be calculated with integral calculus if a formula exists for the shape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Area
The surface area (symbol ''A'') of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc length of one-dimensional curves, or of the surface area for polyhedra (i.e., objects with flat polygonal faces), for which the surface area is the sum of the areas of its faces. Smooth surfaces, such as a sphere, are assigned surface area using their representation as parametric surfaces. This definition of surface area is based on methods of infinitesimal calculus and involves partial derivatives and double integration. A general definition of surface area was sought by Henri Lebesgue and Hermann Minkowski at the turn of the twentieth century. Their work led to the development of geometric measure theory, which studies various notions of surface area for irregular objects of any dimension. An important example is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inventiones Mathematicae
''Inventiones Mathematicae'' is a mathematical journal published monthly by Springer Science+Business Media. It was established in 1966 and is regarded as one of the most prestigious mathematics journals in the world. The current (2023) managing editors are Jean-Benoît Bost (University of Paris-Sud) and Wilhelm Schlag (Yale University Yale University is a Private university, private Ivy League research university in New Haven, Connecticut, United States. Founded in 1701, Yale is the List of Colonial Colleges, third-oldest institution of higher education in the United Stat ...). Abstracting and indexing The journal is abstracted and indexed in: References External links *{{Official website, https://www.springer.com/journal/222 Mathematics journals Academic journals established in 1966 English-language journals Springer Science+Business Media academic journals Monthly journals ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Curve
In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves (the boundaries of bounded convex sets), the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve. Bounded convex curves have a well-defined length, which can be obtained by approximating them with polygons, or from the average length of their projections onto a line. The maximum number of grid points that can belong to a single curve is controlled by its length. The points at which a convex curve has a unique supporting line are dense within the curve, and the distance of these lines fro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jordan Curve Theorem
In topology, the Jordan curve theorem (JCT), formulated by Camille Jordan in 1887, asserts that every ''Jordan curve'' (a plane simple closed curve) divides the plane into an "interior" region Boundary (topology), bounded by the curve (not to be confused with the interior (topology), interior of a set) and an "exterior" region containing all of the nearby and far away exterior points. Every path (topology), continuous path connecting a point of one region to a point of the other intersects with the curve somewhere. While the theorem seems intuitively obvious, it takes some ingenuity to prove it by elementary means. "Although the JCT is one of the best known topological theorems, there are many, even among professional mathematicians, who have never read a proof of it." (). More transparent proofs rely on the mathematical machinery of algebraic topology, and these lead to generalizations to higher-dimensional spaces. The Jordan curve theorem is named after the mathematician Camil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isoperimetric Inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. '' Isoperimetric'' literally means "having the same perimeter". Specifically, the isoperimetric inequality states, for the length ''L'' of a closed curve and the area ''A'' of the planar region that it encloses, that :4\pi A \le L^2, and that equality holds if and only if the curve is a circle. The isoperimetric problem is to determine a plane figure of the largest possible area whose boundary has a specified length. The closely related ''Dido's problem'' asks for a region of the maximal area bounded by a straight line and a curvilinear arc whose endpoints belong to that line. It is named after Dido, the legendary founder and first queen of Carthage. The solution to the isoperimetric problem is given by a circle and was known already in Ancient Greece. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Similarity (geometry)
In Euclidean geometry, two objects are similar if they have the same shape, or if one has the same shape as the mirror image of the other. More precisely, one can be obtained from the other by uniformly scaling (geometry), scaling (enlarging or reducing), possibly with additional translation (geometry), translation, rotation (mathematics), rotation and reflection (mathematics), reflection. This means that either object can be rescaled, repositioned, and reflected, so as to coincide precisely with the other object. If two objects are similar, each is congruence (geometry), congruent to the result of a particular uniform scaling of the other. For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. On the other hand, ellipses are not all similar to each other, rectangles are not all similar to each other, and isosceles triangles are not all similar to each other. This is because two ellipse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |