|
Isoelastic Function
In mathematical economics, an isoelastic function, sometimes constant elasticity function, is a function that exhibits a constant elasticity, i.e. has a constant elasticity coefficient. The elasticity is the ratio of the percentage change in the dependent variable to the percentage causative change in the independent variable, in the limit as the changes approach zero in magnitude. For an elasticity coefficient r (which can take on any real value), the function's general form is given by : f(x) = , where k and r are constants. The elasticity is by definition :\text = \frac \frac = \frac , which for this function simply equals ''r''. Derivation Elasticity of demand is indicated by = \frac \frac , where r is the elasticity, Q is quantity, and P is price. Rearranging gets us: \frac = \frac Then integrating \int\frac =\int \frac r \ln(P) + C = \ln(Q) Simplify e^ = e^ (e^)^re^C = Q kP^r = Q Q(P) = kP^r Examples Demand functions An example in mic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Economics
Mathematical economics is the application of Mathematics, mathematical methods to represent theories and analyze problems in economics. Often, these Applied mathematics#Economics, applied methods are beyond simple geometry, and may include differential and integral calculus, Recurrence relation, difference and differential equations, Matrix (mathematics), matrix algebra, mathematical programming, or other Computational economics, computational methods.TOC. Proponents of this approach claim that it allows the formulation of theoretical relationships with rigor, generality, and simplicity. Mathematics allows economists to form meaningful, testable propositions about wide-ranging and complex subjects which could less easily be expressed informally. Further, the language of mathematics allows economists to make specific, positiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
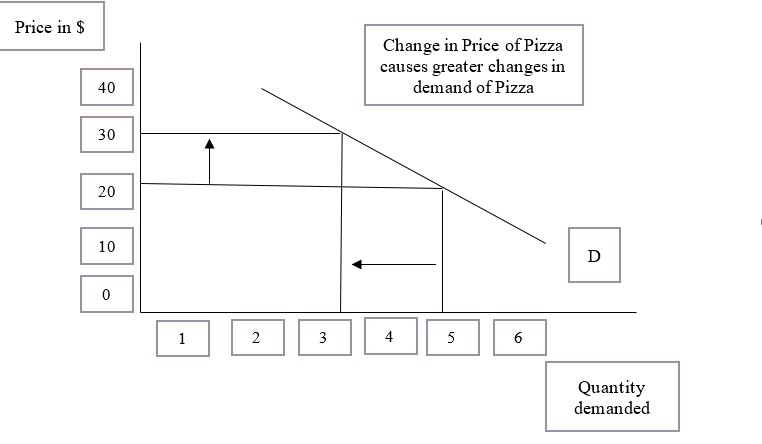
Elasticity (economics)
In economics, elasticity measures the responsiveness of one economic variable to a change in another. For example, if the price elasticity of the demand of a good is −2, then a 10% increase in price will cause the quantity demanded to fall by 20%. Elasticity in economics provides an understanding of changes in the behavior of the buyers and sellers with price changes. There are two types of elasticity for demand and supply, one is inelastic demand and supply and the other one is elastic demand and supply. Introduction The concept of price elasticity was first cited in an informal form in the book ''Principles of Economics (Marshall book), Principles of Economics'' published by the author Alfred Marshall in 1890. Subsequently, a major study of the price elasticity of supply and the price elasticity of demand for US products was undertaken by Joshua Levy and Trevor Pollock in the late 1960s. Elasticity is an important concept in neoclassical economic theory, and enables in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Coefficient
In chemistry, the Reaction rate, rate of a chemical reaction is influenced by many different factors, such as temperature, pH, reactant, the concentration of Product (chemistry), products, and other effectors. The degree to which these factors change the reaction rate is described by the elasticity coefficient. This coefficient is defined as follows: \varepsilon_^v = \left(\frac \frac\right)_ = \frac \approx \frac where v denotes the reaction rate and s denotes the Substrate (chemistry), substrate concentration. Be aware that the notation will use lowercase roman letters, such as s, to indicate concentrations. The partial derivative in the definition indicates that the elasticity is measured with respect to changes in a factor S while keeping all other factors constant. The most common factors include substrates, products, enzyme, and effectors. The scaling of the coefficient ensures that it is dimensionless and independent of the units used to measure the reaction rate and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dependent Variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the output is ; the functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Microeconomics
Microeconomics is a branch of economics that studies the behavior of individuals and Theory of the firm, firms in making decisions regarding the allocation of scarcity, scarce resources and the interactions among these individuals and firms. Microeconomics focuses on the study of individual markets, sectors, or industries as opposed to the economy as a whole, which is studied in macroeconomics. One goal of microeconomics is to analyze the market mechanisms that establish relative prices among goods and services and allocate limited resources among alternative uses. Microeconomics shows conditions under which free markets lead to desirable allocations. It also analyzes market failure, where markets fail to produce Economic efficiency, efficient results. While microeconomics focuses on firms and individuals, macroeconomics focuses on the total of economic activity, dealing with the issues of Economic growth, growth, inflation, and unemployment—and with national policies relati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Demand Curve
A demand curve is a graph depicting the inverse demand function, a relationship between the price of a certain commodity (the ''y''-axis) and the quantity of that commodity that is demanded at that price (the ''x''-axis). Demand curves can be used either for the price-quantity relationship for an individual consumer (an individual demand curve), or for all consumers in a particular market (a market demand curve). It is generally assumed that demand curves slope down, as shown in the adjacent image. This is because of the law of demand: for most goods, the quantity demanded falls if the price rises. Certain unusual situations do not follow this law. These include Veblen goods, Giffen goods, and speculative bubbles where buyers are attracted to a commodity if its price rises. Demand curves are used to estimate behaviour in competitive markets and are often combined with supply curves to find the equilibrium price (the price at which sellers together are willing to sell the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supply Curve
In economics, supply is the amount of a resource that firms, producers, labourers, providers of financial assets, or other economic agents are willing and able to provide to the marketplace or to an individual. Supply can be in produced goods, labour time, raw materials, or any other scarce or valuable object. Supply is often plotted graphically as a supply curve, with the price per unit on the vertical axis and quantity supplied as a function of price on the horizontal axis. This reversal of the usual position of the dependent variable and the independent variable is an unfortunate but standard convention. The supply curve can be either for an individual seller or for the market as a whole, adding up the quantity supplied by all sellers. The quantity supplied is for a particular time period (e.g., the tons of steel a firm would supply in a year), but the units and time are often omitted in theoretical presentations. In the goods market, supply is the amount of a product per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk Aversion
In economics and finance, risk aversion is the tendency of people to prefer outcomes with low uncertainty to those outcomes with high uncertainty, even if the average outcome of the latter is equal to or higher in monetary value than the more certain outcome. Risk aversion explains the inclination to agree to a situation with a lower average payoff that is more predictable rather than another situation with a less predictable payoff that is higher on average. For example, a risk-averse investor might choose to put their money into a bank account with a low but guaranteed interest rate, rather than into a stock that may have high expected returns, but also involves a chance of losing value. Example A person is given the choice between two scenarios: one with a guaranteed payoff, and one with a risky payoff with same average value. In the former scenario, the person receives $50. In the uncertain scenario, a coin is flipped to decide whether the person receives $100 or nothing. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concave Function
In mathematics, a concave function is one for which the function value at any convex combination of elements in the domain is greater than or equal to that convex combination of those domain elements. Equivalently, a concave function is any function for which the hypograph is convex. The class of concave functions is in a sense the opposite of the class of convex functions. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex. Definition A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be ''concave'' if, for any x and y in the interval and for any \alpha \in ,1/math>, :f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y) A function is called ''strictly concave'' if :f((1-\alpha )x+\alpha y) > (1-\alpha ) f(x)+\alpha f(y) for any \alpha \in (0,1) and x \neq y. For a function f: \mathbb \to \mathbb, this second definition merely states that for ev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Neumann-Morgenstern Utility Function
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational choice theory, a cornerstone of microeconomics, builds this postulate to model aggregate social behaviour. The expected utility hypothesis states an agent chooses between risky prospects by comparing expected utility values (i.e., the weighted sum of adding the respective utility values of payoffs multiplied by their probabilities). The summarised formula for expected utility is U(p)=\sum u(x_k)p_k where p_k is the probability that outcome indexed by k with payoff x_k is realized, and function ''u'' expresses the utility of each respective payoff. Graphically the curvature of the u function captures the agent's risk attitude. For example, imagine you’re offered a choice between receiving $50 for sure, or flipping a coin to win $100 if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isoelastic Utility
In economics, the isoelastic function for utility, also known as the isoelastic utility function, or power utility function, is used to express utility in terms of consumption or some other economic variable that a decision-maker is concerned with. The isoelastic utility function is a special case of hyperbolic absolute risk aversion and at the same time is the only class of utility functions with constant relative risk aversion, which is why it is also called the CRRA (constant relative risk aversion) utility function. In statistics, the same function is called the Box-Cox transformation. It is : u(c) = \begin \frac & \eta \ge 0, \eta \neq 1 \\ \ln(c) & \eta = 1 \end where c is consumption, u(c) the associated utility, and \eta is a constant that is positive for risk averse agents. Since additive constant terms in objective functions do not affect optimal decisions, the –1 is sometimes omitted in the numerator (although it should be kept if one wishes to preserve mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |