|
Inverse Dynamics
Inverse dynamics is an inverse problem. It commonly refers to either inverse rigid body dynamics or inverse structural dynamics. Inverse rigid-body dynamics is a method for computing forces and/or moments of force (torques) based on the kinematics (motion) of a body and the body's inertial properties (mass and moment of inertia). Typically it uses link-segment models to represent the mechanical behaviour of interconnected segments, such as the limbs of humans or animals or the joint extensions of robots, where given the kinematics of the various parts, inverse dynamics derives the minimum forces and moments responsible for the individual movements. In practice, inverse dynamics computes these internal moments and forces from measurements of the motion of limbs and external forces such as ground reaction forces, under a special set of assumptions.Robertson DGE, et al., Research Methods in Biomechanics, Champaign IL:Human Kinetics Pubs., 2004. Applications The fields of robotics an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects. Inverse problems are some of the most important mathematical problems in science and mathematics because they tell us about parameters that we cannot directly observe. They can be found in system identification, optics, radar, acoustics, communication theory, signal processing, medical imaging, computer vision, geophysics, oceanography, astronomy, remote sensing, natural language processing, machine learning, nondestructive testing, slope stability analys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newtonian Mechanics
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows: # A body remains at rest, or in motion at a constant speed in a straight line, unless it is acted upon by a force. # At any instant of time, the net force on a body is equal to the body's acceleration multiplied by its mass or, equivalently, the rate at which the body's momentum is changing with time. # If two bodies exert forces on each other, these forces have the same magnitude but opposite directions. The three laws of motion were first stated by Isaac Newton in his '' Philosophiæ Naturalis Principia Mathematica'' (''Mathematical Principles of Natural Philosophy''), originally published in 1687. Newton used them to investigate and explain the motion of many physical objects and systems. In the time since Newton, new insights, especially around ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Motor Control
Motor control is the regulation of movements in organisms that possess a nervous system. Motor control includes conscious voluntary movements, subconscious muscle memory and involuntary reflexes, as well as instinctual taxes. To control movement, the nervous system must integrate multimodal sensory information (both from the external world as well as proprioception) and elicit the necessary signals to recruit muscles to carry out a goal. This pathway spans many disciplines, including multisensory integration, signal processing, coordination, biomechanics, and cognition, and the computational challenges are often discussed under the term sensorimotor control. Successful motor control is crucial to interacting with the world to carry out goals as well as for posture, balance, and stability. Some researchers (mostly neuroscientists studying movement, such as Daniel Wolpert and Randy Flanagan) argue that motor control is the reason brains exist at all. Neural control ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robot Control
Robotic control is the system that contributes to the movement of robots. This involves the mechanical aspects and programmable systems that makes it possible to control robots. Robotics can be controlled by various means including manual, wireless, semi-autonomous (a mix of fully automatic and wireless control), and fully autonomous (using artificial intelligence). Modern robots (2000-present) Medical and surgical In the medical field, robots are used to make precise movements that are difficult for humans. Robotic surgery involves the use of less-invasive surgical methods, which are “procedures performed through tiny incisions”. Robots use the Da Vinci Surgical System, da Vinci surgical method, which involves the robotic arm (which holds onto surgical instruments) and a camera. The surgeon sits on a console where he controls the robot wirelessly. The feed from the camera is projected on a monitor, allowing the surgeon to see the incisions. The system is built to mimic t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Segment Parameter
Body may refer to: In science * Physical body, an object in physics that represents a large amount, has mass or takes up space * Body (biology), the physical material of an organism * Body plan, the physical features shared by a group of animals * Human body, the entire structure of a human organism ** Dead body, cadaver, or corpse, a dead human body * (living) matter, see: Mind–body problem, the relationship between mind and matter in philosophy * Aggregates within living matter, such as inclusion bodies In arts and entertainment In film and television * ''Jism'' (2003 film) or ''Body'', a 2003 Indian film * ''Body'' (2015 Polish film), a 2015 Polish film * ''Body'' (2015 American film), a 2015 American film * "Body" (''Wonder Showzen'' episode), a 2006 episode of American sketch comedy television series ''Wonder Showzen'' * "Body", an episode of the Adult Swim television series, ''Off the Air'' In literature and publishing * body text, the text forming the main content ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Kinematics
In computer animation and robotics, inverse kinematics is the mathematical process of calculating the variable joint parameters needed to place the end of a kinematic chain, such as a robot manipulator or animation character's skeleton, in a given position and orientation relative to the start of the chain. Given joint parameters, the position and orientation of the chain's end, e.g. the hand of the character or robot, can typically be calculated directly using multiple applications of trigonometric formulas, a process known as forward kinematics. However, the reverse operation is, in general, much more challenging. Inverse kinematics is also used to recover the movements of an object in the world from some other data, such as a film of those movements, or a film of the world as seen by a camera which is itself making those movements. This occurs, for example, where a human actor's filmed movements are to be duplicated by an animated character. Robotics In robotics, inverse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kinematics
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics. Kinematics is concerned with systems of specification of objects' positions and velocities and mathematical transformations between such systems. These systems may be rectangular like Cartesian coordinate system, cartesian, Curvilinear coordinates like polar coordinates or other systems. The object trajectories may be specified with respect to other objects which may themselve be in motion relative to a standard reference. Rotating systems may also be used. Numerous practical problems in kinematics involve constraints, such as mechanical linkages, ropes, or rolling disks. Overview Kinematics is a subfield of physics and mathematics, developed in classical mechanics, that describes the motion of points, Physical object, bodies (objects), and systems of bodies (group ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Of Revolution
In geometry, a solid of revolution is a Solid geometry, solid figure obtained by rotating a plane figure around some straight line (the ''axis of revolution''), which may not Intersection (geometry), intersect the generatrix (except at its boundary). The Surface (mathematics), surface created by this revolution and which bounds the solid is the ''surface of revolution''. Assuming that the curve does not cross the axis, the solid's volume is equal to the length of the circle described by the figure's centroid multiplied by the figure's area (Pappus's centroid theorem, Pappus's second centroid theorem). A representative disc is a three-dimensional volume element of a solid of revolution. The element is created by rotating a line segment (of length ) around some axis (located units away), so that a cylinder (geometry), cylindrical volume of units is enclosed. Finding the volume Two common methods for finding the volume of a solid of revolution are the Disc integration, disc met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Acceleration
In physics, angular acceleration (symbol α, alpha) is the time rate of change of angular velocity. Following the two types of angular velocity, ''spin angular velocity'' and ''orbital angular velocity'', the respective types of angular acceleration are: spin angular acceleration, involving a rigid body about an axis of rotation intersecting the body's centroid; and orbital angular acceleration, involving a point particle and an external axis. Angular acceleration has physical dimensions of angle per time squared, measured in SI units of radians per second squared (rads−2). In two dimensions, angular acceleration is a pseudoscalar whose sign is taken to be positive if the angular speed increases counterclockwise or decreases clockwise, and is taken to be negative if the angular speed increases clockwise or decreases counterclockwise. In three dimensions, angular acceleration is a pseudovector. Orbital angular acceleration of a point particle Particle in two dimensions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
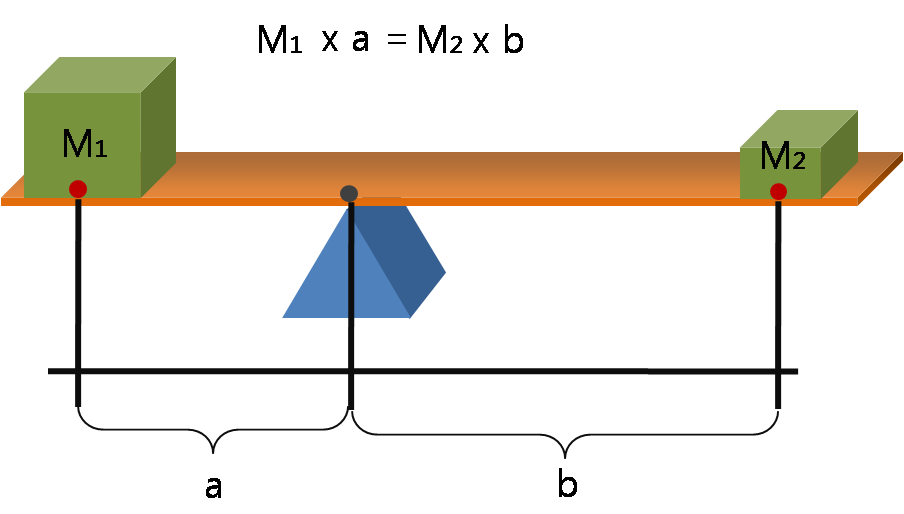
Moment (physics)
A moment is a mathematical expression involving the product of a distance and a physical quantity such as a force or electric charge. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions; a list of examples is provided later. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector quantities (in that they have Magnitude (mathematics), magnitude and Direction (geometry), direction). The orientation of an object's acceleration is given by the orientation of the ''net'' force acting on that object. The magnitude of an object's acceleration, as described by Newton's second law, is the combined effect of two causes: * the net balance of all external forces acting onto that object — magnitude is Direct proportionality, directly proportional to this net resulting force; * that object's mass, depending on the materials out of which it is made — magnitude is Inverse proportionality, inversely proportional to the object's mass. The International System of Units, SI unit for acceleration is metre per second squared (, \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties: * linearity of a '' function'' (or '' mapping''); * linearity of a '' polynomial''. An example of a linear function is the function defined by f(x)=(ax,bx) that maps the real line to a line in the Euclidean plane R2 that passes through the origin. An example of a linear polynomial in the variables X, Y and Z is aX+bY+cZ+d. Linearity of a mapping is closely related to '' proportionality''. Examples in physics include the linear relationship of voltage and current in an electrical conductor ( Ohm's law), and the relationship of mass and weight. By contrast, more complicated relationships, such as between velocity and kinetic energy, are '' nonlinear''. Generalized for functions in more than one dimension, linearity means the property of a function of being compatible with addition and scaling, also known as the superposition principle. Linearity of a polynomial means that its de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |