|
Harmonic Numbers
In mathematics, the -th harmonic number is the sum of the reciprocals of the first natural numbers: H_n= 1+\frac+\frac+\cdots+\frac =\sum_^n \frac. Starting from , the sequence of harmonic numbers begins: 1, \frac, \frac, \frac, \frac, \dots Harmonic numbers are related to the harmonic mean in that the -th harmonic number is also times the reciprocal of the harmonic mean of the first positive integers. Harmonic numbers have been studied since antiquity and are important in various branches of number theory. They are sometimes loosely termed harmonic series, are closely related to the Riemann zeta function, and appear in the expressions of various special functions. The harmonic numbers roughly approximate the natural logarithm function and thus the associated harmonic series grows without limit, albeit slowly. In 1737, Leonhard Euler used the divergence of the harmonic series to provide a new proof of the infinity of prime numbers. His work was extended into the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Numbers
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, and inde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Expansion
In mathematics, an asymptotic expansion, asymptotic series or Poincaré expansion (after Henri Poincaré) is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular, often infinite, point. Investigations by revealed that the divergent part of an asymptotic expansion is latently meaningful, i.e. contains information about the exact value of the expanded function. The most common type of asymptotic expansion is a power series in either positive or negative powers. Methods of generating such expansions include the Euler–Maclaurin summation formula and integral transforms such as the Laplace and Mellin transforms. Repeated integration by parts will often lead to an asymptotic expansion. Since a '' convergent'' Taylor series fits the definition of asymptotic expansion as well, the phrase "asymptotic series" usually implies a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
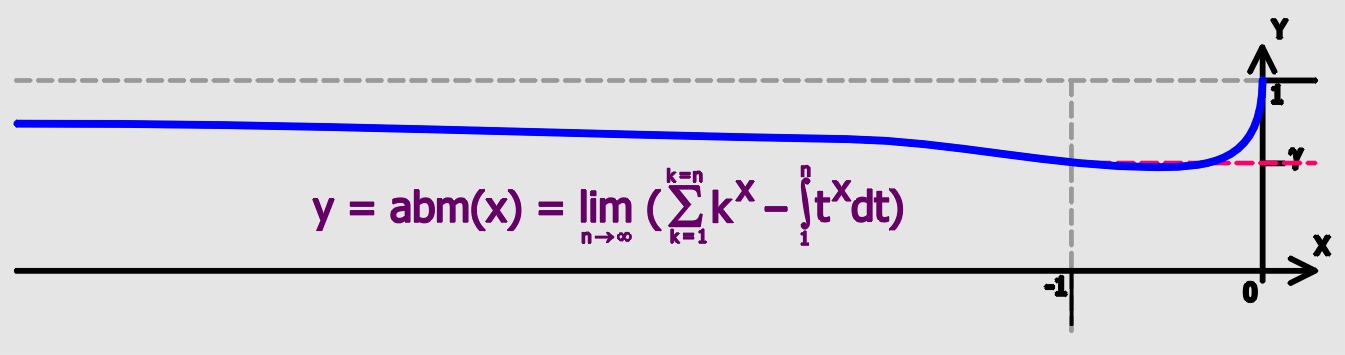
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Sequence
As the positive integer n becomes larger and larger, the value n\cdot \sin\left(\tfrac1\right) becomes arbitrarily close to 1. We say that "the limit of the sequence n\cdot \sin\left(\tfrac1\right) equals 1." In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the \lim symbol (e.g., \lim_a_n).Courant (1961), p. 29. If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests. Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers. History The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes. Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Test
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be interpreted as the signed area of the region in the plane that is bounded by the graph of a given function between two points in the real line. Conventionally, areas above the horizontal axis of the plane are positive while areas below are negative. Integrals also refer to the concept of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Identity
In mathematics, an identity is an equality relating one mathematical expression ''A'' to another mathematical expression ''B'', such that ''A'' and ''B'' (which might contain some variables) produce the same value for all values of the variables within a certain range of validity. In other words, ''A'' = ''B'' is an identity if ''A'' and ''B'' define the same functions, and an identity is an equality between functions that are differently defined. For example, (a+b)^2 = a^2 + 2ab + b^2 and \cos^2\theta + \sin^2\theta =1 are identities. Identities are sometimes indicated by the triple bar symbol instead of , the equals sign. Common identities Algebraic identities Certain identities, such as a+0=a and a+(-a)=0, form the basis of algebra, while other identities, such as (a+b)^2 = a^2 + 2ab +b^2 and a^2 - b^2 = (a+b)(a-b), can be useful in simplifying algebraic expressions and expanding them. Trigonometric identities Geometrically, trigonometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy and music theory. Euler is held to be one of the greatest mathematicians in history and the greatest of the 18th century. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss remarked: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." Euler ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stirling Numbers Of The First Kind
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles (counting fixed points as cycles of length one). The Stirling numbers of the first and second kind can be understood as inverses of one another when viewed as triangular matrices. This article is devoted to specifics of Stirling numbers of the first kind. Identities linking the two kinds appear in the article on Stirling numbers in general. Definitions The original definition of Stirling numbers of the first kind was algebraic: they are the coefficients s(n,k) in the expansion of the falling factorial :(x)_n = x(x-1)(x-2)\cdots(x-n+1) into powers of the variable x: :(x)_n = \sum_^n s(n,k) x^k, For example, (x)_3 = x(x-1)(x - 2) = 1x^3 - 3x^2 + 2x, leading to the values s(3, 3) = 1, s(3, 2) = -3, and s(3, 1) = 2. Subsequently, it was discovered that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Recurrence Relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter k that is independent of n; this number k is called the ''order'' of the relation. If the values of the first k numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation. In ''linear recurrences'', the th term is equated to a linear function of the k previous terms. A famous example is the recurrence for the Fibonacci numbers, F_n=F_+F_ where the order k is two and the linear function merely adds the two previous terms. This example is a linear recurrence with constant coefficients, because the coefficients of the linear function (1 and 1) are constants that do not depend on n. For these recurrences, one can express the general term of the sequence as a closed-form expression ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |