|
Hypercone
In geometry, a hypercone (or spherical cone) is the figure in the 4-dimensional Euclidean space represented by the equation :x^2 + y^2 + z^2 - w^2 = 0. It is a quadric surface, and is one of the possible 3-manifolds which are 4-dimensional equivalents of the conical surface in 3 dimensions. It is also named "spherical cone" because its intersections with hyperplanes perpendicular to the ''w''-axis are spheres. A four-dimensional right hypercone can be thought of as a sphere which expands with time, starting its expansion from a single point source, such that the center of the expanding sphere remains fixed. An oblique hypercone would be a sphere which expands with time, again starting its expansion from a point source, but such that the center of the expanding sphere moves with a uniform velocity. Parametric form A right spherical hypercone can be described by the function : \vec \sigma (\phi, \theta, t) = (t s \cos \theta \cos \phi, t s \cos \theta \sin \phi, t s \sin \theta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Light Cone
In special and general relativity, a light cone (or "null cone") is the path that a flash of light, emanating from a single Event (relativity), event (localized to a single point in space and a single moment in time) and traveling in all directions, would take through spacetime. Details If one imagines the light confined to a two-dimensional plane, the light from the flash spreads out in a circle after the event E occurs, and if we graph the growing circle with the vertical axis of the graph representing time, the result is a Cone (geometry), cone, known as the future light cone. The past light cone behaves like the future light cone in reverse, a circle which contracts in radius at the speed of light until it converges to a point at the exact position and time of the event E. In reality, there are three space Dimension (vector space), dimensions, so the light would actually form an expanding or contracting sphere in three-dimensional (3D) space rather than a circle in 2D, and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
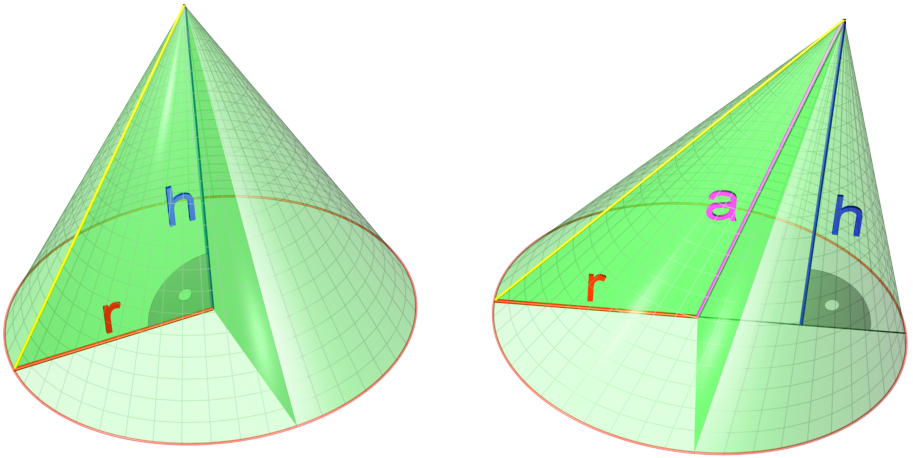
Cone (geometry)
In geometry, a cone is a three-dimensional figure that tapers smoothly from a flat base (typically a circle) to a point not contained in the base, called the '' apex'' or '' vertex''. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base. In the case of line segments, the cone does not extend beyond the base, while in the case of half-lines, it extends infinitely far. In the case of lines, the cone extends infinitely far in both directions from the apex, in which case it is sometimes called a ''double cone''. Each of the two halves of a double cone split at the apex is called a ''nappe''. Depending on the author, the base may be restricted to a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is an open surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Spherical Cone Lines
A sphere (from Greek , ) is a surface analogous to the circle, a curve. In solid geometry, a sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Basic terminology As mentioned earlier is t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Coordinate Time
In the theory of relativity, it is convenient to express results in terms of a spacetime coordinate system relative to an implied observer. In many (but not all) coordinate systems, an event is specified by one time coordinate and three spatial coordinates. The time specified by the time coordinate is referred to as coordinate time to distinguish it from proper time. In the special case of an inertial observer in special relativity, by convention the coordinate time at an event is the same as the proper time measured by a clock that is at the same location as the event, that is stationary relative to the observer and that has been synchronised to the observer's clock using the Einstein synchronisation convention. Coordinate time, proper time, and clock synchronization A fuller explanation of the concept of coordinate time arises from its relations with proper time and with clock synchronization. Synchronization, along with the related concept of simultaneity, has to recei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Four-dimensional Geometry
Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, called ''dimensions'', to describe the sizes or locations of objects in the everyday world. This concept of ordinary space is called Euclidean space because it corresponds to Euclid 's geometry, which was originally abstracted from the spatial experiences of everyday life. Single locations in Euclidean 4D space can be given as vectors or '' 4-tuples'', i.e., as ordered lists of numbers such as . For example, the volume of a rectangular box is found by measuring and multiplying its length, width, and height (often labeled , , and ). It is only when such locations are linked together into more complicated shapes that the full richness and geometric complexity of 4D spaces emerge. A hint of that complexity can be seen in the accompanying 2D animation of one of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a Neighbourhood (mathematics), neighborhood that is homeomorphic to an open (topology), open subset of n-dimensional Euclidean space. One-dimensional manifolds include Line (geometry), lines and circles, but not Lemniscate, self-crossing curves such as a figure 8. Two-dimensional manifolds are also called Surface (topology), surfaces. Examples include the Plane (geometry), plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hypersurface
In geometry, a hypersurface is a generalization of the concepts of hyperplane, plane curve, and surface. A hypersurface is a manifold or an algebraic variety of dimension , which is embedded in an ambient space of dimension , generally a Euclidean space, an affine space or a projective space. Hypersurfaces share, with surfaces in a three-dimensional space, the property of being defined by a single implicit equation, at least locally (near every point), and sometimes globally. A hypersurface in a (Euclidean, affine, or projective) space of dimension two is a plane curve. In a space of dimension three, it is a surface. For example, the equation :x_1^2+x_2^2+\cdots+x_n^2-1=0 defines an algebraic hypersurface of dimension in the Euclidean space of dimension . This hypersurface is also a smooth manifold, and is called a hypersphere or an -sphere. Smooth hypersurface A hypersurface that is a smooth manifold is called a ''smooth hypersurface''. In , a smooth hypersurface is ori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is one less than that of the ambient space. Two lower-dimensional examples of hyperplanes are one-dimensional lines in a plane and zero-dimensional points on a line. Most commonly, the ambient space is -dimensional Euclidean space, in which case the hyperplanes are the -dimensional "flats", each of which separates the space into two half spaces. A reflection across a hyperplane is a kind of motion ( geometric transformation preserving distance between points), and the group of all motions is generated by the reflections. A convex polytope is the intersection of half-spaces. In non-Euclidean geometry, the ambient space might be the -dimensional sphere or hyperbolic space, or more generally a pseudo-Riemannian space form, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior of a 3-sphere is a 4-ball. It is called a 3-sphere because topologically, the surface itself is 3-dimensional, even though it is curved into the 4th dimension. For example, when traveling on a 3-sphere, you can go north and south, east and west, or along a 3rd set of cardinal directions. This means that a 3-sphere is an example of a 3-manifold. Definition In coordinates, a 3-sphere with center and radius is the set of all points in real, Four-dimensional space, 4-dimensional space () such that :\sum_^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2. The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted : :S^3 = \left\. It is often convenient to r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rita G
Rita may refer to: People * Rita (given name) * Rita (Indian singer) (born 1984) * Rita (Israeli singer) (born 1962) * Rita (Japanese singer) * Eliza Humphreys (1850–1938), wrote under the pseudonym Rita Places * Djarrit, also known as Rita, a community in the Marshall Islands * 1180 Rita, an asteroid * Rita, West Virginia * Santa Rita, California (other), several places Film, television, and theater * ''Rita'' (1959 film), an Australian television play * ''Rita'' (2009 Italian film), an Italian film * ''Rita'' (2009 Indian film), a Marathi film directed by Renuka Shahane * ''Rita'' (2024 Guatemalan film), Guatemalan dark fantasy film * ''Rita'' (2024 Spanish film), an upcoming Spanish drama film * ''Rita'' (TV series), a Danish television show * RITA Award, an award for romantic fiction * '' Educating Rita'', a 1980 stage play by Willy Russel ** ''Educating Rita'' (film), a 1983 British film based on that play *Rita Oberoi, fictional character in the 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |